First off, congratulations to Dennis for making the Hall of Fame finalist list for 2011. The circumstances seem favorable to his making it, and if I had to guess I’d say he probably will. While his under-appreciated status has been a useful vehicle for my analytical agenda, I certainly hope he will be voted in—though I might prefer it be with a copy of my series in the voters’ hands.
Second, I apologize for the delay in getting this section out. I’m reminded of the words of the always brilliant Detective Columbo:
I worry. I mean, little things bother me. I’m a worrier. I mean, little insignificant details – I lose my appetite. I can’t eat. My wife, she says to me, “You know, you can really be a pain.”
Of course, as Columbo understood, the “insignificant” details that nag at you are usually anything but. Since Part 3 of this series should be the last to include heavily-quantitative analysis—and because it is so important to understanding Rodman’s true value—I really tried to tie up all the loose ends (even those that might at first seem to be redundant or obvious).
As a result, what began as a simple observation grew into something painfully detailed and extremely long (even by my standards)—but well worth it. So, once again, I’ve decided to break it down into 4 sections—however, each of these will be relatively short, and I’ll be posting them back-to-back each morning from now through Saturday. Here is the Cliff’s Notes version:
- Rodman had an observably great impact on his teams’ winning percentages.
- This impact was much greater than his already great impact on Margin of Victory would have predicted.
- Contrary to certain wisdom in the analytical community, Margin of Victory and Win% are both valuable indicators predictively, and combining Rodman’s differentials in both put him deep in Hall of Fame territory.
- Rodman’s differentials are statistically significant at one of the highest levels in NBA history.
Now, on with the show:
Introduction
One of the most common doubts I hear about Dennis Rodman’s value stems from the belief that his personal successes—5 NBA championships, freakish rebounding statistics, etc.—were probably largely a result of his having played for superior teams. For example, his prodigious rebounding may have been something he was “allowed” to do because he played for good offensive teams and (as the argument goes) had few other offensive responsibilities.
In it’s weaker form, I think this argument is plausible but irrelevant: Perhaps Rodman would not have been able to put up the numbers that he did if he were “required” to do more on offense. But the implication that this diminishes his value is absurd—it would be like saying that Cy Young wasn’t a particularly valuable baseball player because he couldn’t have put up such a great ERA if he were “required” to hit every night.
The stronger form, however, suggests that Rodman’s anomalous rebounding statistics probably weren’t due to any particularly anomalous talent or contribution, but were merely (or at least mostly) a byproduct of his fortunate circumstances.
If this were true, however, one of the following things would necessarily have to follow:
- His rebounding must not have contributed much value to his teams, or
- The situations he played in must have been uniquely favorable to leveraging value from a designated rebounder, or
- The choice to use a designated rebounder on an offensively strong team must have been an extremely successful exploitative strategy.
The third, I technically cannot disprove: It is theoretically possible that Rodman’s refusal to take a lot of shots on offense unintentionally caused his teams to stumble upon an amazing exploitative strategy that no one had discovered before and that no-one has duplicated since (though, if that were the case, he still might deserve some credit for forcing their hands).
But 1 and 2 simply aren’t supported by the data: As I will show, Rodman had wildly positive impacts on 4 different teams that had little in common, except of course for being solid winners with Rodman in the lineup.
Rodman’s Win % Differential
As I’ve discussed previously, a player’s differential statistics are simply the difference in their team’s performance in the games they played versus the games they missed. One very important differential stat we might be interested in is winning percentage.
To look at Rodman’s numbers in this area, I used exactly the same process that I described in Part 2(b) to look at his other differentials. However, for comparison purposes, I’ve greatly expanded the pool of players by dropping the qualifying minutes requirement from 3000 to 1000. This grows the pool from 164 players to 470.
Why expand? Honestly, because Rodman’s extreme win % differential allows it. I think the more stringent filters produce a list that is more reliable from top to bottom—but in this case, I am mostly interested in (literally) the top. There are some players on the list with barely 1/3 of a season’s worth of qualifying playing time to back up their numbers—which should produce extreme volatility—yet still no one is able to overtake Rodman.
Here is Rodman’s raw win differential, along with those of a number of select players (including a few whose styles are often compared to Rodman’s, some Hall of Famers, some future first-ballot Hall of Fame selections, and Rodman’s 2011 Hall of Fame co-finalists Chris Mullin and Maurice Cheeks):
I will put up a table of the entire list of 470 players—including win differentials and a number of other metrics that I will discuss throughout the rest of Part 3—along with section (c) on Friday.
Amazingly, this number may not even reflect Rodman’s true impact, because he generally played for extremely good teams, where it is not only harder to contribute, but where a given impact will have less of an effect on win percentage (for example, if your team normally wins 90% of its games, it is clearly impossible to have a win% differential above 10%). To account for this, I’ve also created “adjusted” win% differentials, which attempt to normalize a player’s percentage increase/decrease to what it would be on a .500 team.
This adjustment is done somewhat crudely, by measuring how far the player gets you toward 100% (for positive impacts) or toward 0% (for negative). E.g., if someone plays for a team that normally wins 70%, and they win 85% with him in the lineup, that is 50% of the way to 100%. Thus, as 50% of the way from 50% to 100% is 75%, that player’s adjusted differential is 25% (as opposed to their raw value of 15%).
A few notes about this method: While I prefer the adjusted numbers for this situation, they have their drawbacks. They are most accurate when dealing with consistently good or bad teams, over multiple seasons, and with bigger sample sizes. They are less accurate with smaller sample sizes, in individual seasons, and with uncertain team quality. This is because regression to the mean can become an interfering factor. When looking at individual seasons in a void, it is relatively easy to account for both effects, which I do for my league-wide win differential analysis. But when aggregating independent seasons that have a common related element—such as the same team or player—you basically have to pick your poison (of course, there may be some way to deal with this issue that I just don’t know or haven’t thought of yet). I will tend to use the adjusted numbers for this analysis, but though they are slightly more favorable to Rodman, either metric leads to the same bottom line. In any case, the tables I will be posting include both metrics (as well as other options).
Dennis Rodman’s adjusted numbers boost his win differential to 21.6%, widening the margin between him and 2nd place. I know I will be flamed if I don’t add that (just as I noted in part 2(b)) I am not claiming that Rodman was actually the best player in the last 25 years. This is a volatile statistic, and Rodman merely happening to have the best win differential among the group of 470 qualifying players does not mean he was actually the best player overall, or even that he was the best player in the group. That said, we should not dismiss the extremeness of the result either:
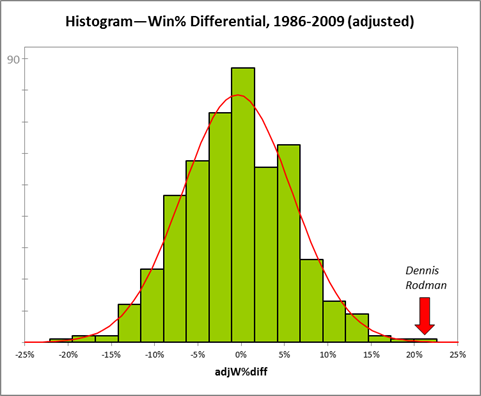
I will be using a number of (eerily similar) histograms through the rest of Part 3 as well. If you’re not familiar, histograms are one of the simplest and most useful graphical representations of single-variable data (yet, inexplicably, they aren’t built into Excel): each bar represents the number of data points of the designated value. If the variable is continuous (as it is in this case), each bar is basically a “container” that tells you how many data points fit in between the left and right values of the bar (technically it tells you the “density” of points near the center of the container, but those are effectively the same in most circumstances). Their main purpose is to eyeball how the variable is distributed—in this case, as you can see it is distributed normally.
The red line is an overlay of the normal distribution of the sample, which has a mean of –0.5% and standard deviation of 6.3%. This puts Rodman just over 3.5 standard deviations above the mean, a value that should occur about once in every 4000 instances—and he does this based on a standard deviation that is derived from a pool that includes the statistics of many players that have as little as 1/4th as much relevant data as he has.
Moreover, as I will discuss in section (b) tomorrow, his win % differential is not only extreme relative to the rest of the NBA, it is even extreme relative to himself—and this has important implications in its own right.
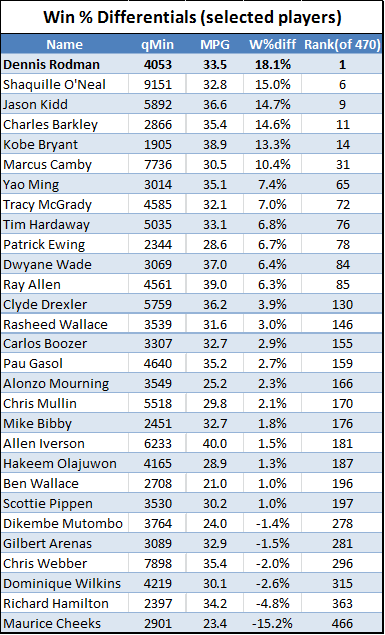
So why would a player like Dominique Wilkins, whose teams won 4.6% less of the time with him in the line up than not, hurt his team even though he was the leader of every Hawks team he played for? Does it simply go back to the perception vs value argument where he seemed to be a great player but in fact hurt his team? I am just curious as to what confidence level we can say Dominique Wilkins hurt his teams chances of winning.
It’s the eligible seasons, they are all in the nineties. This might be an inherent bias towards Rodman, because for most players, not playing is a result of injury, but for Rodman it was often suspension (tell me if I’m wrong regarding 4 of those 5 seasons). Injury might harm the team even more, as usually a player return to play at a lower level at first, and so the team is even worse when he returns, until he regains his old level of play. Suspension is different. This also might be the reason the mean is negative (although it is only marginally negative). I think there might be some bias of this sort, but only a little.
“The choice to use a designated rebounder on an offensively strong team must have been an extremely successful exploitative strategy.”
I’d like to see more research on other cases. I think the team design strategy story needs to be explored and compared to the singular athlete story.
If you can’t logically, irrefutably assign winshares among the 5 guys on the court when winning over all other winshare splits how much can any win-based evaluation say about a single player’s contribution to winning overall?
I’m not using a “Win Shares” metric, this is observed win differential.