The Case Against the Case for Dennis Rodman: Initial Volleys

When I began writing about Dennis Rodman, I was so terrified that I would miss something and the whole argument would come crashing down that I kept pushing it further and further and further, until a piece I initially planned to be about 10 pages of material ended up being more like 150. [BTW, this whole post may be a bit too inside-baseball if you haven’t actually read—or at least skimmed—my original “Case for Dennis Rodman.” If so, that link has a helpful guide.]

The downside of this, I assumed, is that the extra material should open up many angles of attack. It was a conscious trade-off, knowing that individual parts in the argument would be more vulnerable, but the Case as a whole would be thorough and redundant enough to survive any battles I might end up losing.

Ultimately, however, I’ve been a bit disappointed in the critical response. Most reactions I’ve seen have been either extremely complimentary or extremely dismissive.

So a while ago, I decided that if no one really wanted to take on the task, I would do it myself. In one of the Rodman posts, I wrote:

Give me an academic who creates an interesting and meaningful model, and then immediately devotes their best efforts to tearing it apart!

And thus The Case Against the Case for Dennis Rodman is born.

Before starting, here are a few qualifying points:

  1. I’m not a lawyer, so I have no intention of arguing things I don’t believe. I’m calling this “The Case Against the Case For Dennis Rodman,” because I cannot in good faith (barring some new evidence or argument I am as yet unfamiliar with) write The Case Against Dennis Rodman.
  2. Similarly, where I think an argument is worth being raised and discussed but ultimately fails, I will make the defense immediately (much like “Objections and Replies”).
  3. I don’t have an over-arching anti-Case hypothesis to prove, so don’t expect this series to be a systematic takedown of the entire enterprise. Rather, I will point out weaknesses as I consider them, so they may not come in any kind of predictable order.
  4. If you were paying attention, of course you noticed that The Case For Dennis Rodman was really (or at least concurrently) about demonstrating how player valuation is much more dynamic and complicated than either conventional or unconventional wisdom gives it credit for. But, for now, The Case Against the Case will focus mainly on the Dennis Rodman part.

Ok, so with this mission in mind, let me start with a bit of what’s out there already:

A Not-Completely-Stupid Forum Discussion

I admit, I spend a fair amount of time following back links to my blog. Some of that is just ego-surfing, but I’m also desperate to find worthy counter-arguments.

As I said above, that search is sometimes more fruitless than I would like. Even the more intelligent discussions usually include a lot of uninspired drivel. For example, let’s look at a recent thread on RealGM. After one person lays out a decent (though imperfect) summary of my argument, there are several responses along the lines of poster “SVictor”s:

I won’t pay attention to any study that states that [Rodman might be more valuable than Michael Jordan].

Actually, I’m pretty sympathetic to this kind of objection. There can be a bayesian ring of truth to “that is just absurd on its face” arguments (I once made a similar argument against an advanced NFL stat after it claimed Neil O’Donnell was the best QB in football). However, it’s not really a counter-argument, it’s more a meta-argument, and I think I’ve considered most of those to death. Besides, I don’t actually make the claim in question, I merely suggest it as something worth considering.

A much more detailed and interesting response comes from poster “mysticbb.” Now, he starts out pretty insultingly:

The argumentation is biased, it is pretty obvious, which makes it really sad, because I know how much effort someone has to put into such analysis.

I cannot say affirmatively that I have no biases, or that bias never affects my work. Study after study shows that this is virtually impossible. But I can say that I am completely and fundamentally committed to identifying it and stamping it out wherever I can. So, please—as I asked in my conclusion—please point out where the bias is evident and I will do everything in my power to fix it.

Oddly, though, mysticbb seems to endorse (almost verbatim) the proposition that I set out to prove:

Let me start with saying that Dennis Rodman seems to be underrated by a lot of people. He was a great player and deserved to be in the HOF, I have no doubt about that. He had great impact on the game and really improved his team while playing.

(People get so easily distracted: You write one article about a role-player maybe being better than Michael Jordan, and they forget that your overall claim is more modest.)

Of course, my analysis could just be way off, particularly in ways that favor Rodman. To that end, mysticbb raises several valid points, though with various degrees of significance.

Here he is on Rodman’s rebounding:

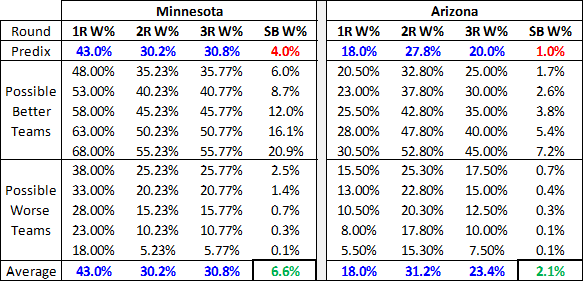
Let me start with the rebounding aspect. From 1991 to 1998 Rodman was leading the league in TRB% in each season. He had 17.7 ORB%, 33 DRB% and overall 25.4 TRB%. Those are AWESOME numbers, if we ignore context. Let us take a look at the numbers for the playoffs during the same timespan: 15.9 ORB%, 27.6 DRB% and 21.6 TRB%. Still great numbers, but obviously clearly worse than his regular season numbers. Why? Well, Rodman had the tendency to pad his rebounding stats in the regular season against weaker teams, while ignoring defensive assignments and fighting his teammates for rebounds. All that was eliminated during the playoffs and his numbers took a hit.

Now, I don’t know how much I talked about the playoffs per se, but I definitely discussed—and even argued myself—that Rodman’s rebounding numbers are likely inflated. But I also argued that if that IS the case, it probably means Rodman was even more valuable overall (see that same link for more detail). He continues:

Especially when we look at the defensive rebounding part, during the regular season he is clearly ahead of Duncan or Garnett, but in the playoffs they are all basically tied. Now imagine, Rodman brings his value via rebounding, what does that say about him, if that value is matched by players like Duncan or Garnett who both are also great defenders and obviously clearly better offensive players?

Now, as I noted at the outset Rodman’s career offensive rebounding percentage is approximately equal to Kevin Garnett’s career overall rebounding percentage, so I think Mystic is making a false equivalency based on a few cherry-picked stats.

But, for a moment, let’s assume it were true that Garnett/Duncan had similar rebounding numbers to Rodman, so what? Rodman’s crazy rebounding numbers cohere nicely with the rest of the puzzle as an explanation of why he was so valuable—his absurd rebounding stats make his absurd impact stats more plausible and vice versa—but they’re technically incidental. Indeed, they’re even incidental to his rebounding contribution: The number (or even percent) of rebounds a player gets does not correlate very strongly with the number of rebounds he has actually added to his team (nor does a player’s offensive “production” correlate very strongly with improvement in a team’s offense), and it does so the most on the extremes.

But I give the objection credit in this regard: The playoff/regular season disparity in Rodman’s rebounding numbers (though let’s not overstate the case, Rodman has 3 of the top 4 TRB%’s in playoff history) do serve to highlight how dynamic basketball statistics are. The original Case For Dennis Rodman is perhaps too willing to draw straight causal lines, and that may be worth looking into. Also, a more thorough examination of Rodman’s playoff performance may be in order as well.

On the indirect side of The Case, mysticbb has this to say:

[T]he high difference between the team performance in games with Rodman and without Rodman is also caused by a difference in terms of strength of schedule, HCA and other injured players.

I definitely agree that my crude calculation of Win % differentials does not control for a number of things that could be giving Rodman, or any other player, a boost. Controlling for some of these things is probably possible, if more difficult than you might think. This is certainly an area where I would like to implement some more robust comparison methods (and I’m slowly working on it).

But, ultimately, all of the factors mysticbb mentions are noise. Circumstances vary and lots of things happen when players miss games, and there are a lot of players and a lot of circumstances in the sample that Rodman is compared to: everyone has a chance to get lucky. That chance is reflected in my statistical significance calculations.

Mysticbb makes some assertions about Rodman having a particularly favorable schedule, but cites only the 1997 Bulls, and it’s pretty thin gruel:

If we look at the 12 games with Kukoc instead of Rodman we are getting 11.0 SRS. So, Rodman over Kukoc made about 0.5 points.

Of course, if there is evidence that Rodman was especially lucky over his career, I would like to see it. But, hmm, since I’m working on the Case Against myself, I guess that’s my responsibility as well. Fair enough, I’ll look into it.

Finally, mysticbb argues:

The last point which needs to be considered is the offcourt issues Rodman caused, which effected the outcome of games. Take the 1995 Spurs for example, when Rodman refused to guard Horry on the perimeter leading to multiple open 3pt shots for Horry including the later neck-breaker in game 6. The Spurs one year later without Rodman played as good as in 1995 with him.

I don’t really have much to say on the first part of this. As I noted at the outset, there’s some chance that Rodman caused problems on his team, but I feel completely incompetent to judge that sort of thing. But the other part is interesting: It’s true that the Spurs were only 5% worse in 95-96 than they were in 94-95 (OFC, they would be worse measuring only against games Rodman played in), but cross-season comparisons are obviously tricky, for a number of reasons. And if they did exist, I’m not sure they would break the way suggested. For example, the 2nd Bulls 3-peat teams were about as much better than the first Bulls 3-peat as the first Bulls 3-peat was better than the 93-95 teams that were sans Michael Jordan.

That said, I actually do find multi-season comparisons to be a valid area for exploration. So, e.g., I’ve spent some time looking at rookie impact and how predictive it is of future success (answer: probably more than you think).

Finally, a poster named “parapooper” makes some points that he credits to me, including:

He also admits that Rodman actually has a big advantage in this calculation because he missed probably more games than any other player due to reasons other than health and age.

I don’t actually remember making this point, at least this explicitly, but it is a valid concern IMO. A lot of the In/Out numbers my system generated include seasons where players were old or infirm, which disadvantages them. In fact, I initially tried to excise these seasons, and tried accounting for them in a variety of ways, such as comparing “best periods” to “best periods”, etc. But I found such attempts to be pretty unwieldy and arbitrary, and they shrunk the sample size more than I thought they were worth, without affecting the bottom line: Rodman just comes out on top of a smaller pile. That said, some advantage to Rodman relative to others must exist, and quantifying that advantage is a worthy goal.

A similar problem that “para” didn’t mention specifically is that a number of the in/out periods for players include spots where the player was traded. In subsequent analysis, I’ve confirmed what common sense would probably indicate: A player’s differential stats in trade scenarios are much less reliable. Future versions of the differential comparison should account for this, one way or another.

The differential analysis in the series does seem to be the area that most needs upgrading, though the constant trade-off between more information and higher quality information means it will never be as conclusive as we might want it to be. Not mentioned in this thread (that I saw), but what I will certainly deal with myself, are broader objections to the differential comparisons as an enterprise. So, you know. Stay tuned.

Sports Geek Mecca: Recap and Thoughts, Part 1

So, over the weekend, I attended my second MIT Sloan Sports Analytics Conference. My experience was much different than in 2011: Last year, I went into this thing barely knowing that other people were into the same things I was. An anecdote: In late 2010, I was telling my dad how I was about to have a 6th or 7th round interview for a pretty sweet job in sports analysis, when he speculated, “How many people can there even be in that business? 10? 20?” A couple of months later, of course, I would learn.

A lot has happened in my life since then: I finished my Rodman series, won the ESPN Stat Geek Smackdown (which, though I am obviously happy to have won, is not really that big a deal—all told, the scope of the competition is about the same as picking a week’s worth of NFL games), my wife and I had a baby, and, oh yeah, I learned a ton about the breadth, depth, and nature of the sports analytics community.

For the most part, I used Twitter as sort of my de facto notebook for the conference.  Thus, I’m sorry if I’m missing a bunch of lengthier quotes and/or if I repeat a bunch of things you already saw in my live coverage, but I will try to explain a few things in a bit more detail.

For the most part, I’ll keep the recap chronological.  I’ve split this into two parts: Part 1 covers Friday, up to but not including the Bill Simmons/Bill James interview.  Part 2 covers that interview and all of Saturday.

Opening Remarks:

From the pregame tweets, John Hollinger observed that 28 NBA teams sent representatives (that we know of) this year.  I also noticed that the New England Revolution sent 2 people, while the New England Patriots sent none, so I’m not sure that number of official representatives reliably indicates much.

The conference started with some bland opening remarks by Dean David Schmittlein.  Tangent: I feel like political-speak (thank everybody and say nothing) seems to get more and more widespread every year. I blame it on fear of the internet. E.g., in this intro segment, somebody made yet another boring joke about how there were no women present (personally, I thought there were significantly more than last year), and was followed shortly thereafter by a female speaker, understandably creating a tiny bit of awkwardness. If that person had been more important (like, if I could remember his name to slam him), I doubt he would have made that joke, or any other joke. He would have just thanked everyone and said nothing.

The Evolution of Sports Leagues

Featuring Gary Bettman (NHL), Rob Manfred (MLB), Adam Silver (NBA), Steve Tisch (NYG) and Michael Wilbon moderating.

This panel really didn’t have much of a theme, it was mostly Wilbon creatively folding a bunch of predictable questions into arbitrary league issues.  E.g.: ” “What do you think about Jeremy Lin?!? And, you know, overseas expansion blah blah.”

I don’t get the massive cultural significance of Jeremy Lin, personally.  I mean, he’s not the first ethnically Chinese player to have NBA success (though he is perhaps the first short one).  The discussion of China, however, was interesting for other reasons. Adam Silver claimed that Basketball is already more popular in China than soccer, with over 300 million Chinese people playing it.  Those numbers, if true, are pretty mind-boggling.

Finally, there was a whole part about labor negotiations that was pretty well summed up by this tweet:

Hockey Analytics

Featuring Brian Burke, Peter Chiarelli, Mike Milbury and others.

The panel started with Peter Chiarelli being asked how the world champion Boston Bruins use analytics, and in an ominous sign, he rambled on for a while about how, when it comes to scouting, they’ve learned that weight is probably more important than height.

Overall, it was a bit like any scene from the Moneyball war room, with Michael Schuckers (the only pro-stats guy) playing the part of Jonah Hill, but without Brad Pitt to protect him.

When I think of Brian Burke, I usually think of Advanced NFL Stats, but apparently there’s one in Hockey as well.  Burke is GM/President of the Toronto Maple Leafs. At one point he was railing about how teams that use analytics have never won anything, which confused me since I haven’t seen Toronto hoisting any Stanley Cups recently, but apparently he did win a championship with the Mighty Ducks in 2007, so he clearly speaks with absolute authority.

This guy was a walking talking quote machine for the old school. I didn’t take note of all the hilarious and/or non-sensical things he said, but for some examples, try searching Twitter for “#SSAC Brian Burke.” To give an extent of how extreme, someone tweeted this quote at me, and I have no idea if he actually said it or if this guy was kidding.

In other words, Burke was literally too over the top to effectively parody.

On the other hand, in the discussion of concussions, I thought Burke had sort of a folksy realism that seemed pretty accurate to me.  I think his general point is right, if a bit insensitive: If we really changed hockey so much as to eliminate concussions entirely, it would be a whole different sport (which he also claimed no one would watch, an assertion which is more debatable imo).  At the end of the day, I think professional sports mess people up, including in the head.  But, of course, we can’t ignore the problem, so we have to keep proceeding toward some nebulous goal.

Mike Milbury, presently a card-carrying member of the media, seemed to mostly embrace the alarmist media narrative, though he did raise at least one decent point about how the increase in concussions—which most people are attributing to an increase in diagnoses—may relate to recent rules changes that have sped up the game.

But for all that, the part that frustrated me the most was when Michael Schuckers, the legitimate hockey statistician at the table, was finally given the opportunity to talk.  90% of the things that came out of his mouth were various snarky ways of asserting that face-offs don’t matter.  I mean, I assume he’s 100% right, but just had no clue how to talk to these guys.  Find common ground: you both care about scoring goals, defending goals, and winning.  Good face-off skill get you the puck more often in the right situations. The question is how many extra possessions you get and how valuable those possessions are? And finally, what’s the actual decision in question?

Baseball Analytics

Featuring Scott Boras, Scott Boras, Scott Boras, some other guys, Scott Boras, and, oh yeah, Bill James.

In stark constrast to the Hockey panel, the Baseball guys pretty much bent over backwards to embrace analytics as much as possible.  As I tweeted at the time:

Scott Boras seems to like hearing Scott Boras talk.  Which is not so bad, because Scott Boras actually did seem pretty smart and well informed: Among other things, Scott Boras apparently has a secret internal analytics team. To what end, I’m not entirely sure, since Scott Boras also seemed to say that most GM’s overvalue players relative to what Scott Boras’s people tell Scott Boras.

At this point, my mind wandered:

How awesome would that be, right?

Anyway, in between Scott Boras’s insights, someone asked this Bill James guy about his vision for the future of baseball analytics, and he gave two answers:

  1. Evaluating players from a variety of contexts other than the minor leagues (like college ball, overseas, Cubans, etc).
  2. Analytics will expand to look at the needs of the entire enterprise, not just individual players or teams.

Meh, I’m a bit underwhelmed.  He talked a bit about #1 in his one-on-one with Bill Simmons, so I’ll look at that a bit more in my review of that discussion. As for #2, I think he’s just way way off: The business side of sports is already doing tons of sophisticated analytics—almost certainly way more than the competition side—because, you know, it’s business.

E.g., in the first panel, there was a fair amount of discussion of how the NBA used “sophisticated modeling” for many different lockout-related analyses (I didn’t catch the Ticketing Analytics panel, but from its reputation, and from related discussions on other panels, it sounds like that discipline has some of the nerdiest analysis of all).

Scott Boras let Bill James talk about a few other things as well:  E.g., James is not a fan of new draft regulations, analogizing them to government regulations that “any economist would agree” inevitably lead to market distortions and bursting bubbles.  While I can’t say I entirely disagree, I’m going to go out on a limb and guess that his political leanings are probably a bit Libertarian?

Basketball Analytics

Featuring Jeff Van Gundy, Mike Zarren, John Hollinger, and Mark Cuban Dean Oliver.

If every one of these panels was Mark Cuban + foil, it would be just about the most awesome weekend ever (though you might not learn the most about analytics). So I was excited about this one, which, unfortunately, Cuban missed. Filling in on zero/short notice was Dean Oliver.  Overall, here’s Nathan Walker’s take:

This panel actually had some pretty interesting discussions, but they flew by pretty fast and often followed predictable patterns, something like this:

  1. Hollinger says something pro-stats, though likely way out of his depth.
  2. Zarren brags about how they’re already doing that and more on the Celtics.
  3. Oliver says something smart and nuanced that attempts to get at the underlying issues and difficulties.
  4. Jeff Van Gundy uses forceful pronouncements and “common sense” to dismiss his strawman version of what the others have been saying.

E.g.:

Zarren talked about how there is practically more data these days than they know what to do with.  This seems true and I think it has interesting implications. I’ll discuss it a little more in Part 2 re: the “Rebooting the Box Score” talk.

There was also an interesting discussion of trades, and whether they’re more a result of information asymmetry (in other words, teams trying to fleece each other), or more a result of efficient trade opportunities (in other words, teams trying to help each other).  Though it really shouldn’t matter—you trade when you think it will help you, whether it helps your trade partner is mostly irrelevant—Oliver endorsed the latter.  He makes the point that, with such a broad universe of trade possibilities, looking for mutually beneficial situations is the easiest way to find actionable deals.  Fair enough.

Coaching Analytics

Featuring coaching superstars Jeff Van Gundy, Eric Mangini, and Bill Simmons.  Moderated by Daryl Morey.

OK, can I make the obvious point that Simmons and Morey apparently accidentally switched role cards?  As a result, this talk featured a lot of Simmons attacking coaches and Van Gundy defending them.  I honestly didn’t remember Mangini was on this panel until looking back at the book (which is saying something, b/c Mangini usually makes my blood boil).

There was almost nothing on, say, how to evaluate coaches, say, by analyzing how well their various decisions comported with the tenets of win maximization.  There was a lengthy (and almost entirely non-analytical) discussion of that all-important question of whether an NBA coach should foul or not up by 3 with little time left.  Fouling probably has a tiny edge, but I think it’s too close and too infrequent to be very interesting (though obviously not as rare, it reminds me a bit of the impassioned debates you used to see on Poker forums about whether you should fast-play or slow-play flopped quads in limit hold’em).

There was what I thought was a funny moment when Bill Simmons was complaining about how teams seem to recycle mediocre older coaches rather than try out young, fresh talent. But when challenged by Van Gundy, Simmons drew a blank and couldn’t think of anyone.  So, Bill, this is for you.  Here’s a table of NBA coaches who have coached at least 1000 games for at least 3 different teams, while winning fewer than 60% of their games and without winning any championships:

[table “8” not found /]

Note that I’m not necessarily agreeing with Simmons: Winning championships in the NBA is hard, especially if your team lacks uber-stars (you know, Michael Jordan, Magic Johnson, Dennis Rodman, et al).

Part 2 coming soon!

Honestly, I got a little carried away with my detailed analysis/screed on Bill James, and I may have to do a little revising. So due to some other pressing writing commitments, you can probably expect Part 2 to come out this Saturday (Friday at the earliest).

MIT Sloan Sports Analytics Conference, Day 1: Recap and Thoughts

This was my first time attending this conference, and Day 1 was an amazing experience.  At this point last year, I literally didn’t know that there was a term (“sports analytics”) for the stuff I liked to do in my spare time.  Now I learn that there is not only an entire industry built up around the practice, but a whole army of nerds in its society.  Naturally, I have tons of criticisms of various things that I saw and heard—that’s what I do—but I loved it, even the parts I hated.

Here are the panels and presentations that I attended, along with some of my thoughts:

Birth to Stardom: Developing the Modern Athlete in 10,000 Hours?

Featuring Malcolm Gladwell (Author of Outliers), Jeff Van Gundy (ESPN), and others I didn’t recognize.

In this talk, Gladwell rehashed his absurdly popular maxim about how it takes 10,000 hours to master anything, and then made a bunch of absurd claims about talent. (Players with talent are at a disadvantage!  Nobody wants to hire Supreme Court clerks!  Etc.) The most re-tweeted item to come out of Day 1 by far was his highly speculative assertion that “a lot of what we call talent is the desire to practice.”

While this makes for a great motivational poster, IMO his argument in this area is tautological at best, and highly deceptive at worst.  Some people have the gift of extreme talent, and some people have the gift of incredible work ethic. The streets of the earth are littered with the corpses of people who had one and not the other.  Unsurprisingly, the most successful people tend to have both.  To illustrate, here’s a random sample of 10,000 “people” with independent normally distributed work ethic and talent (each with a mean of 0, standard deviation of 1):

image

The blue dots (left axis) are simply Hard Work plotted against Talent.  The red dots (right axis) are Hard Work plotted against the sum of Hard Work and Talent—call it “total awesome factor” or “success” or whatever.  Now let’s try a little Bayes’ Theorem intuition check:  You randomly select a person and they have an awesome factor of +5.  What are the odds that they have a work ethic of better than 2 standard deviations above the mean?  High?  Does this prove that all of the successful people are just hard workers in disguise?

Hint: No.  And this illustration is conservative:  This sample is only 10,000 strong: increase to 10 billion, and the biggest outliers will be even more uniformly even harder workers (and they will all be extremely talented as well).  Moreover, this “model” for greatness is just a sum of the two variables, when in reality it is probably closer to a product, which would lead to even greater disparities.  E.g.: I imagine total greatness achieved might be something like great stuff produced per minute worked (a function of talent) times total minutes worked (a function of willpower, determination, fortitude, blah blah, etc).

The general problem with Gladwell I think is that his emphatic de-emphasis of talent (which has no evidence backing it up) cheapens his much stronger underlying observation that for any individual to fully maximize their potential takes the accumulation of a massive amount of hard work—and this is true for people regardless of what their full potential may be.  Of course, this could just be a shrewd marketing ploy on his part: you probably sell more books by selling the hope of greatness rather than the hope of being an upper-level mid-manager (especially since you don’t have to worry about that hope going unfulfilled for at least 10 years).

Read the rest of this entry »

UPDATE: Advanced NFL Stats Admits I Was Right. Sort Of.

Background:  In January, long before I started blogging in earnest, I made several comments on this Advanced NFL Stats post that were critical of Brian Burke’s playoff prediction model, particularly that, with 8 teams left, it predicted that the Dallas Cowboys had about the same chance of winning the Super Bowl as the Jets, Ravens, Vikings, and Cardinals combined. This seemed both implausible on its face and extremely contrary to contract prices, so I was skeptical.  In that thread, Burke claimed that his model was “almost perfectly calibrated. Teams given a 0.60 probability to win do win 60% of the time, teams given a 0.70 probability win 70%, etc.”  I expressed interest in seeing his calibration data, ”especially for games with considerable favorites, where I think your model overstates the chances of the better team,” but did not get a response.

I brought this dispute up in my monstrously-long passion-post, “Applied Epistemology in Politics and the Playoffs,” where I explained how, even if his model was perfectly calibrated, it would still almost certainly be underestimating the chances of the underdogs.  But now I see that Burke has finally posted the calibration data (compiled by a reader from 2007 on).  It’s a very simple graph, which I’ve recreated here, with a trend-line for his actual data:

image

Now I know this is only 3+ years of data, but I think I can spot a trend:  for games with considerable favorites, his model seems to overstate the chances of the better team.  Naturally, Burke immediately acknowledges this error:

On the other hand, there appears to be some trends. the home team is over-favored in mismatches where it is the stronger team and is under-favored in mismatches where it is the weaker team. It’s possible that home field advantage may be even stronger in mismatches than the model estimates.

Wait, what? If the error were strictly based on stronger-than-expected home-field advantage, the red line should be above the blue line, as the home team should win more often than the model projects whether it is a favorite or not – in other words, the actual trend-line would be parallel to the “perfect” line but with a higher intercept.  Rather, what we see is a trend-line with what appears to be a slightly higher intercept but a somewhat smaller slope, creating an “X” shape, consistent with the model being least accurate for extreme values.  In fact, if you shifted the blue line slightly upward to “shock” for Burke’s hypothesized home-field bias, the “X” shape would be even more perfect: the actual and predicted lines would cross even closer to .50, while diverging symmetrically toward the extremes.

Considering that this error compounds exponentially in a series of playoff games, this data (combined with the still-applicable issue I discussed previously), strongly vindicates my intuition that the market is more trustworthy than Burke’s playoff prediction model, at least when applied to big favorites and big dogs.

Yes ESPN, Professional Kickers are Big Fat Chokers

A couple of days ago, ESPN’s Peter Keating blogged about “icing the kicker” (i.e., calling timeouts before important kicks, sometimes mere instants before the ball is snapped).  He argues that the practice appears to work, at least in overtime.  Ultimately, however, he concludes that his sample is too small to be “statistically significant.”  This may be one of the few times in history where I actually think a sports analyst underestimates the probative value of a small sample: as I will show, kickers are generally worse in overtime than they are in regulation, and practically all of the difference can be attributed to iced kickers.  More importantly, even with the minuscule sample Keating uses, their performance is so bad that it actually is “significant” beyond the 95% level.

In Keating’s 10 year data-set, kickers in overtime only made 58.1% of their 35+ yard kicks following an opponent’s timeout, as opposed to 72.7% when no timeout was called.  The total sample size is only 75 kicks, 31 of which were iced.  But the key to the analysis is buried in the spreadsheet Keating links to: the average length of attempted field goals by iced kickers in OT was only 41.87 yards, vs. 43.84 yards for kickers at room temperature.  Keating mentions this fact in passing, mainly to address the potential objection that perhaps the iced kickers just had harder kicks — but the difference is actually much more significant.
To evaluate this question properly, we first need to look at made field goal percentages broken down by yard-line.  I assume many people have done this before, but in 2 minutes of googling I couldn’t find anything useful, so I used play-by-play data from 2000-2009 to create the following graph:

image

The blue dots indicate the overall field-goal percentage from each yard-line for every field goal attempt in the period (around 7500 attempts total – though I’ve excluded the one 76 yard attempt, for purely aesthetic reasons).  The red dots are the predicted values of a logistic regression (basically a statistical tool for predicting things that come in percentages) on the entire sample.  Note this is NOT a simple trend-line — it takes every data point into account, not just the averages.  If you’re curious, the corresponding equation (for predicted field goal percentage based on yard line x) is as follows:

 \large{1 - \dfrac{e^{-5.5938+0.1066x}} {1+e^{-5.5938+0.1066x}}}

The first thing you might notice about the graph is that the predictions appear to be somewhat (perhaps unrealistically) optimistic about very long kicks.  There are a number of possible explanations for this, chiefly that there are comparatively few really long kicks in the sample, and beyond a certain distance the angle of the kick relative to the offensive and defensive linemen becomes a big factor that is not adequately reflected by the rest of the data (fortunately, this is not important for where we are headed).  The next step is to look at a similar graph for overtime only — since the sample is so much smaller, this time I’ll use a bubble-chart to give a better idea of how many attempts there were at each distance:

image

For this graph, the sample is about 1/100th the size of the one above, and the regression line is generated from the OT data only.  As a matter of basic spatial reasoning — even if you’re not a math whiz — you may sense that this line is less trustworthy.  Nevertheless, let’s look at a comparison of the overall and OT-based predictions for the 35+ yard attempts only:

image

Note: These two lines are slightly different from their counterparts above.  To avoid bias created by smaller or larger values, and to match Keating’s sample, I re-ran the regressions using only 35+ yard distances that had been attempted in overtime (they turned out virtually the same anyway).

Comparing the two models, we can create a predicted “Choke Factor,” which is the percentage of the original conversion rate that you should knock off for a kicker in an overtime situation:

image

A weighted average (by the number of OT attempts at each distance) gives us a typical Choke Factor of just over 6%.  But take this graph with a grain of salt: the fact that it slopes upward so steeply is a result of the differing coefficients in the respective regression equations, and could certainly be a statistical artifact.  For my purposes however, this entire digression into overtime performance drop-offs is merely for illustration:  The main calculation relevant to Keating’s iced kick discussion is a simple binomial probability:  Given an average kick length of 41.87 yards, which carries a predicted conversion rate of 75.6%, what are the odds of converting only 18 or fewer out of 31 attempts?  OK, this may be a mildly tricky problem if you’re doing it longhand, but fortunately for us, Excel has a BINOM.DIST() function that makes it easy:

image

Note : for people who might not pick:  Yes, the predicted conversion rate for the average length is not going to be exactly the same as the average predicted value for the length of each kick.  But it is very close, and close enough.

As you can see, the OT kickers who were not iced actually did very slightly better than average, which means that all of the negative bias observed in OT kicking stems from the poor performance seen in just 31 iced kick attempts.  The probability of this result occurring by chance — assuming the expected conversion rate for OT iced kicks were equal to the expected conversion rate for kicks overall — would be only 2.4%.  Of course, “probability of occurring by chance” is the definition of statistical significance, and since 95% against (i.e., less than 5% chance of happening) is the typical threshold for people to make bold assertions, I think Keating’s statement that this “doesn’t reach the level of improbability we need to call it statistically significant” is unnecessarily humble.  Moreover, when I stated that the key to this analysis was the 2 yard difference that Keating glossed over, that wasn’t for rhetorical flourish:  if the length of the average OT iced kick had been the same as the length of the average OT regular kick,  the 58.1% would correspond to a “by chance” probability of 7.6%, obviously not making it under the magic number.

A History of Hall of Fame QB-Coach Entanglement

Last week on PTI, Dan LeBatard mentioned an interesting stat that I had never heard before: that 13 of 14 Hall of Fame coaches had Hall of Fame QB’s play for them.  LeBatard’s point was that he thought great quarterbacks make their coaches look like geniuses, and he was none-too-subtle about the implication that coaches get too much credit.  My first thought was, of course: Entanglement, anyone? That is to say, why should he conclude that the QB’s are making their coaches look better than they are instead of the other way around?  Good QB’s help their teams win, for sure, but winning teams also make their QB’s look good.  Thus – at best – LeBatard’s stat doesn’t really imply that HoF Coaches piggyback off of their QB’s success, it implies that the Coach and QB’s successes are highly entangled.  By itself, this analysis might be enough material for a tweet, but when I went to look up these 13/14 HoF coach/QB pairs, I found the history to be a little more interesting than I expected.

First, I’m still not sure exactly which 14 HoF coaches LeBatard was talking about.  According the the official website, there are 21 people in the HoF as coaches.  From what I can tell, 6 of these (Curly Lambeau, Ray Flaherty, Earle Neale, Jimmy Conzelman, Guy Chamberlain and Steve Owen) coached before the passing era, so that leaves 15 to work with.  A good deal of George Halas’s coaching career was pre-pass as well, but he didn’t quit until 1967 – 5 years later than Paul Brown – and he coached a Hall of Fame QB anyway (Sid Luckman).  Of the 15, 14 did indeed coach HoF QB’s, at least technically.

To break the list down a little, I applied two threshold tests:  1) Did the coach win any Super Bowls (or league championships before the SB era) without their HoF QB?  And 2) In the course of his career, did the coach have more than one HoF QB?  A ‘yes’ answer to either of these questions I think precludes the stereotype of a coach piggybacking off his star player (of course, having coached 2 or more Hall of Famer’s might just mean that coach got extra lucky, but subjectively I think the proxy is fairly accurate).  Here is the list of coaches eliminated by these questions:

[table “5” not found /]
Joe Gibbs wins the outlier prize by a mile: not only did he win 3 championships “on his own,” he did it with 3 different non-HoF QB’s.  Don Shula had 3 separate eras of greatness, and I think would have been a lock for the hall even with the Griese era excluded.  George Allen never won a championship, but he never really had a HoF QB either: Jurgensen (HoF) served as Billy Kilmer (non-HoF)’s backup for the 4 years he played under Allen.  Sid Gillman had a long career, his sole AFL championship coming with the Chargers in 1963 – with Tobin Rote (non-HoF) under center.  Weeb Ewbank won 2 NFL championships in Baltimore with Johnny Unitas, and of course won the Super Bowl against Baltimore and Unitas with Joe Namath.  Finally, George Halas won championships with Pard Pearce (5’5”, non-HoF), Carl Brumbaugh (career passer rating: 34.9, non-HoF), Sid Luckman (HoF) and Billy Wade (non-HoF).  Plus, you know, he’s George Halas.
[table “1” not found /]
Though Chuck Noll won all of his championships with Terry Bradshaw (HoF), those Steel Curtain teams weren’t exactly carried by the QB position (e.g., in the 1974 championship season, Bradshaw averaged less than 100 passing yards per game).  Bill Walsh is a bit more borderline: not only did all of his championships come with Joe Montana, but Montana also won a Super Bowl without him.  However, considering Walsh’s reputation as an innovator, and especially considering his incredible coaching tree (which has won nearly half of all the Super Bowls since Walsh retired in 1989), I’m willing to give him credit for his own notoriety.  Finally, Vince Lombardi, well, you know, he’s Vince Lombardi.

Which brings us to the list of the truly entangled:
[table “4” not found /]
I waffled a little on Paul Brown, as he is generally considered an architect of the modern league (and, you know, a team is named after him), but unlike Lombardi, Walsh and Knoll, Brown’s non-Otto-Graham-entangled accomplishments are mostly unrelated to coaching.  I’m sure various arguments could be made about individual names (like, “You crazy, Tom Landry is awesome”), but the point of this list isn’t to denigrate these individuals, it’s simply to say that these are the HoF coaches whose coaching successes are the most difficult to isolate from their quarterback’s.

I don’t really want to speculate about any broader implications, both because the sample is too small to make generalizations, and because my intuition is that coaches probably do get too much credit for their good fortune (whether QB-related or not).  But regardless, I think it’s clear that LeBatard’s 13/14 number is highly misleading.

Applied Epistemology in Politics and the Playoffs

Two nights ago, as I was watching cable news and reading various online articles and blog posts about Christine O’Donnell’s upset win over Michael Castle in Delaware’s Republican Senate primary, the hasty, almost ferocious emergence of consensus among the punditocracy – to wit, that the GOP now has virtually zero chance of picking up that seat in November – reminded me of an issue that I’ve wanted to blog about since long before I began blogging in earnest: NFL playoff prediction models.

Specifically, I have been critical of those models that project the likelihood of each surviving team winning the Super Bowl by applying a logistic regression model (i.e., “odds of winning based on past performance”) to each remaining game.  In January, I posted a number of comments to this article on Advanced NFL Stats, in which I found it absurd that, with 8 teams left, his model predicted that the Dallas Cowboys had about the same chance of winning the Super Bowl as the Jets, Ravens, Vikings, and Cardinals combined. In the brief discussion, I gave two reasons (in addition to my intuition): first, that these predictions were wildly out of whack with contract prices in sports-betting markets, and second, that I didn’t believe the model sufficiently accounted for “variance in the underlying statistics.”  Burke suggested that the first point is explained by a massive epidemic of conjunction-fallacyitis among sports bettors.  On its face, I think this is a ridiculous explanation: i.e., does he really believe that the market-movers in sports betting — people who put up hundreds of thousands (if not millions) of dollars of their own money — have never considered multiplying the odds of several games together?  Regardless, in this post I will put forth a much better explanation for this disparity than either of us proffered at the time, hopefully mooting that discussion.  On my second point, he was more dismissive, though I was being rather opaque (and somehow misspelled “beat” in one reply), so I don’t blame him.  However, I do think Burke’s intellectual hubris regarding his model (aka “model hubris”) is notable – not because I have any reason to think Burke is a particularly hubristic individual, but because I think it is indicative of a massive epidemic of model-hubrisitis among sports bloggers.

In Section 1 of this post, I will discuss what I personally mean by “applied epistemology” (with apologies to any actual applied epistemologists out there) and what I think some of its more-important implications are.  In Section 2, I will try to apply these concepts by taking a more detailed look at my problems with the above-mentioned playoff prediction models.

Section 1: Applied Epistemology Explained, Sort Of

For those who might not know, “epistemology” is essentially a fancy word for the “philosophical study of knowledge,” which mostly involves philosophers trying to define the word “knowledge” and/or trying to figure out what we know (if anything), and/or how we came to know it (if we do).  For important background, read my Complete History of Epistemology (abridged), which can be found here: In Plato’s Theaetetus, Socrates suggests that knowledge is something like “justified true belief.”  Agreement ensues.  In 1963, Edmund Gettier suggests that a person could be justified in believing something, but it could be true for the wrong reasons.  Debate ensues.  The End.

A “hot” topic in the field recently has been dealing with the implications of elaborate thought experiments similar to the following:

*begin experiment*
Imagine yourself in the following scenario:  From childhood, you have one burning desire: to know the answer to Question X.  This desire is so powerful that you dedicate your entire life to its pursuit.  You work hard in school, where you excel greatly, and you master every relevant academic discipline, becoming a tenured professor at some random elite University, earning multiple doctorates in the process.  You relentlessly refine and hone your (obviously considerable) reasoning skills using every method you can think of, and you gather and analyze every single piece of empirical data relevant to Question X available to man.  Finally, after decades of exhaustive research and study, you have a rapid series of breakthroughs that lead you to conclude – not arbitrarily, but completely based on the proof you developed through incredible amounts of hard work and ingenuity — that the answer to Question X is definitely, 100%, without a doubt: 42.  Congratulations!  To celebrate the conclusion of this momentous undertaking, you decide to finally get out of the lab/house/library and go celebrate, so you head to a popular off-campus bar.  You are so overjoyed about your accomplishment that you decide to buy everyone a round of drinks, only to find that some random guy — let’s call him Neb – just bought everyone a round of drinks himself.  What a joyous occasion: two middle-aged individuals out on the town, with reason to celebrate (and you can probably see where this is going, but I’ll go there anyway)!  As you quickly learn, it turns out that Neb is around your same age, and is also a professor at a similarly elite University in the region.  In fact, it’s amazing how much you two have in common:  you have relatively similar demographic histories, identical IQ, SAT, and GRE scores, you both won multiple academic awards at every level, you have both achieved similar levels of prominence in your academic community, and you have both been repeatedly published in journals of comparable prestige.  In fact, as it turns out, you have both been spent your entire lives studying the same question!  You have both read all the same books, you have both met, talked or worked with many comparably intelligent — or even identical — people:  It is amazing that you have never met!  Neb, of course, is feeling so celebratory because finally, after decades of exhaustive research and study, he has just had a rapid series of breakthroughs that lead him to finally conclude – not arbitrarily, but completely based on the proof he developed through incredible amounts of hard work and ingenuity — that the answer to Question X is definitely, 100%, without a doubt: 54.

You spend the next several hours drinking and arguing about Question X: while Neb seemed intelligent enough at first, everything he says about X seems completely off base, and even though you make several excellent points, he never seems to understand them.  He argues from the wrong premises in some areas, and draws the wrong conclusions in others.  He massively overvalues many factors that you are certain are not very important, and is dismissive of many factors that you are certain are crucial.  His arguments, though often similar in structure to your own, are extremely unpersuasive and don’t seem to make any sense, and though you try to explain yourself to him, he stubbornly refuses to comprehend your superior reasoning.  The next day, you stumble into class, where your students — who had been buzzing about your breakthrough all morning — begin pestering you with questions about Question X and 42.  In your last class, you had estimated that the chances of 42 being “the answer” were around 90%, and obviously they want to know if you have finally proved 42 for certain, and if not, how likely you believe it is now.  What do you tell them?

All of the research and analysis you conducted since your previous class had, indeed, led you to believe that 42 is a mortal lock.  In the course of your research, everything you have thought about or observed or uncovered, as well as all of the empirical evidence you have examined or thought experiments you have considered, all lead you to believe that 42 is the answer.  As you hesitate, your students wonder why, even going so far as to ask, “Have you heard any remotely persuasive arguments against 42 that we should be considering?”  Can you, in good conscience, say that you know the answer to Question X?  For that matter, can you even say that the odds of 42 are significantly greater than 50%?  You may be inclined, as many have been, to “damn the torpedoes” and act as if Neb’s existence is irrelevant.  But that view is quickly rebutted:  Say one of your most enterprising students brings a special device to class:  when she presses the red button marked “detonate,” if the answer to Question X is actually 42, the machine will immediately dispense $20 bills for everyone in the room; but if the answer is not actually 42, it will turn your city into rubble.  And then it will search the rubble, gather any surviving puppies or kittens, and blend them.

So assuming you’re on board that your chance encounter with Professor Neb implies that, um, you might be wrong about 42, what comes next?  There’s a whole interesting line of inquiry about what the new likelihood of 42 is and whether anything higher than 50% is supportable, but that’s not especially relevant to this discussion.  But how about this:  Say the scenario proceeds as above, you dedicate your life, yadda yadda, come to be 100% convinced of 42, but instead of going out to a bar, you decide to relax with a bubble bath and a glass of Pinot, while Neb drinks alone.  You walk into class the next day, and proudly announce that the new odds of 42 are 100%.  Mary Kate pulls out her special money-dispensing device, and you say sure, it’s a lock, press the button.  Yay, it’s raining Andrew Jacksons in your classroom!  And then: **Boom** **Meow** **Woof** **Whirrrrrrrrrrrrrr**.  Apparently Mary Kate had a twin sister — she was in Neb’s class.

*end experiment*

In reality, the fact that you might be wrong, even when you’re so sure you’re right, is more than a philosophical curiosity, it is a mathematical certainty.  The processes that lead you to form beliefs, even extremely strong ones, are imperfect.  And when you are 100% certain that a belief-generating process is reliable, the process that led you to that belief is likely imperfect.  This line of thinking is sometimes referred to as skepticism — which would be fine if it weren’t usually meant as a pejorative.

When push comes to shove, people will usually admit that there is at least some chance they are wrong, yet they massively underestimate just what those chances are.  In political debates, for example, people may admit that there is some miniscule possibility that their position is ill-informed or empirically unsound, but they will almost never say that they are more likely to be wrong than to be right.  Yet, when two populations hold diametrically opposed views, either one population is wrong or both are – all else being equal, the correct assessment in such scenarios is that no-one is likely to have it right.

When dealing with beliefs about probabilities, the complications get even trickier:  Obviously many people believe some things are close to 100% likely to be true, when the real probability may be some-much if not much-much lower.  But in addition to the extremes, people hold a whole range of poorly-calibrated probabilistic beliefs, like believing something is 60% likely when it is actually 50% or 70%.  (Note: Some Philosophically trained readers may balk at this idea, suggesting that determinism entails everything having either a 0 or 100% probability of being true.  While this argument may be sound in classroom discussions, it is highly unpragmatic: If I believe that I will win a coin flip 60% of the time, it may be theoretically true that the universe has already determined whether the coin will turn up heads or tails, but for all intents and purposes, I am only wrong by 10%).

But knowing that we are wrong so much of the time doesn’t tell us much by itself: it’s very hard to be right, and we do the best we can.  We develop heuristics that tend towards the right answers, or — more importantly for my purposes — that allow the consequences of being wrong in both directions even out over time.  You may reasonably believe that the probability of something is 30%, when, in reality, the probability is either 20% or 40%.  If the two possibilities are equally likely, then your 30% belief may be functionally equivalent under many circumstances, but they are not the same, as I will demonstrate in Section 2 (note to the philosophers: you may have noticed that this is a bit like the Gettier examples: you might be “right,” but for the wrong reasons).

There is a science to being wrong, and it doesn’t mean you have to mope in your study, or act in bad faith when you’re out of it.  “Applied Epistemology” (at least as this armchair philosopher defines it) is the study of the processes that lead to knowledge and beliefs, and of the practical implications of their limitations.

Part 2:  NFL Playoff Prediction Models

Now, let’s finally return to the Advanced NFL Stats playoff prediction model.  Burke’s methodology is simple: using a logistic regression based on various statistical indicators, the model estimates a probability for each team to win their first round matchup.  It then repeats the process for all possible second round matchups, weighting each by its likelihood of occurring (as determined by the first round projections) and so on through the championship.  With those results in hand, a team’s chances of winning the tournament is simply the product of their chances of winning in each round.  With 8 teams remaining in the divisional stage, the model’s predictions looked like this:

image

Burke states that the individual game prediction model has a “history of accuracy” and is well “calibrated,” meaning that, historically, of the teams it has predicted to win 30% of the time, close to 30% of them have won, and so on.  For a number of reasons, I remain somewhat skeptical of this claim, especially when it comes to “extreme value” games where the model predicts very heavy favorites or underdogs.  (E.g’s:  What validation safeguards do they deploy to avoid over-fitting?  How did they account for the thinness of data available for extreme values in their calibration method?)  But for now, let’s assume this claim is correct, and that the model is calibrated perfectly:  The fact that teams predicted to win 30% of the time actually won 30% of the time does NOT mean that each team actually had a 30% chance of winning.

That 30% number is just an average.  If you believe that the model perfectly nails the actual expectation for every team, you are crazy.  Since there is a large and reasonably measurable amount of variance in the very small sample of underlying statistics that the predictive model relies on, it necessarily follows that many teams will have significantly under or over-performed statistically relative to their true strength, which will be reflected in the model’s predictions.  The “perfect calibration” of the model only means that the error is well-hidden.

This doesn’t mean that it’s a bad model: like any heuristic, the model may be completely adequate for its intended context.  For example, if you’re going to bet on an individual game, barring any other information, the average of a team’s potential chances should be functionally equivalent to their actual chances.  But if you’re planning to bet on the end-result of a series of games — such as in the divisional round of the NFL playoffs — failing to understand the distribution of error could be very costly.

For example, let’s look at what happens to Minnesota and Arizona’s Super Bowl chances if we assume that the error in their winrates is uniformly distributed in the neighborhood of their predicted winrate:

image

For Minnesota, I created a pool of 11 possible expectations that includes the actual prediction plus teams that were 5% to 25% better or worse.  I did the same for Arizona, but with half the deviation.  The average win prediction for each game remains constant, but the overall chances of winning the Super Bowl change dramatically.  To some of you, the difference between 2% and 1% may not seem like much, but if you could find a casino that would regularly offer you 100-1 on something that is actually a 50-1 shot, you could become very rich very quickly.  Of course, this uniform distribution is a crude one of many conceivable ways that the “hidden error” could be distributed, and I have no particular reason to think it is more accurate than any other.  But one thing should be abundantly clear: the winrate model on which this whole system rests tells us nothing about this distribution either.

The exact structure of this particular error distribution is mostly an empirical matter that can and should invite further study.  But for the purposes of this essay, speculation may suffice.  For example, here is an ad hoc distribution that I thought seemed a little more plausible than a uniform distribution:

image

This table shows the chances of winning the Super Bowl for a generic divisional round playoff team with an average predicted winrate of 35% for each game.  In this scenario, there is a 30% chance (3/10) that the prediction gets it right on the money, a 40% chance that the team is around half as good as predicted (the bottom 4 values), a 10% chance that the team is slightly better, a 10% chance that it is significantly better, and a 10% chance that the model’s prediction is completely off its rocker.  These possibilities still produce a 35% average winrate, yet, as above, the overall chances of winning the Super Bowl increase significantly (this time by almost double).  Of course, 2 random hypothetical distributions don’t yet indicate a trend, so let’s look at a family of distributions to see if we can find any patterns:

image

This chart compares the chances of a team with a given predicted winrate to win the Super Bowl based on uniform error distributions of various sizes.  So the percentages in column 1 are the odds of the team winning the Super Bowl if the predicted winrate is exactly equal to their actual winrate.  Then each subsequent column is the chances of them winning the Superbowl if you increase the “pool” of potential actual winrates by one on each side.  Thus, the second number after 35% is the odds of winning the Super Bowl if the team is equally likely to be have a 30%, 35%, or 40% chance in reality, etc.  The maximum possible change in Super Bowl winning chances for each starting prediction is contained in the light yellow box at the end of each row.  I should note that I chose this family of distributions for its ease of cross-comparison, not its precision.  I also experimented with many other models that produced a variety of interesting results, yet in every even remotely plausible one of them, two trends – both highly germane to my initial criticism of Burke’s model – endured:
1.  Lower predicted game odds lead to greater disparity between predicted and actual chances.
To further illustrate this, here’s a vertical slice of the data, containing the net change for each possible prediction, given a discreet uniform error distribution of size 7:

image

2.  Greater error ranges in the underlying distribution lead to greater disparity between predicted and actual chances.

To further illustrate this, here’s a horizontal slice of the data, containing the net change for each possible error range, given an initial winrate prediction of 35%:

image

Of course these underlying error distributions can and should be examined further, but even at this early stage of inquiry, we “know” enough (at least with a high degree of probability) to begin drawing conclusions.  I.e., We know there is considerable variance in the statistics that Burke’s model relies on, which strongly suggests that there is a considerable amount of “hidden error” in its predictions.  We know greater “hidden error” leads to greater disparity in predicted Super Bowl winning chances, and that this disparity is greatest for underdogs.  Therefore, it is highly likely that this model significantly under-represents the chances of underdog teams at the divisional stage of the playoffs going on to win the Superbowl.  Q.E.D.

This doesn’t mean that these problems aren’t fixable: the nature of the error distribution of the individual game-predicting model could be investigated and modeled itself, and the results could be used to adjust Burke’s playoff predictions accordingly.  Alternatively, if you want to avoid the sticky business of characterizing all that hidden error, a Super-Bowl prediction model could be built that deals with that problem heuristically: say, by running a logistical regression that uses the available data to predict each team’s chances of winning the Super Bowl directly.

Finally, I believe this evidence both directly and indirectly supports my intuition that the large disparity between Burke’s predictions and the corresponding contract prices was more likely to be the result of model error than market error.  The direct support should be obvious, but the indirect support is also interesting:  Though markets can get it wrong just as much or more than any other process, I think that people who “put their money where their mouth is” (especially those with the most influence on the markets) tend to be more reliably skeptical and less dogmatic about making their investments than bloggers, analysts or even academics are about publishing their opinions.  Moreover, by its nature, the market takes a much more pluralistic approach to addressing controversies than do most individuals.  While this may leave it susceptible to being marginally outperformed (on balance) by more directly focused individual models or persons, I think it will also be more likely to avoid pitfalls like the one above.

Conclusions, and My Broader Agenda

The general purpose of post is to demonstrate both the importance and difficulty of understanding and characterizing the ways in which our beliefs – and the processes we use to form them — can get it wrong.  This is, at its heart, a delicate but extremely pragmatic endeavor.  It involves being appropriately skeptical of various conclusions — even when they seem right to you – and recognizing the implications of the multitude of ways that such error can manifest.

I have a whole slew of ideas about how to apply these principles when evaluating the various pronouncements made by the political commentariat, but the blogosphere already has a Nate Silver (and Mr. Silver is smarter than me anyway), so I’ll leave that for you to consider as you see fit.

On Nate Silver on ESPN Umpire Study

I was just watching the Phillies v. Mets game on TV, and the announcers were discussing this Outside the Lines study about MLB umpires, which found that 1 in 5 “close” calls were missed over their 184 game sample.  Interesting, right?

So I opened up my browser to find the details, and before even getting to ESPN, I came across this criticism of the ESPN story by Nate Silver of FiveThirtyEight, which knocks his sometimes employer for framing the story on “close calls,” which he sees as an arbitrary term, rather than something more objective like “calls per game.”  Nate is an excellent quantitative analyst, and I love when he ventures from the murky world of politics and polling to write about sports.  But, while the ESPN study is far from perfect, I think his criticism here is somewhat off-base ill-conceived.

The main problem I have with Nate’s analysis is that the study’s definition of “close call” is not as “completely arbitrary” as Nate suggests.  Conversely, Nate’s suggested alternative metric – blown calls per game – is much more arbitrary than he seems to think.

First, in the main text of the ESPN.com article, the authors clearly state that the standard for “close” that they use is: “close enough to require replay review to determine whether an umpire had made the right call.”  Then in the 2nd sidebar, again, they explicitly define “close calls” as  “those for which instant replay was necessary to make a determination.”  That may sound somewhat arbitrary in the abstract, but let’s think for a moment about the context of this story: Given the number of high-profile blown calls this season, there are two questions on everyone’s mind: “Are these umps blind?” and “Should baseball have more instant replay?” Indeed, this article mentions “replay” 24 times.  So let me be explicit where ESPN is implicit:  This study is about instant replay.  They are trying to assess how many calls per game could use instant replay (their estimate: 1.3), and how many of those reviews would lead to calls being overturned (their estimate: 20%).

Second, what’s with a quantitative (sometimes) sports analyst suddenly being enamored with per-game rather than rate-based stats?  Sure, one blown call every 4 games sounds low, but without some kind of assessment of how many blown call opportunities there are, how would we know?  In his post, Nate mentions that NBA insiders tell him that there were “15 or 20 ‘questionable’ calls” per game in their sport.  Assuming ‘questionable’ means ‘incorrect,’ does that mean NBA referees are 60 to 80 times worse than MLB umpires?  Certainly not.  NBA refs may or may not be terrible, but they have to make double or even triple digit difficult calls every night.  If you used replay to assess every close call in an NBA game, it would never end.  Absent some massive longitudinal study comparing how often officials miss particular types of calls from year to year or era to era, there is going to be a subjective component when evaluating officiating.  Measuring by performance in “close” situations is about as good a method as any.

Which is not to say that the ESPN metric couldn’t be improved:  I would certainly like to see their guidelines for figuring out whether a call is review-worthy or not.  In a perfect world, they might even break down the sets of calls by various proposals for replay implementation.  As a journalistic matter, maybe they should have spent more time discussing their finding that only 1.3 calls per game are “close,” as that seems like an important story in its own right.  On balance, however, when it comes to the two main issues that this study pertains to (the potential impact of further instant replay, and the relative quality of baseball officiating), I think ESPN’s analysis is far more probative than Nate’s.

Hidden Sources of Error—A Back-Handed Defense of Football Outsiders

So I was catching up on some old blog-reading and came across this excellent post by Brian Burke, Pre-Season Predictions Are Still Worthless, showing that the Football Outsiders pre-season predictions are about as accurate as picking 8-8 for every team would be, and that a simple regression based on one variable — 6 wins plus 1/4 of the previous season’s wins — is significantly more accurate

While Brian’s anecdote about Billy Madison humorously skewers Football Outsiders, it’s not entirely fair, and I think these numbers don’t prove as much as they may appear to at first glance.  Sure, a number of conventional or unconventional conclusions people have reached are probably false, but the vast majority of sports wisdom is based on valid causal inferences with at least a grain of truth.  The problem is that people have a tendency to over-rely on the various causes and effects that they observe directly, conversely underestimating the causes they cannot see.

So far, so obvious.  But these “hidden” causes can be broken down further, starting with two main categories, which I’ll call “random causes” and “counter-causes”:

“Random causes” are not necessarily truly random, but do not bias your conclusions in any particular direction.  It is the truly random combined with the may-as-well-be-random, and generates the inherent variance of the system.

“Counter causes” are those which you may not see, but which relate to your variables in ways that counteract your inferences.  The salary cap in the NFL is one of the most ubiquitous offenders:  E.g. an analyst sees a very good quarterback, and for various reasons believes that QB with a particular skill-set is worth an extra 2 wins per season.  That QB is obtained by an 8-8 team in free agency, so the analyst predicts that team will win 10 games.  But in reality, the team that signed that quarterback had to pay handsomely for that +2 addition, and may have had to cut 2 wins worth of players to do it.  If you imagine this process repeating itself over time, you will see that the correlation between QB’s with those skills and their team’s actual winrate may be small or non-existent (in reality, of course, the best quarterbacks are probably underpaid relative to their value, so this is not a problem).  In closed systems like sports, these sorts of scenarios crop up all the time, and thus it is not uncommon for a perfectly valid and logical-seeming inference to be, systematically, dead wrong (by which I mean that it not only leads to an erroneous conclusion in a particular situation, but will lead to bad predictions routinely).

So how does this relate to Football Outsiders, and how does it amount to a defense of their predictions?  First, I think the suggestion that FO may have created “negative knowledge” is demonstrably false:  The key here is not to be fooled by the stat that they could barely beat the “coma patient” prediction of 8-8 across the board.  8 wins is the most likely outcome for any team ex ante, and every win above or below that number is less and less likely.  E.g., if every outcome were the result of a flip of a coin, your best strategy would be to pick 8-8 for every team, and picking *any* team to go 10-6 or 12-4 would be terrible.  Yet Football Outsiders (and others) — based on their expertise — pick many teams to have very good and very bad records.  The fact that they break even against the coma patient shows that their expertise is worth something.

Second, I think there’s no shame in being unable to beat a simple regression based on one extremely probative variable:  I’ve worked on a lot of predictive models, from linear regressions to neural networks, and beating a simple regression can be a lot of work for marginal gain (which, combined with the rake, is the main reason that sports-betting markets can be so tough).

Yet, getting beaten so badly by a simple regression is a definite indicator of systematic error — particularly since there is nothing preventing Football Outsiders from using a simple regression to help them make their predictions. Now, I suspect that FO is underestimating football variance, especially the extent of regression to the mean.  But this is a blanket assumption that I would happily apply to just about any sports analyst — quantitative or not — and is not really of interest.  However, per the distinction I made above, I believe FO is likely underestimating the “counter causes” that may temper the robustness of their inferences without necessarily invalidating them entirely.  A relatively minor bias in this regard could easily lead to a significant drop in overall predictive performance, for the same reason as above:  the best and worst records are by far the least likely to occur.  Thus, *ever* predicting them, and expecting to gain accuracy in the process, requires an enormous amount of confidence.  If Football Outsiders has that degree of confidence, I would wager that it is misplaced.

Player Efficiency Ratings—A Bold ESPN Article Gets it Exactly Wrong

Tom Haberstroh, credited as a “Special to ESPN Insider” in his byline, writes this 16 paragraph article, about how “Carmelo Anthony is not an elite player.” Haberstroh boldly — if not effectively — argues that Carmelo’s high shot volume and correspondingly pedestrian Player Efficiency Rating suggests that not only is ‘Melo not quite the superstar his high scoring average makes him out to be, but that he is not even worth the max contract he will almost certainly get next summer.  Haberstroh further argues that this case is, in fact, a perfect example of why people should stop paying as much attention to Points Per Game and start focusing instead on PER’s.

I have a few instant reactions to this article that I thought I would share:

  1. Anthony may or may not be overrated, and many of Haberstroh’s criticisms on this front are valid — e.g., ‘Melo does have a relatively low shooting percentage — but his evidence is ultimately inconclusive.
  2. Haberstroh’s claim that Anthony is not worth a max contract is not supported at all.  How many players are “worth” max contracts?  The very best players, even with their max contracts, are incredible value for their teams (as evidenced by the fact that they typically win).  Corollary to this, there are almost certainly a number of players who are *not* the very best, who nevertheless receive max contracts, and who still give their teams good value at their price.  (This is not to mention the fact that players like Anthony, even if they are overrated, still sell jerseys, increase TV ratings, and put butts in seats.)
  3. One piece of statistical evidence that cuts against Haberstroh’s argument is that Carmelo has a very solid win/loss +/- with the Nuggets over his career.  With Melo in the lineup, Denver has won 59.9% of their games (308-206), and without him in the lineup over that period, they have won 50% (30-30).  While 10% may not sound like much, it is actually elite and compares favorably to the win/loss +/- of many excellent players, such as Chris Bosh (9.1%, and one of the top PER players in the league) and Kobe Bryant (4.1%).  All of these numbers should be treated with appropriate skepticism due to the small sample sizes, but they do trend accurately.

But the main point I would like to make is that — exactly opposite Haberstrom — I believe Carmelo Anthony is, in fact, a good example of why people should be *more* skeptical of PER’s as the ultimate arbiter of player value. One of the main problems with PER is that it attempts to account for whether a shot’s outcome is good or bad relative to the average shot, but it doesn’t account for whether the outcome is good or bad relative to the average shot taken in context.  The types of shots a player is asked to take vary both dramatically and systematically, and can thus massively bias his PER.  Many “bad” shots, for example, are taken out of necessity: when the clock is winding down and everyone is defended, someone has to chuck it up.  In that situation, “bad” shooting numbers may actually be good, if they are better than what a typical player would have done.  If the various types of shots were distributed equally, this would all average out in the end, and would only be relevant as a matter of precision.  But in reality, certain players are asked to take the bad shot more often that others, and those players are easy enough to find: they tend to be the best players on their teams.

This doesn’t mean I think PER is useless, or irreparably broken.  Among other things, I think it could be greatly improved by incorporating shot-clock data as a proxy to model the expected value of each shot (which I hope to write more about in the future).  However, in its current form it is far from being the robust and definitive metric that many basketball analysts seem to believe.  Points Per Game may be an even more useless metric — theoretically — but at least it’s honest.