Two nights ago, as I was watching cable news and reading various online articles and blog posts about Christine O’Donnell’s upset win over Michael Castle in Delaware’s Republican Senate primary, the hasty, almost ferocious emergence of consensus among the punditocracy – to wit, that the GOP now has virtually zero chance of picking up that seat in November – reminded me of an issue that I’ve wanted to blog about since long before I began blogging in earnest: NFL playoff prediction models.
Specifically, I have been critical of those models that project the likelihood of each surviving team winning the Super Bowl by applying a logistic regression model (i.e., “odds of winning based on past performance”) to each remaining game. In January, I posted a number of comments to this article on Advanced NFL Stats, in which I found it absurd that, with 8 teams left, his model predicted that the Dallas Cowboys had about the same chance of winning the Super Bowl as the Jets, Ravens, Vikings, and Cardinals combined. In the brief discussion, I gave two reasons (in addition to my intuition): first, that these predictions were wildly out of whack with contract prices in sports-betting markets, and second, that I didn’t believe the model sufficiently accounted for “variance in the underlying statistics.” Burke suggested that the first point is explained by a massive epidemic of conjunction-fallacyitis among sports bettors. On its face, I think this is a ridiculous explanation: i.e., does he really believe that the market-movers in sports betting — people who put up hundreds of thousands (if not millions) of dollars of their own money — have never considered multiplying the odds of several games together? Regardless, in this post I will put forth a much better explanation for this disparity than either of us proffered at the time, hopefully mooting that discussion. On my second point, he was more dismissive, though I was being rather opaque (and somehow misspelled “beat” in one reply), so I don’t blame him. However, I do think Burke’s intellectual hubris regarding his model (aka “model hubris”) is notable – not because I have any reason to think Burke is a particularly hubristic individual, but because I think it is indicative of a massive epidemic of model-hubrisitis among sports bloggers.
In Section 1 of this post, I will discuss what I personally mean by “applied epistemology” (with apologies to any actual applied epistemologists out there) and what I think some of its more-important implications are. In Section 2, I will try to apply these concepts by taking a more detailed look at my problems with the above-mentioned playoff prediction models.
Section 1: Applied Epistemology Explained, Sort Of
For those who might not know, “epistemology” is essentially a fancy word for the “philosophical study of knowledge,” which mostly involves philosophers trying to define the word “knowledge” and/or trying to figure out what we know (if anything), and/or how we came to know it (if we do). For important background, read my Complete History of Epistemology (abridged), which can be found here: In Plato’s Theaetetus, Socrates suggests that knowledge is something like “justified true belief.” Agreement ensues. In 1963, Edmund Gettier suggests that a person could be justified in believing something, but it could be true for the wrong reasons. Debate ensues. The End.
A “hot” topic in the field recently has been dealing with the implications of elaborate thought experiments similar to the following:
*begin experiment*
Imagine yourself in the following scenario: From childhood, you have one burning desire: to know the answer to Question X. This desire is so powerful that you dedicate your entire life to its pursuit. You work hard in school, where you excel greatly, and you master every relevant academic discipline, becoming a tenured professor at some random elite University, earning multiple doctorates in the process. You relentlessly refine and hone your (obviously considerable) reasoning skills using every method you can think of, and you gather and analyze every single piece of empirical data relevant to Question X available to man. Finally, after decades of exhaustive research and study, you have a rapid series of breakthroughs that lead you to conclude – not arbitrarily, but completely based on the proof you developed through incredible amounts of hard work and ingenuity — that the answer to Question X is definitely, 100%, without a doubt: 42. Congratulations! To celebrate the conclusion of this momentous undertaking, you decide to finally get out of the lab/house/library and go celebrate, so you head to a popular off-campus bar. You are so overjoyed about your accomplishment that you decide to buy everyone a round of drinks, only to find that some random guy — let’s call him Neb – just bought everyone a round of drinks himself. What a joyous occasion: two middle-aged individuals out on the town, with reason to celebrate (and you can probably see where this is going, but I’ll go there anyway)! As you quickly learn, it turns out that Neb is around your same age, and is also a professor at a similarly elite University in the region. In fact, it’s amazing how much you two have in common: you have relatively similar demographic histories, identical IQ, SAT, and GRE scores, you both won multiple academic awards at every level, you have both achieved similar levels of prominence in your academic community, and you have both been repeatedly published in journals of comparable prestige. In fact, as it turns out, you have both been spent your entire lives studying the same question! You have both read all the same books, you have both met, talked or worked with many comparably intelligent — or even identical — people: It is amazing that you have never met! Neb, of course, is feeling so celebratory because finally, after decades of exhaustive research and study, he has just had a rapid series of breakthroughs that lead him to finally conclude – not arbitrarily, but completely based on the proof he developed through incredible amounts of hard work and ingenuity — that the answer to Question X is definitely, 100%, without a doubt: 54.
You spend the next several hours drinking and arguing about Question X: while Neb seemed intelligent enough at first, everything he says about X seems completely off base, and even though you make several excellent points, he never seems to understand them. He argues from the wrong premises in some areas, and draws the wrong conclusions in others. He massively overvalues many factors that you are certain are not very important, and is dismissive of many factors that you are certain are crucial. His arguments, though often similar in structure to your own, are extremely unpersuasive and don’t seem to make any sense, and though you try to explain yourself to him, he stubbornly refuses to comprehend your superior reasoning. The next day, you stumble into class, where your students — who had been buzzing about your breakthrough all morning — begin pestering you with questions about Question X and 42. In your last class, you had estimated that the chances of 42 being “the answer” were around 90%, and obviously they want to know if you have finally proved 42 for certain, and if not, how likely you believe it is now. What do you tell them?
All of the research and analysis you conducted since your previous class had, indeed, led you to believe that 42 is a mortal lock. In the course of your research, everything you have thought about or observed or uncovered, as well as all of the empirical evidence you have examined or thought experiments you have considered, all lead you to believe that 42 is the answer. As you hesitate, your students wonder why, even going so far as to ask, “Have you heard any remotely persuasive arguments against 42 that we should be considering?” Can you, in good conscience, say that you know the answer to Question X? For that matter, can you even say that the odds of 42 are significantly greater than 50%? You may be inclined, as many have been, to “damn the torpedoes” and act as if Neb’s existence is irrelevant. But that view is quickly rebutted: Say one of your most enterprising students brings a special device to class: when she presses the red button marked “detonate,” if the answer to Question X is actually 42, the machine will immediately dispense $20 bills for everyone in the room; but if the answer is not actually 42, it will turn your city into rubble. And then it will search the rubble, gather any surviving puppies or kittens, and blend them.
So assuming you’re on board that your chance encounter with Professor Neb implies that, um, you might be wrong about 42, what comes next? There’s a whole interesting line of inquiry about what the new likelihood of 42 is and whether anything higher than 50% is supportable, but that’s not especially relevant to this discussion. But how about this: Say the scenario proceeds as above, you dedicate your life, yadda yadda, come to be 100% convinced of 42, but instead of going out to a bar, you decide to relax with a bubble bath and a glass of Pinot, while Neb drinks alone. You walk into class the next day, and proudly announce that the new odds of 42 are 100%. Mary Kate pulls out her special money-dispensing device, and you say sure, it’s a lock, press the button. Yay, it’s raining Andrew Jacksons in your classroom! And then: **Boom** **Meow** **Woof** **Whirrrrrrrrrrrrrr**. Apparently Mary Kate had a twin sister — she was in Neb’s class.
*end experiment*
In reality, the fact that you might be wrong, even when you’re so sure you’re right, is more than a philosophical curiosity, it is a mathematical certainty. The processes that lead you to form beliefs, even extremely strong ones, are imperfect. And when you are 100% certain that a belief-generating process is reliable, the process that led you to that belief is likely imperfect. This line of thinking is sometimes referred to as skepticism — which would be fine if it weren’t usually meant as a pejorative.
When push comes to shove, people will usually admit that there is at least some chance they are wrong, yet they massively underestimate just what those chances are. In political debates, for example, people may admit that there is some miniscule possibility that their position is ill-informed or empirically unsound, but they will almost never say that they are more likely to be wrong than to be right. Yet, when two populations hold diametrically opposed views, either one population is wrong or both are – all else being equal, the correct assessment in such scenarios is that no-one is likely to have it right.
When dealing with beliefs about probabilities, the complications get even trickier: Obviously many people believe some things are close to 100% likely to be true, when the real probability may be some-much if not much-much lower. But in addition to the extremes, people hold a whole range of poorly-calibrated probabilistic beliefs, like believing something is 60% likely when it is actually 50% or 70%. (Note: Some Philosophically trained readers may balk at this idea, suggesting that determinism entails everything having either a 0 or 100% probability of being true. While this argument may be sound in classroom discussions, it is highly unpragmatic: If I believe that I will win a coin flip 60% of the time, it may be theoretically true that the universe has already determined whether the coin will turn up heads or tails, but for all intents and purposes, I am only wrong by 10%).
But knowing that we are wrong so much of the time doesn’t tell us much by itself: it’s very hard to be right, and we do the best we can. We develop heuristics that tend towards the right answers, or — more importantly for my purposes — that allow the consequences of being wrong in both directions even out over time. You may reasonably believe that the probability of something is 30%, when, in reality, the probability is either 20% or 40%. If the two possibilities are equally likely, then your 30% belief may be functionally equivalent under many circumstances, but they are not the same, as I will demonstrate in Section 2 (note to the philosophers: you may have noticed that this is a bit like the Gettier examples: you might be “right,” but for the wrong reasons).
There is a science to being wrong, and it doesn’t mean you have to mope in your study, or act in bad faith when you’re out of it. “Applied Epistemology” (at least as this armchair philosopher defines it) is the study of the processes that lead to knowledge and beliefs, and of the practical implications of their limitations.
Part 2: NFL Playoff Prediction Models
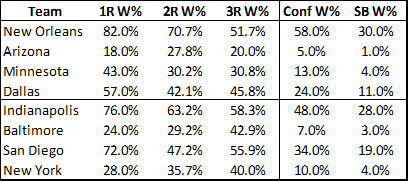
Now, let’s finally return to the Advanced NFL Stats playoff prediction model. Burke’s methodology is simple: using a logistic regression based on various statistical indicators, the model estimates a probability for each team to win their first round matchup. It then repeats the process for all possible second round matchups, weighting each by its likelihood of occurring (as determined by the first round projections) and so on through the championship. With those results in hand, a team’s chances of winning the tournament is simply the product of their chances of winning in each round. With 8 teams remaining in the divisional stage, the model’s predictions looked like this:
Burke states that the individual game prediction model has a “history of accuracy” and is well “calibrated,” meaning that, historically, of the teams it has predicted to win 30% of the time, close to 30% of them have won, and so on. For a number of reasons, I remain somewhat skeptical of this claim, especially when it comes to “extreme value” games where the model predicts very heavy favorites or underdogs. (E.g’s: What validation safeguards do they deploy to avoid over-fitting? How did they account for the thinness of data available for extreme values in their calibration method?) But for now, let’s assume this claim is correct, and that the model is calibrated perfectly: The fact that teams predicted to win 30% of the time actually won 30% of the time does NOT mean that each team actually had a 30% chance of winning.
That 30% number is just an average. If you believe that the model perfectly nails the actual expectation for every team, you are crazy. Since there is a large and reasonably measurable amount of variance in the very small sample of underlying statistics that the predictive model relies on, it necessarily follows that many teams will have significantly under or over-performed statistically relative to their true strength, which will be reflected in the model’s predictions. The “perfect calibration” of the model only means that the error is well-hidden.
This doesn’t mean that it’s a bad model: like any heuristic, the model may be completely adequate for its intended context. For example, if you’re going to bet on an individual game, barring any other information, the average of a team’s potential chances should be functionally equivalent to their actual chances. But if you’re planning to bet on the end-result of a series of games — such as in the divisional round of the NFL playoffs — failing to understand the distribution of error could be very costly.
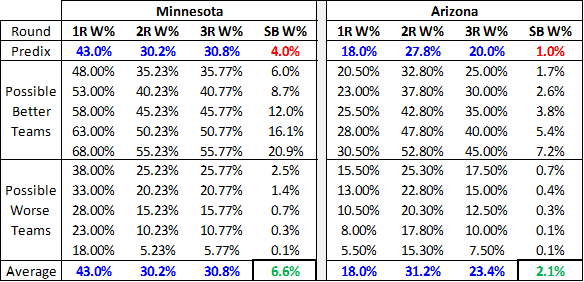
For example, let’s look at what happens to Minnesota and Arizona’s Super Bowl chances if we assume that the error in their winrates is uniformly distributed in the neighborhood of their predicted winrate:
For Minnesota, I created a pool of 11 possible expectations that includes the actual prediction plus teams that were 5% to 25% better or worse. I did the same for Arizona, but with half the deviation. The average win prediction for each game remains constant, but the overall chances of winning the Super Bowl change dramatically. To some of you, the difference between 2% and 1% may not seem like much, but if you could find a casino that would regularly offer you 100-1 on something that is actually a 50-1 shot, you could become very rich very quickly. Of course, this uniform distribution is a crude one of many conceivable ways that the “hidden error” could be distributed, and I have no particular reason to think it is more accurate than any other. But one thing should be abundantly clear: the winrate model on which this whole system rests tells us nothing about this distribution either.
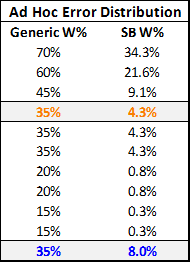
The exact structure of this particular error distribution is mostly an empirical matter that can and should invite further study. But for the purposes of this essay, speculation may suffice. For example, here is an ad hoc distribution that I thought seemed a little more plausible than a uniform distribution:
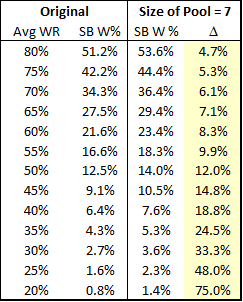
This table shows the chances of winning the Super Bowl for a generic divisional round playoff team with an average predicted winrate of 35% for each game. In this scenario, there is a 30% chance (3/10) that the prediction gets it right on the money, a 40% chance that the team is around half as good as predicted (the bottom 4 values), a 10% chance that the team is slightly better, a 10% chance that it is significantly better, and a 10% chance that the model’s prediction is completely off its rocker. These possibilities still produce a 35% average winrate, yet, as above, the overall chances of winning the Super Bowl increase significantly (this time by almost double). Of course, 2 random hypothetical distributions don’t yet indicate a trend, so let’s look at a family of distributions to see if we can find any patterns:
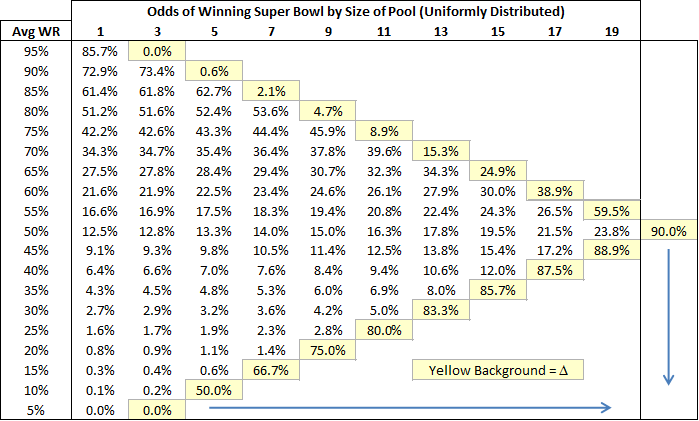
This chart compares the chances of a team with a given predicted winrate to win the Super Bowl based on uniform error distributions of various sizes. So the percentages in column 1 are the odds of the team winning the Super Bowl if the predicted winrate is exactly equal to their actual winrate. Then each subsequent column is the chances of them winning the Superbowl if you increase the “pool” of potential actual winrates by one on each side. Thus, the second number after 35% is the odds of winning the Super Bowl if the team is equally likely to be have a 30%, 35%, or 40% chance in reality, etc. The maximum possible change in Super Bowl winning chances for each starting prediction is contained in the light yellow box at the end of each row. I should note that I chose this family of distributions for its ease of cross-comparison, not its precision. I also experimented with many other models that produced a variety of interesting results, yet in every even remotely plausible one of them, two trends – both highly germane to my initial criticism of Burke’s model – endured:
1. Lower predicted game odds lead to greater disparity between predicted and actual chances.
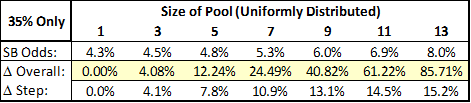
To further illustrate this, here’s a vertical slice of the data, containing the net change for each possible prediction, given a discreet uniform error distribution of size 7:
2. Greater error ranges in the underlying distribution lead to greater disparity between predicted and actual chances.
To further illustrate this, here’s a horizontal slice of the data, containing the net change for each possible error range, given an initial winrate prediction of 35%:
Of course these underlying error distributions can and should be examined further, but even at this early stage of inquiry, we “know” enough (at least with a high degree of probability) to begin drawing conclusions. I.e., We know there is considerable variance in the statistics that Burke’s model relies on, which strongly suggests that there is a considerable amount of “hidden error” in its predictions. We know greater “hidden error” leads to greater disparity in predicted Super Bowl winning chances, and that this disparity is greatest for underdogs. Therefore, it is highly likely that this model significantly under-represents the chances of underdog teams at the divisional stage of the playoffs going on to win the Superbowl. Q.E.D.
This doesn’t mean that these problems aren’t fixable: the nature of the error distribution of the individual game-predicting model could be investigated and modeled itself, and the results could be used to adjust Burke’s playoff predictions accordingly. Alternatively, if you want to avoid the sticky business of characterizing all that hidden error, a Super-Bowl prediction model could be built that deals with that problem heuristically: say, by running a logistical regression that uses the available data to predict each team’s chances of winning the Super Bowl directly.
Finally, I believe this evidence both directly and indirectly supports my intuition that the large disparity between Burke’s predictions and the corresponding contract prices was more likely to be the result of model error than market error. The direct support should be obvious, but the indirect support is also interesting: Though markets can get it wrong just as much or more than any other process, I think that people who “put their money where their mouth is” (especially those with the most influence on the markets) tend to be more reliably skeptical and less dogmatic about making their investments than bloggers, analysts or even academics are about publishing their opinions. Moreover, by its nature, the market takes a much more pluralistic approach to addressing controversies than do most individuals. While this may leave it susceptible to being marginally outperformed (on balance) by more directly focused individual models or persons, I think it will also be more likely to avoid pitfalls like the one above.
Conclusions, and My Broader Agenda
The general purpose of post is to demonstrate both the importance and difficulty of understanding and characterizing the ways in which our beliefs – and the processes we use to form them — can get it wrong. This is, at its heart, a delicate but extremely pragmatic endeavor. It involves being appropriately skeptical of various conclusions — even when they seem right to you – and recognizing the implications of the multitude of ways that such error can manifest.
I have a whole slew of ideas about how to apply these principles when evaluating the various pronouncements made by the political commentariat, but the blogosphere already has a Nate Silver (and Mr. Silver is smarter than me anyway), so I’ll leave that for you to consider as you see fit.