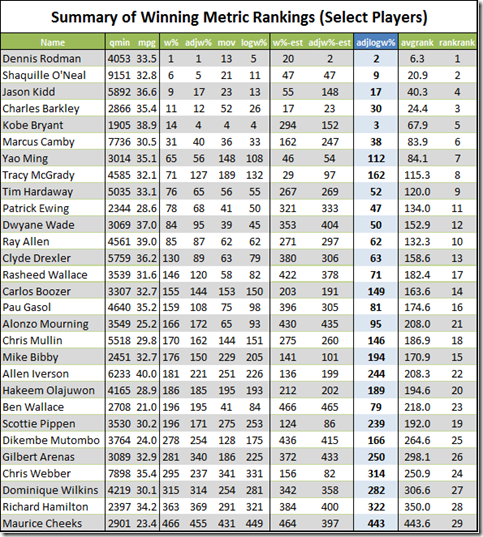
[ADDED: Unsurpisingly, this post has been getting a lot of traffic, which I assume includes a number of new readers who are unfamiliar with my “Case For Dennis Rodman.” So, for the uninitiated, I’d like to (at least temporarily) repeat a few of my late-comer intro points from Part 4(a): “The main things you need to know about this series are that it’s 1) extremely long (sprawling over 13 sections in 4 parts), 2) ridiculously (almost comically) detailed, and 3) only partly about Dennis Rodman. There is a lot going on, so to help new and old readers alike, I have a newly-updated “Rodman Series Guide,” which includes a broken down list of articles, a sampling of some of the most important graphs and visuals, and a giant table summarizing the entire series by post, including the main points on both sides of the analysis.”]
So it comes down to this: With Rodman securely in the Hall of Fame, and his positive impact conclusively demonstrated by the most skeptical standards of proof I can muster, what more is there to say? Repeatedly, my research on Rodman has led to unexpectedly extreme discoveries: Rodman was not just a great rebounder, but the greatest of all time—bar none. And despite playing mostly for championship contenders, his differential impact on winning was still the greatest measured of any player with data even remotely as reliable as his. The least generous interpretation of the evidence still places Rodman’s value well within the realm of the league’s elite, and in Part 4(a) I explored some compelling reasons why the more generous interpretation may be the most plausible.
Yet even that more generous position has its limitations. Though the pool of players I compared with Rodman was broadly representative of the NBA talent pool on the whole, it lacked a few of the all-time greats—in particular, the consensus greatest: Michael Jordan. Due to that conspicuous absence, as well as to the considerable uncertainty of a process that is better suited to proving broad value than providing precise individual ratings, I have repeatedly reminded my readers that, even though Rodman kept topping these lists and metrics, I did NOT mean to suggest that Rodman was actually greater than the greatest of them all. In this final post of this series, I will consider the opposite position: that there is a plausible argument (with evidence to back it up) that Rodman’s astounding win differentials—even taken completely at face value—may still understate his true value by a potentially game-changing margin.
A Dialogue:
First off, this argument was supposed to be an afterthought. Just a week ago—when I thought I could have it out the next morning—it was a few paragraphs of amusing speculation. But, as often seems to be the case with Dennis Rodman-related research, my digging uncovered a bit more than I expected.
The main idea has its roots in a conversation I had (over bruschetta) with a friend last summer. This friend is not a huge sports fan, nor even a huge stats geek, but he has an extremely sharp analytical mind, and loves, loves to tear apart arguments—and I mean that literally: He has a Ph.D. in Rhetoric. In law school, he was the guy who annoyed everyone by challenging almost everything the profs ever said—and though I wouldn’t say he was usually right, I would say he was usually onto something.
That night, I was explaining my then-brand new “Case for Dennis Rodman” project, which he was naturally delighted to dissect and criticize. After painstakingly laying out most of The Case—of course having to defend and explain many propositions that I had been taking for granted and needing to come up with new examples and explanations on the fly, just to avoid sounding like an idiot (seriously, talking to this guy can be intense)—I decided to try out this rhetorical flourish that made a lot of sense to me intuitively, but which had never really worked for anyone previously:
“Let me put it this way: Rodman was by far the best third-best player in NBA History.”
As I explained, “third best” in this case is sort of a term of art, not referring to quality, but to a player’s role on his team. I.e., not the player a team is built around (1st best), or even the supporting player in a “dynamic duo” (like HOF 2nd-besters Scotty Pippen or John Stockton), but the guy who does the dirty work, who mostly gets mentioned in contexts like, “Oh yeah, who else was on that [championship] team? Oh that’s right, Dennis Rodman”).
“Ah, so how valuable is the best third-best player?”
At the time, I hadn’t completely worked out all of the win percentage differentials and other fancy stats that I would later on, but I had done enough to have a decent sense of it:
“Well, it’s tough to say when it’s hard to even define ‘third-best’ player, but [blah blah, ramble ramble, inarticulate nonsense] I guess I’d say he easily had 1st-best player value, which [blah blah, something about diminishing returns, blah blah] . . . which makes him the best 3rd-best player by a wide margin”.
“How wide?”
“Well, it’s not like he’s as valuable as Michael Jordan, but he’s the best 3rd-best player by a wider margin than Jordan was the best 1st-best player.”
“So you’re saying he was better than Michael Jordan.”
“No, I’m not saying that. Michael Jordan was clearly better.”
“OK, take a team with Michael Jordan and Dennis Rodman on it. Which would hurt them more, replacing Michael Jordan with the next-best primary scoring option in NBA history, or replacing Rodman with the next-best defender/rebounder in NBA history?”
“I’m not sure, but probably Rodman.”
“So you’re saying a team should dump Michael Jordan before it should dump Dennis Rodman?”
“Well, I don’t know for sure, I’m not sure exactly how valuable other defender-rebounders are, but regardless, it would be weird to base the whole argument on who happens to be the 2nd-best player. I mean, what if there were two Michael Jordan’s, would that make him the least valuable starter on an All-Time team?”
“Well OK, how common are primary scoring options that are in Jordan’s league value-wise?”
“There are none, I’m pretty sure he has the most value.”
“BALLPARK.”
“I dunno, there are probably between 0 and 2 in the league at any given time.”
“And how common are defender/rebounder/dirty workers that are in Rodman’s league value-wise?”
“There are none.”
“BALLPARK.”
“There are none. Ballpark.”
“So, basically, if a team had Michael Jordan and Dennis Rodman on it, and they could replace either with some random player ‘in the ballpark’ of the next-best player for their role, they should dump Jordan before they dump Rodman?”
“Maybe. Um. Yeah, probably.”
“And I assume that this holds for anyone other than Jordan?”
“I guess.”
“So say you’re head-to-head with me and we’re drafting NBA All-Time teams, you win the toss, you have first pick, who do you take?”
“I don’t know, good question.”
“No, it’s an easy question. The answer is: YOU TAKE RODMAN. You just said so.”
“Wait, I didn’t say that.”
“O.K., fine, I get the first pick. I’ll take Rodman. . . Because YOU JUST TOLD ME TO.”
“I don’t know, I’d have to think about it. It’s possible.”
Up to this point, I confess, I’ve had to reconstruct the conversation to some extent, but these last two lines are about as close to verbatim as my memory ever gets:
“So there you go, Dennis Rodman is the single most valuable player in NBA History. There’s your argument.”
“Dude, I’m not going to make that argument. I’d be crucified. Maybe, like, in the last post. When anyone still reading has already made up their mind about me.”
And that’s it. Simple enough, at first, but I’ve thought about this question a lot between last summer and last night, and it still confounds me: Could being the best “3rd-best” player in NBA history actually make Rodman the best player in NBA history? For starters, what does “3rd-best” even mean? The argument is a semantic nightmare in its own right, and an even worse nightmare to formalize well enough to investigate. So before going there, let’s take a step back:
The Case Against Dennis Rodman:
At the time of that conversation, I hadn’t yet done my league-wide study of differential statistics, so I didn’t know that Rodman would end up having the highest I could find. In fact, I pretty much assumed (as common sense would dictate) that most star-caliber #1 players with a sufficient sample size would rank higher: after all, they have a greater number of responsibilities, they handle the ball more often, and should thus have many more opportunities for their reciprocal advantage over other players to accumulate. Similarly, if a featured player can’t play—potentially the centerpiece of his team, with an entire offense designed around him and a roster built to supplement him—you would think it would leave a gaping hole (at least in the short-run) that would be reflected heavily in his differentials. Thus, I assumed that Rodman probably wouldn’t even “stat out” as the best Power Forward in the field, making this argument even harder to sell. But as the results revealed, it turns out feature players are replaceable after all, and Rodman does just fine on his own. However, there are a couple of caveats to this outcome:
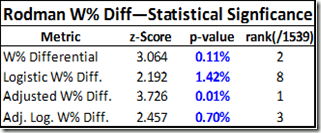
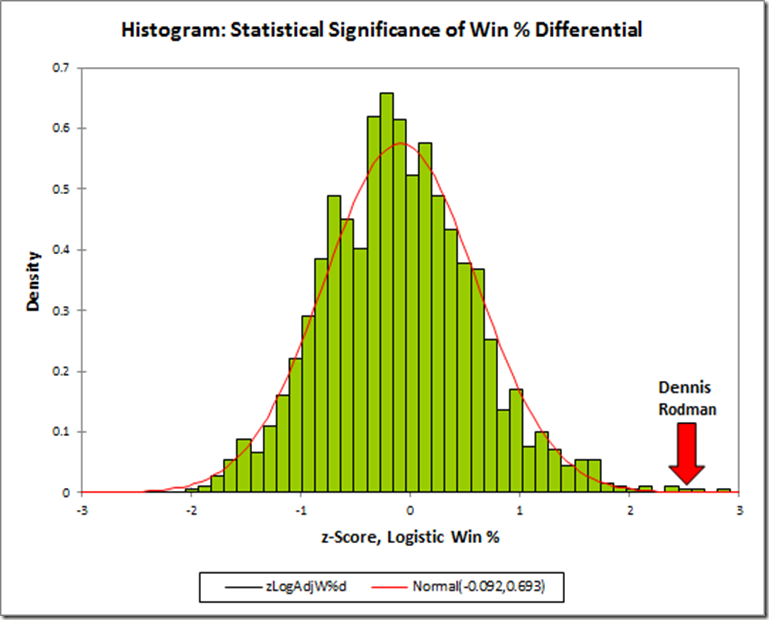
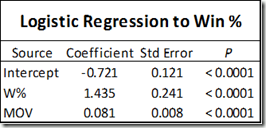
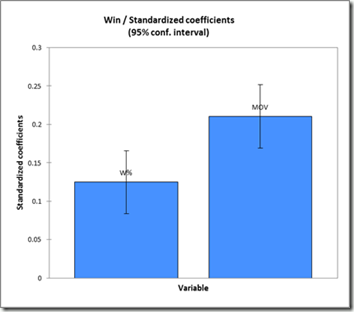
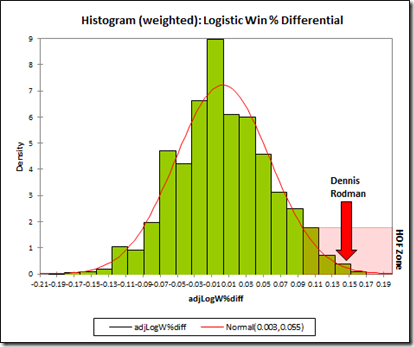
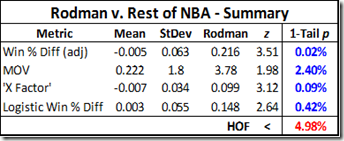
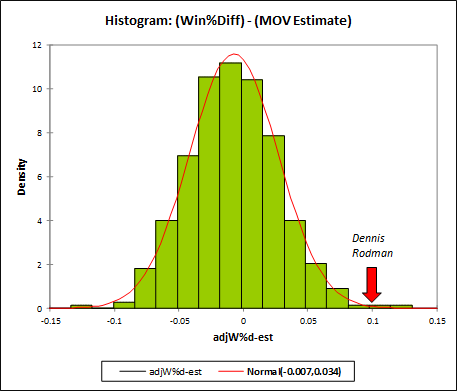
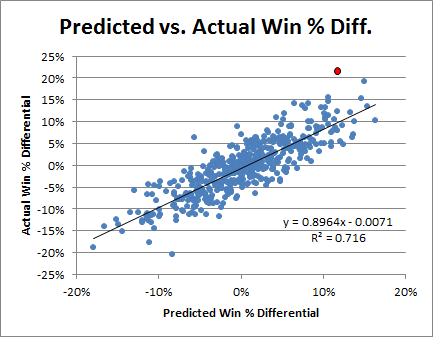
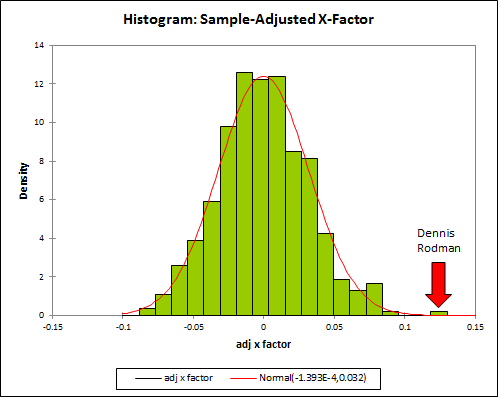
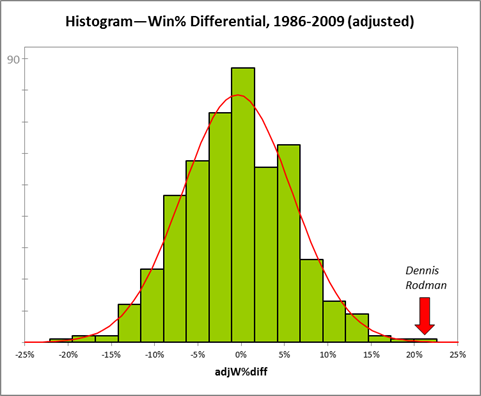
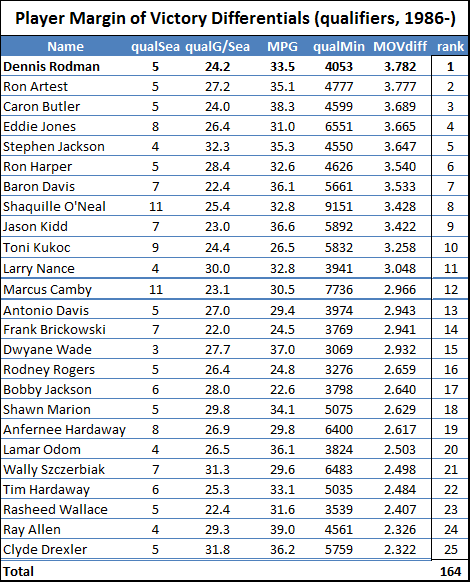
First, without much larger sample sizes, I wouldn’t say that game-by-game win differentials are precise enough to settle disputes between players of similar value. For example, the standard deviation for Rodman’s 22% adjusted win differential is still 5% (putting him less than a full standard deviation above some of the competition). This is fine for concluding that he was extremely valuable, but it certainly isn’t extreme enough to outright prove the seemingly farfetched proposition that he was actually the most valuable player overall. The more unlikely you believe that proposition to be, the less you should find this evidence compelling—this is a completely rational application of Bayes’ Theorem—and I’m sure most of you, ex ante, find the proposition very very unlikely. Thus, to make any kind of argument for Rodman’s superiority that anyone but the biggest Rodman devotees would find compelling, we clearly need more than win differentials.
Second, it really is a shame that a number of the very best players didn’t qualify for the study—particularly the ultimate Big Three: Michael Jordan, Magic Johnson, and Larry Bird (who, in maybe my favorite stat ever, never had a losing month in his entire career). As these three are generally considered to be in a league of their own, I got the idea: if we treated them as one player, would their combined sample be big enough to make an adequate comparison? Well, I had to make a slight exception to my standard filters to allow Magic Johnson’s 1987 season into the mix, but here are the results:
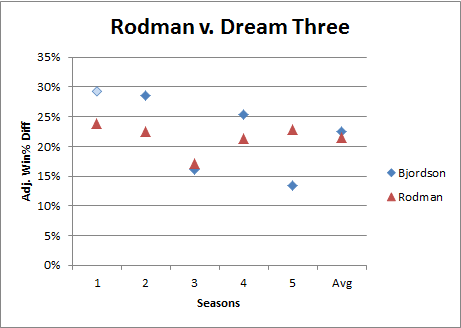
Adjusted Win percentage differential is Rodman’s most dominant value stat, and here, finally, Herr Bjordson edges him. Plus this may not fully represent these players’ true strength: the two qualifying Jordan seasons are from his abrupt return in 1994 and his first year with the Wizards in 2001, and both of Bird’s qualifying seasons are from the last two of his career, when his play may have been hampered by a chronic back injury. Of course, just about any more-conventional player valuation system would rank these players above (or way above) Rodman, and even my own proprietary direct “all-in-one” metric puts these three in their own tier with a reasonable amount of daylight between them and the next pack (which includes Rodman) below. So despite having a stronger starting position in this race than I would have originally imagined, I think it’s fair to say that Rodman is still starting with a considerable disadvantage.
Trade-offs and Invisible Value:
So let’s assume that at least a few players offer more direct value than Dennis Rodman. But building a Champion involves more than putting together a bunch of valuable players: to maximize your chances of success, you must efficiently allocate a variety of scare resources, to obtain as much realized value as possible, through a massively complicated set of internal and external constraints.
For example, league rules may affect how much money you can spend and how many players you can carry on your roster. Game rules dictate that you only have so many players on the floor at any given time, and thus only have so many minutes to distribute. Strategic realities require that certain roles and responsibilities be filled: normally, this means you must have a balance of talented players who play different positions—but more broadly, if you hope to be successful, your team must have the ability to score, to defend, to rebound, to run set plays, to make smart tactical maneuvers, and to do whatever else that goes into winning. All of these little things that your team has to do can also be thought of as a limited resource: in the course of a game, you have a certain number of things to be done, such as taking shots, going after loose balls, setting up a screens, contesting rebounds, etc. Maybe there are 500 of these things, maybe 1000, who knows, but there are only so many to go around—and just as with any other scarce resource, the better teams will be the ones that squeeze the most value out of each opportunity.
Obviously, some players are better at some things than others, and may contribute more in some areas than others—but there will always be trade-offs. No matter how good you are, you will always occupy a slot on the roster and a spot on the floor, every shot you take or every rebound you get means that someone else can’t take that shot or get that rebound, and every dollar your team spends on you is a dollar they can’t spend on someone else. Thus, there are two sides to a player’s contribution: how much surplus value he provides, and how much of his team’s scarce resources he consumes.
The key is this: While most of the direct value a player provides is observable, either directly (through box scores, efficiency ratings, etc.) or indirectly (Adjusted +/-, Win Differentials), many of his costs are concealed.
Visible v. Invisible Effects
Two players may provide seemingly identical value, but at different costs. In very limited contexts this can be extremely clear: thought it took a while to catch on, by now all basketball analysts realize that scoring 25 points per game on 20 shots is better than scoring 30 points a game on 40 shots. But in broader contexts, it can be much trickier. For example, with a large enough sample size, Win Differentials should catch almost anything: everything good that a player does will increase his team’s chances of winning when he’s on the floor, and everything bad that he does will decrease his team’s chances of losing when he’s not. Shooting efficiency, defense, average minutes played, psychological impact, hustle, toughness, intimidation—no matter how abstract the skill, it should still be reflected in the aggregate.
No matter how hard the particular skill (or weakness) is to identify or understand, if its consequences would eventually impact a player’s win differentials, (for these purposes) its effects are visible.
But there are other sources of value (or lack thereof) which won’t impact a player’s win differentials—these I will call “invisible.” Some are obvious, and some are more subtle:
Example 1: Money
“Return on Investment” is the prototypical example of invisible value, particularly in a salary-cap environment, where every dollar you spend on one player is a dollar you can’t spend on another. No matter how good a player is, if you give up more to get him than you get from him in return, your team suffers. Similarly, if you can sign a player for much less than he is worth, he may help your team more than other (or even better) players who would cost more money.
This value is generally “invisible” because the benefit that the player provides will only be realized when he plays, but the cost (in terms of limiting salary resources) will affect his team whether he is in the lineup or not. And Dennis Rodman was basically always underpaid (likely because the value of his unique skillset wasn’t fully appreciated at the time):
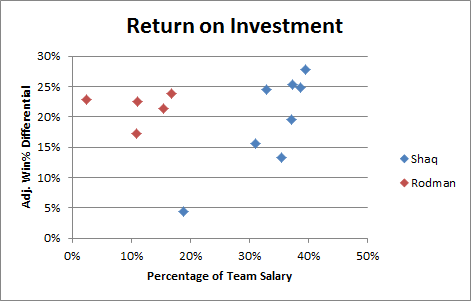
Note: For a fair comparison, this graph (and the similar one below) includes only the 8 qualifying Shaq seasons from before he began to decline.
Aside from the obvious, there are actually a couple of interesting things going on in this graph that I’ll return to later. But I don’t really consider this a primary candidate for the “invisible value” that Rodman would need to jump ahead of Jordan, primarily for two reasons:
First, return on investment isn’t quite as important in the NBA as it is in some other sports: For example, in the NFL, with 1) so many players on each team, 2) a relatively hard salary cap (when it’s in place, anyway), and 3) no maximum player salaries, ROI is perhaps the single most important consideration for the vast majority of personnel decisions. For this reason, great NFL teams can be built on the backs of many underpaid good-but-not-great players (see my extended discussion of fiscal strategy in major sports here).
Second, as a subjective matter, when we judge a player’s quality, we don’t typically consider factors that are external to their actual athletic attributes. For example, a great NFL quarterback could objectively hurt his team if he is paid too much, but we still consider him great. When we ask “who’s the best point guard in the NBA,” we don’t say, “IDK, how much more does Chris Paul get paid than Jason Kidd?” Note this is basically a social preference: It’s conceivable that in some economically-obsessed culture, this sort of thing really would be the primary metric for player evaluation. But personally, and for the purposes of my argument, I prefer our more traditional values on this one.
Example 2: Position
In the “perfect timing” department, a commenter “Siddy Hall” recently raised a hypothetical very similar to my friend’s:
You get 8 people in a room, all posing as GM’s. We’re allowed to select 5 players each from the entire history of the NBA. Then we’ll have a tournament. At PF, I would grab Rodman. And I’m confident that I’d win because he’s on my team. He’d dominate the glass and harass and shutdown a superstar. I think he’s the finest PF to ever play the game.
Of course, you need to surround him with some scorers, but when is that ever a problem?
The commenter only explicitly goes so far as to say that Rodman would be the most valuable power forward. Yet he says he is “confident” that he would win, with the only caveat being that his team gets other scorers (which is a certainty). So, he thinks Rodman is the best PF by a wide enough margin that his team would be a favorite against the team that got Michael Jordan. Let me play the role of my friend above: whether he means to or not, he’s basically saying that Rodman is more valuable than Jordan.
In this example, “position” is the scarce resource. Just as a player can be valuable for the amount of money the team must spend on him, he can also be valuable for his position. But this value can be visible, invisible, or both.
This is probably easiest to illustrate in the NFL, where positions and responsibilities are extremely rigid. An example I used in response to the commenter is that an NFL kicker who could get you 2 extra wins per season could be incredibly valuable. These two extra wins obviously have visible value: By definition, this is a player for whom we would expect to observe a 2 game per season win differential. But there’s another, very important way in which this player’s value would be much greater. As I said in response to the commenter, a +2 kicker could even be more valuable than a +4 quarterback.
In order to play the 2 win kicker, the only cost is your kicker slot, which could probably only get you a fraction of a win even if you had one of the best in the league on your team (relevant background note: kickers normally don’t contribute much, particularly since bad kickers likely influence their teams to make better tactical decisions, and vice-versa). But to play a 4-win quarterback, the cost is your quarterback slot. While the average QB and the average kicker are both worth approximately 0 games, good quarterbacks are often worth much more, and good kickers are worth very little.
Put most simply, because there are no other +2 kickers, that kicker could get 2 wins for virtually ANY team. The +4 QB would only provide 2 wins for teams who would be unable to acquire a +2 quarterback by other means. Or you can think about it conversely: Team A signs the kicker, and Team B signs the QB. For the moment, Team B might appear better, but the most value they will ever be able to get out of their QB/Kicker tandem is +4 games plus epsilon. Team A, on the other hand, can get more value out of their QB/kicker combo than Team B simply by signing any QB worth +2 or greater, who are relatively common.
Why does this matter? Well, in professional sports, we care about one thing more than any other: championships. Teams that win championships do so by having the best roster with the most value. Players like our special kicker provide unique avenues to surplus value that even great other players can’t.
To generalize a bit, you could say that value vs. a replacement player is generally visible, as it will be represented in win differentials no matter who you play for. But a player’s value relative to the entire distribution of players at his position can lead to substantial invisible benefits, as it can substantially improve his team’s ability to build a championship contender.
Formalizing “I-Factor”
Unfortunately, in basketball, such distinctions are much more nebulous. Sure, there are “positions,” but the spot where you line up on the floor is very different from the role you play. E.g., your primary scoring responsibilities can come from any position. And even then “roles” are dynamic and loosely defined (if at all)—some roles that are crucial to certain teams don’t even exist on others. Plus, teams win in different ways: you can do it by having 5 options on offense with 5 guys that can do everything (OK, this doesn’t happen very often, but the Pistons did it in 03-04), or you can be highly specialized and try to exploit the comparative advantages between your players (this seems to be the more popular model of late).
Rodman was a specialist. He played on teams that, for the most part, didn’t ask him to do more than what he was best at—and that probably helped him fully leverage his talents. But the truly amazing part is how much of a consistent impact he could have, on such a variety of different teams, and with seemingly so few responsibilities.
So let’s posit a particular type of invisible value and call it “I-Factor,” with the following elements:
- It improves your team’s chances of building a championship contender.
- It wouldn’t be reflected in your game-to-game win differential.
- It stems from some athletic or competitive skill or attribute.
In the dialogue above, I suggested that Rodman had an inordinate positive impact for a “3rd-best” player, and my friend suggested (insisted really) that this alone should vault him above great but more ordinary “1st-best” players, even if they had significantly more observable impact. Putting these two statements together, we have an examinable hypothesis: That Dennis Rodman’s value relative to his role constituted a very large “I-Factor.”
Evaluating the Hypothesis:
Because the value we’re looking for is (by definition) invisible, its existence is ridiculously hard—if not impossible—to prove empirically (which is why this argument is the dessert instead of the main course of this series).
However, there could be certain signs and indicators we can look for that would make the proposition more likely: specifically, things that would seem unusual or unlikely if the hypothesis were false, but which could be explainable either as causes or effects of the hypothesis being true.
Since the hypothesis posits both an effect (very large I-Factor), and a cause (unusually high value for his role), we should primarily be on the lookout for two things: 1) any interesting or unusual patterns that could be explainable as a consequence of Rodman having a large I-Factor, and 2) any interesting or unusual anomalies that could help indicate that Rodman had an excessive amount of value for his role.
Evidence of Effect:
To lighten the mood a bit, let’s start this section off with a riddle:
Q. What do you get for the team that has everything?
A. Dennis Rodman.
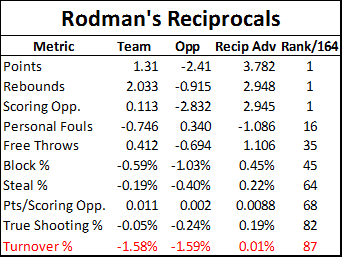
Our hypothetical Rodman I-Factor is much like that of our hypothetical super-kicker in the NFL example above. The reason that kicker was even more valuable than the 2 wins per season he could get you is that he could get those 2 wins for anyone. Normally, if you have a bunch of good players and you add more good players, the whole is less than the sum of its parts. In the sports analytics community, this is generally referred to as “diminishing returns.” An extremely simple example goes like this: Having a great quarterback on your team is great. Having a second great quarterback is maybe mildly convenient. Having a third great quarterback is a complete waste of space. But if you’re the only kicker in the league who is worth anywhere near 2 wins, your returns will basically never be diminished. In basketball, roles and responsibilities aren’t nearly as wed to positions as they are in football, but the principle is the same. There is only one ball, and there are only so many responsibilities: If the source of one player’s value overlaps the source of another’s, they will both have less impact. Thus, if Rodman’s hypothetical I-Factor were real, one thing we might expect to find is a similar lack of diminishing returns—in other words, an unusual degree of consistency.
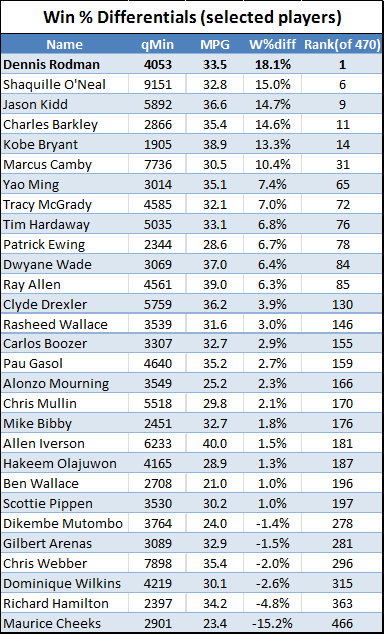
And indeed, Rodman’s impact was remarkably consistent. His adjusted win differential held at between 17% and 23% for 4 different teams, all of whom were championship contenders to one extent or another. Obviously the Bulls and Pistons each won multiple championships. The two years that Rodman spent with the pre-Tim-Duncan-era Spurs, they won 55 and 62 games respectively (the latter led the league that season, though the Spurs were eliminated by eventual-champion Houston in the Western Conference Finals). In 1999, Rodman spent roughly half of the strike-shortened season on the Lakers; in that time the Lakers went 17-6, matching San Antonio’s league-leading winning percentage. But, in a move that was somewhat controversial with the Lakers players at the time, Rodman was released before the playoffs began, and the Lakers fell in the 2nd round—to the eventual-champion Spurs.
But consistency should only be evidence of invisible value if it is unusual—that is, if it exists where we wouldn’t expect it to. So let’s look at Rodman’s consistency from a couple of different angles:
Angle 1: Money (again)
The following graph is similar to my ROI graph above, except instead of mapping the player’s salary to his win differential, I’m mapping the rest of the team’s salary to his win differential:
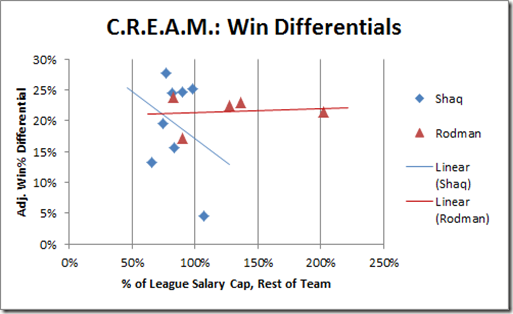
Note: Though obviously it’s only one data point and doesn’t mean anything, I find it amusing that the one time Shaq played for a team that had a full salary-cap’s worth of players without him, his win differential dropped to the floor.
So, basically, whether Rodman’s teams were broke or flush, his impact remained fairly constant. This is consistent with unusually low diminishing returns.
Angle 2: Position (again)
A potential objection I’ve actually heard a couple of times is that perhaps Rodman was able to have the impact he did because the circumstances he played in were particularly well-suited to never duplicating his skill-set: E.g., both Detroit and Chicago lacked dominant big men. Indeed, it’s plausible that part of his value came from providing the defense/rebounding of a dominant center, maximally leveraging his skill-set, and freeing up his teams to go with smaller, more versatile, and more offense-minded players at other positions (which could help explain why he had a greater impact on offensive efficiency than on defensive efficiency). However, all of this value would be visible. Moreover, the assumption that Rodman only played in these situations is false. Not only did Rodman play on very different teams with very different playing styles, he actually played on teams with every possible combination of featured players (or “1st and 2nd-best” players, if you prefer):
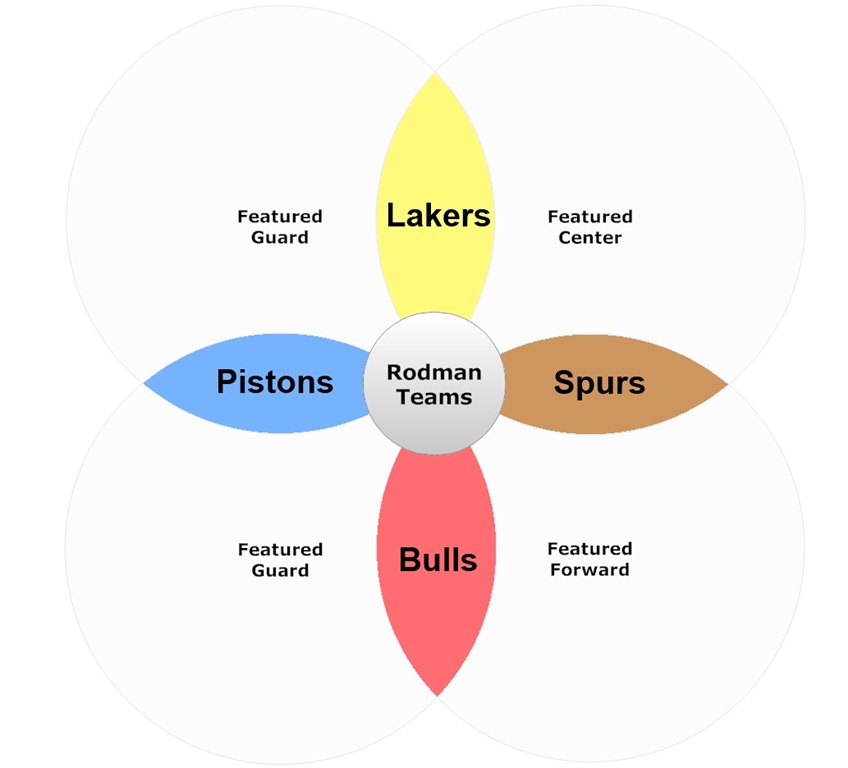
As we saw above, Rodman’s impact on all 4 teams was roughly the same. This too is consistent with an unusual lack of diminishing returns.
Evidence of Cause:
As I’ve said earlier, “role” can be very hard to define in the NBA relative to other sports. But to find meaningful evidence that Rodman provided an inordinate amount of value for his role, we don’t necessarily need to solve this intractable problem: we can instead look for “partial” or “imperfect” proxies. If some plausibly related proxy were to provide an unusual enough result, its actual relationship to the posited scenario could be self-reinforced—that is, the most likely explanation for the extremely unlikely result could be that it IS related to our hypothesis AND that our hypothesis is true.
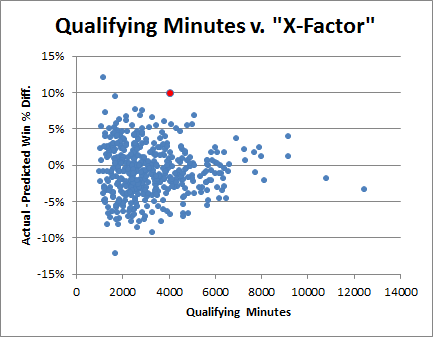
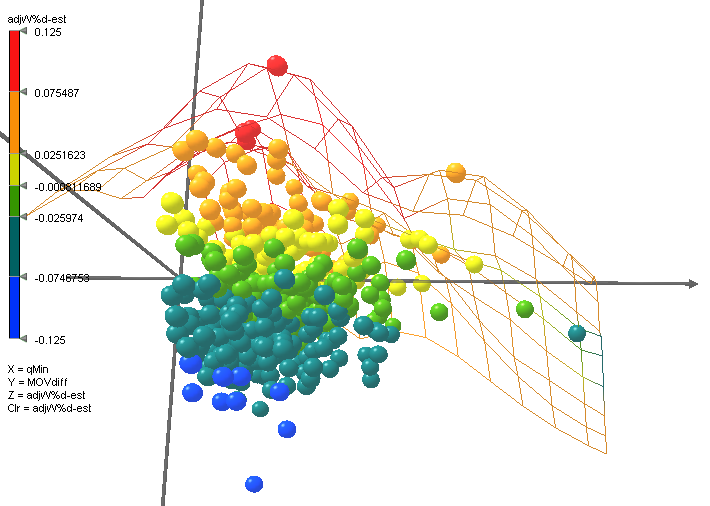
So one scarce resource that is plausibly related to role is “usage.” Usage Rate is the percentage of team possessions that a player “uses” by taking a shot or committing a turnover. Shooters obviously have higher usage rates than defender/rebounders, and usage generally has little correlation with impact. But let’s take a look at a scatter-plot of qualifying players from my initial differential study (limited to just those who have positive raw win differentials):
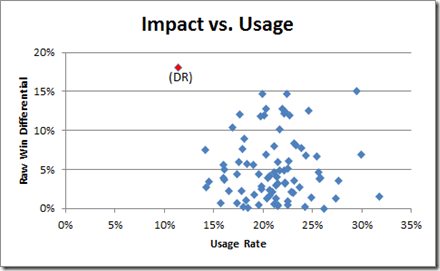
The red dot is obviously Dennis Rodman. Bonus points to anyone who said “Holy Crap” in their heads when they saw this graph: Rodman has both the highest win differential and the lowest Usage Rate, once again taking up residence in Outlier Land.
Let’s look at it another way: Treating possessions as the scarce resource, we might be interested in how much win differential we get for every possession that a player uses:
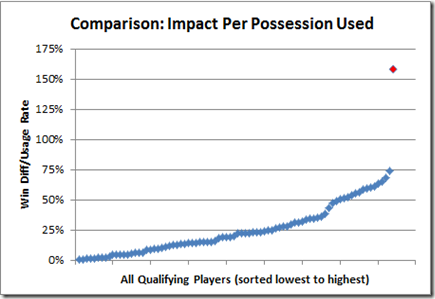
Let me say this in case any of you forgot to think it this time:
“Holy Crap!”
Yes, the red dot is Dennis Rodman. Oh, if you didn’t see it, don’t follow the blue line, it won’t help.
This chart isn’t doctored, manipulated, or tailored in any way to produce that result, and it includes all qualifying players with positive win differentials. If you’re interested, the Standard Deviation on the non-Rodman players in the pool is .19. Yes, that’s right, Dennis Rodman is nearly 4.5 standard deviations above the NEXT HIGHEST player. Hopefully, you see the picture of what could be going on here emerging: If value per possession is any kind of proxy (even an imperfect one) for value relative to role, it goes a long way toward explaining how Rodman was able to have such incredible impacts on so many teams with so many different characteristics.
The irony here is that the very aspect of Rodman’s game that frequently causes people to discount his value (“oh, he only does one thing”) may be exactly the quality that makes him a strong contender for first pick on the all-time NBA playground.
Conclusions:
Though the evidence is entirely circumstantial, I find the hypothesis very plausible, which in itself should be shocking. While I may not be ready to conclude that, yes, in fact, Rodman would actually be a more valuable asset to a potential championship contender than Michael freaking Jordan, I don’t think the opposite view is any stronger: That is, when you call that position crazy, conjectural, speculative, or naïve—as some of you inevitably will—I am fairly confident that, in light of the evidence, the default position is really no less so.
In fact, even if this hypothesis isn’t exactly true, I don’t think the next-most-likely explanation is that it’s completely false, and these outlandish outcomes were just some freakishly bizarre coincidence—it would be more likely that there is some alternate explanation that may be even more meaningful. Indeed, on some level, some of the freakish statistical results associated with Rodman are so extreme that it actually makes me doubt that the best explanation could actually stem from his athletic abilities. That is, he’s just a guy, how could he be so unusually good in such an unusual way? Maybe it actually IS more likely that the groupthink mentality of NBA coaches and execs accidentally DID leave a giant exploitable loophole in conventional NBA strategy; a loophole that Rodman fortuitously stumbled upon by having such a strong aversion to doing any of the things that he wasn’t the best at. If that is the case, however, the implications of this series could be even more severe than I intended.
Series Afterword:
Despite having spent time in law school, I’m not a lawyer. Indeed, one of the reasons I chose not to be one is because I get icky at the thought of picking sides first, and building arguments later.
In this case, I had strong intuitions about Rodman based on a variety of beliefs I had been developing about basketball value, combined with a number of seemingly-related statistical anomalies in Rodman’s record. Though I am naturally happy that my research has backed up those intuitions—even beyond my wildest expectations—I felt prepared for it to go the other way. But, of course, no matter how hard we try, we are all susceptible to bias.
Moreover, inevitably, certain non-material choices (style, structure, editorial, etc.) have to be made which emphasize the side of the argument that you are trying to defend. This too makes me slightly queasy, though I recognize it as a necessary evil in the discipline of rhetoric. My point is this: though I am definitely presenting a “case,” and it often appears one-sided, I have tried to conduct my research as neutrally as possible. If there is any area where you think I’ve failed in this regard, please don’t hesitate to let me know. I am willing to correct myself, beef up my research, or present compelling opposing arguments alongside my own; and though I’ve published this series in blog form, I consider this Case to be an ongoing project.
If you have any other questions, suggestions, or concerns, please bring them up in the comments (preferably) or email me and I will do my best to address them.
Finally, I would like to thank Nate Meyvis, Leo Wolpert, Brandon Wall, James Stuart, Dana Powers, and Aaron Nathan for the invaluable help they provided me by analyzing, criticizing, and/or ridiculing my ideas throughout this process. I’d also like to thank Jeff Bennett for putting me on this path, Scott Carder for helping me stay sane, and of course my wife Emilia for her constant encouragement.