This is part 2 of my “recap” of the Sloan Sports Analytics Conference that I attended in March (part 1 is here), mostly covering Day 2 of the event, but also featuring my petty way-too-long rant about Bill James (which I’ve moved to the end).
Day Two
First I attended the Football Analytics despite finding it disappointing last year, and, alas, it wasn’t any better. Eric Mangini must be the only former NFL coach willing to attend, b/c they keep bringing him back:
Just sat down for Football Analytics and I’m already bleh. In some ways, Mangini is worse than Brian Burke, b/c he acts like he cares. #SSAC
— Benjamin Morris (@skepticalsports) March 3, 2012
Overall, I spent more time in day 2 going to niche panels, research paper presentations and talking to people.
The last, in particular, was great. For example, I had a fun conversation with Henry Abbott about Kobe Bryant’s lack of “clutch.” This is one of Abbott’s pet issues, and I admit he makes a good case, particularly that the Lakers are net losers in “clutch” situations (yes, relative to other teams), even over the periods where they have been dominant otherwise.
Kobe is kind of a pivotal case in analytics, I think. First, I’m a big believer in “Count the Rings, Son” analysis: That is, leading a team to multiple championships is really hard, and only really great players do it. I also think he stands at a kind of nexus, in that stats like PER give spray shooters like him an unfair advantage, but more finely tuned advanced metrics probably over-punish the same. Part of the burden of Kobe’s role is that he has to take a lot of bad shots—the relevant question is how good he is at his job.
Abbott also mentioned that he liked one of my tweets, but didn’t know if he could retweet the non-family-friendly “WTF”:
Looking over the agenda, I don’t see “American Idol Analytics” anywhere. WTF? Competitive Singing is America’s 2nd favorite sport!#SSAC
— Benjamin Morris (@skepticalsports) March 2, 2012
I also had a fun conversation with Neil Paine of Basketball Reference. He seemed like a very smart guy, but this may be attributable to the fact that we seemed to be on the same page about so many things. Additionally, we discussed a very fun hypo: How far back in time would you have to go for the Charlotte Bobcats to be the odds-on favorites to win the NBA Championship?
As for the “sideshow” panels, they’re generally more fruitful and interesting than the ESPN-moderated super-panels, but they offer fewer easy targets for easy blog-griping. If you’re really interested in what went down, there is a ton of info at the SSAC website. The agenda can be found here. Information on the speakers is here. And, most importantly, videos of the various panels can be found here.
Box Score Rebooted
Featuring Dean Oliver, Bill James, and others.
This was a somewhat interesting, though I think slightly off-target, panel. They spent a lot of time talking about new data and metrics and pooh-poohing things like RBI (and even OPS), and the brave new world of play-by-play and video tracking, etc. But too much of this was discussing a different granularity of data than what can be improved in the current granularity levels. Or, in other words:
Solving box score problems w/ PBP or video data is fundamentally not “rebooting the box score.” What should be in box score but isn’t? #ssac
— Benjamin Morris (@skepticalsports) March 3, 2012
James acquitted himself a bit on this subject, arguing that boatloads of new data isn’t useful if it isn’t boiled down into useful metrics. But a more general way of looking at this is: If we were starting over from scratch, with a box-score-sized space to report a statistical game summary, and a similar degree of game-scoring resources, what kinds of things would we want to include (or not) that are different from what we have now? I can think of a few:
- In basketball, it’s archaic that free-throws aren’t broken down into bonus free throws and shot-replacing free throws.
- In football, I’d like to see passing stats by down and distance, or at least in a few key categories like 3rd and long.
- In baseball, I’d like to see “runs relative to par” for pitchers (though this can be computed easily enough from existing box scores).
In this panel, Dean Oliver took the opportunity to plug ESPN’s bizarre proprietary Total Quarterback Rating. They actually had another panel devoted just to this topic, but I didn’t go, so I’ll put a couple of thoughts here.
First, I don’t understand why ESPN is pushing this as a proprietary stat. Sure, no-one knows how to calculate regular old-fashioned quarterback ratings, but there’s a certain comfort in at least knowing it’s a real thing. It’s a bit like Terms of Service agreements, which people regularly sign without reading: at least you know the terms are out there, so someone actually cares enough to read them, and presumably they would raise a stink if you had to sign away your soul.
As for what we do know, I may write more on this come football season, but I have a couple of problems:
One, I hate the “clutch effect.” TQBR makes a special adjustment to value clutch performance even more than its generic contribution to winning. If anything, clutch situations in football are so bizarre that they should count less. In fact, when I’ve done NFL analysis, I’ve often just cut the 4th quarter entirely, and I’ve found I get better results. That may sound crazy, but it’s a bit like how some very advanced Soccer analysts have cut goal-scoring from their models, instead just focusing on how well a player advances the ball toward his goal: even if the former matters more, its unreliability may make it less useful.
Dean Oliver: You can criticize QBR, but nothing better to replace it. Hm. Try QBR minus the distorting clutch adjustment. #SSAC
— Benjamin Morris (@skepticalsports) March 3, 2012
Two, I’m disappointed in the way they “assign credit” for play outcomes:
Division of credit is the next step. Dividing credit among teammates is one of the most difficult but important aspects of sports. Teammates rely upon each other and, as the cliché goes, a team might not be the sum of its parts. By dividing credit, we are forcing the parts to sum up to the team, understanding the limitations but knowing that it is the best way statistically for the rating.
I’m personally very interested in this topic (and have discussed it with various ESPN analytics guys since long before TQBR was released). This is basically an attempt to address the entanglement problem that permeates football statistics. ESPN’s published explanation is pretty cryptic, and it didn’t seem clear to me whether they were profiling individual players and situations or had created credit-distribution algorithms league-wide.
At the conference, I had a chance to talk with their analytics guy who designed this part of the metric (his name escapes me), and I confirmed that they modeled credit distribution for the entire league and are applying it in a blanket way. Technically, I guess this is a step in the right direction, but it’s purely a reduction of noise and doesn’t address the real issue. What I’d really like to see is like a recursive model that imputes how much credit various players deserve broadly, then uses those numbers to re-assign credit for particular outcomes (rinse and repeat).
Deconstructing the Rebound With Optical Tracking Data
Rajiv Maheswaran, and other nerds.
This presentation was so awesome that I offered them a hedge bet for the “Best Research Paper” award. That is, I would bet on them at even money, so that if they lost, at least they would receive a consolation prize. They declined. And won. Their findings are too numerous and interesting to list, so you should really check it out for yourself.
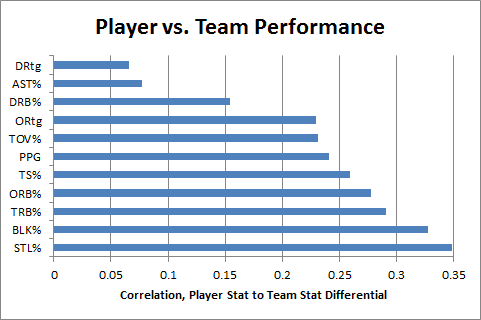
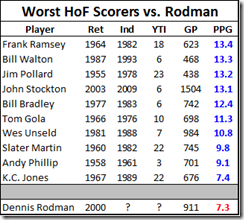
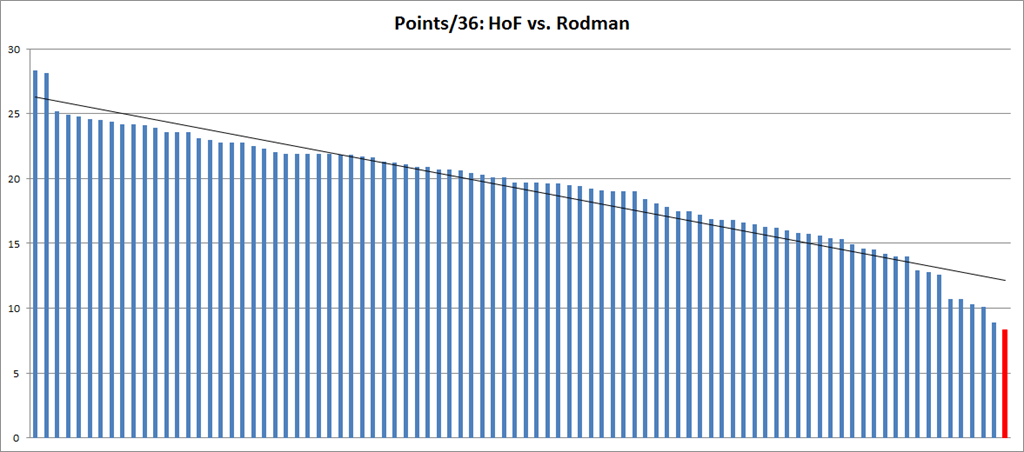
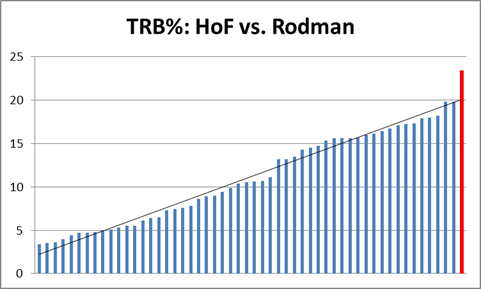
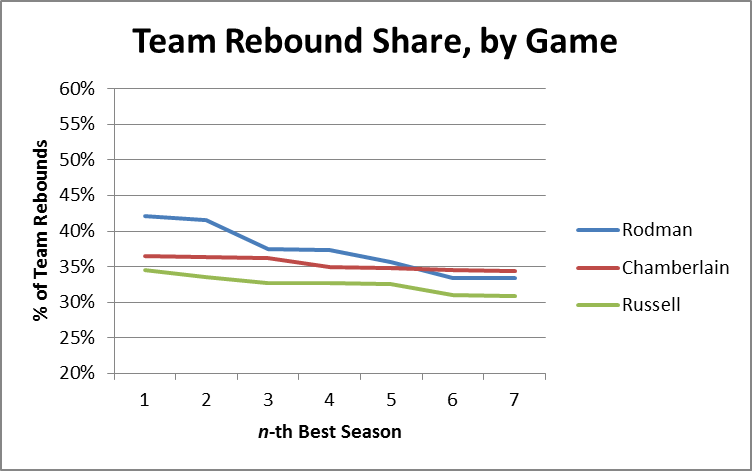
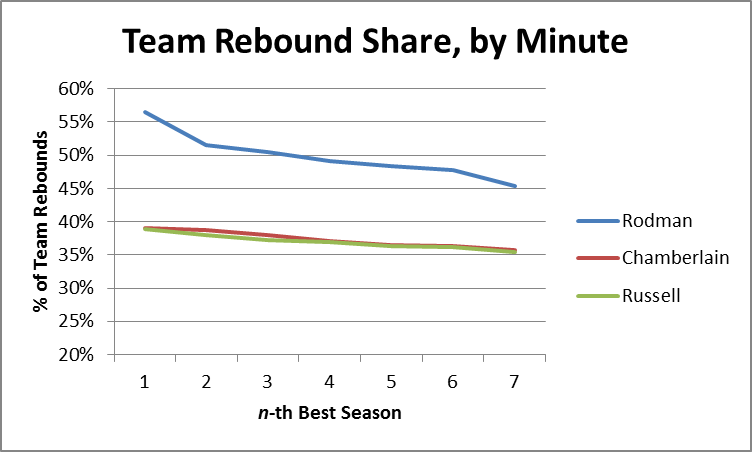
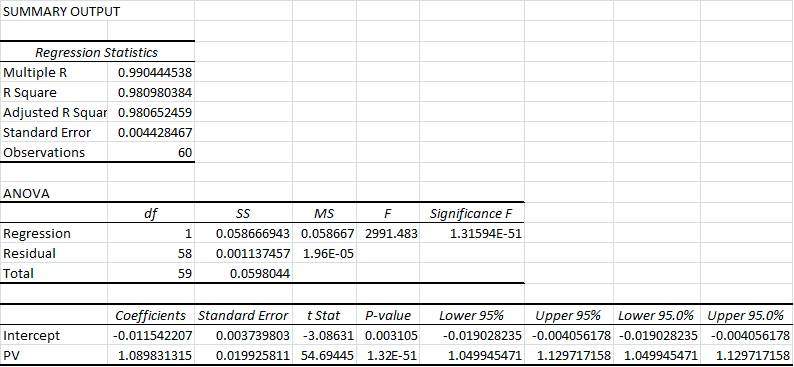
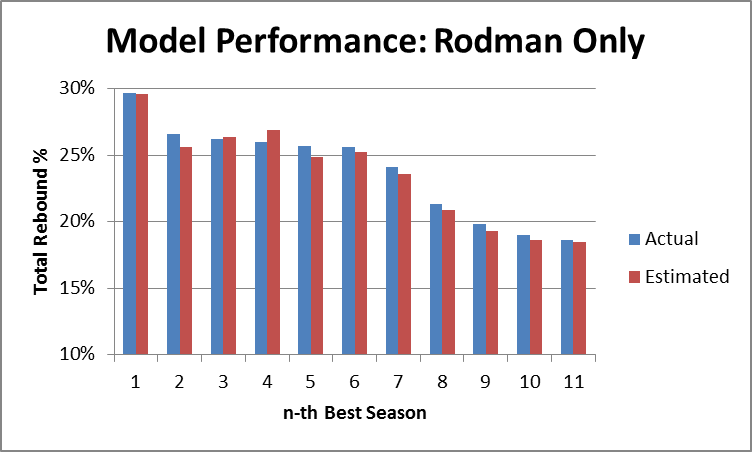
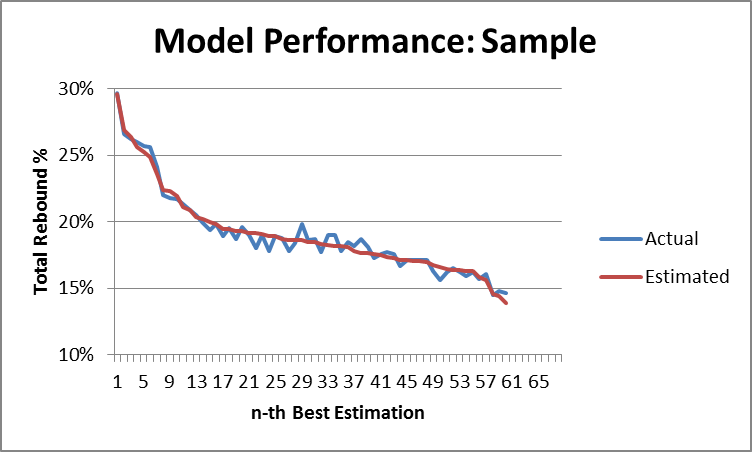
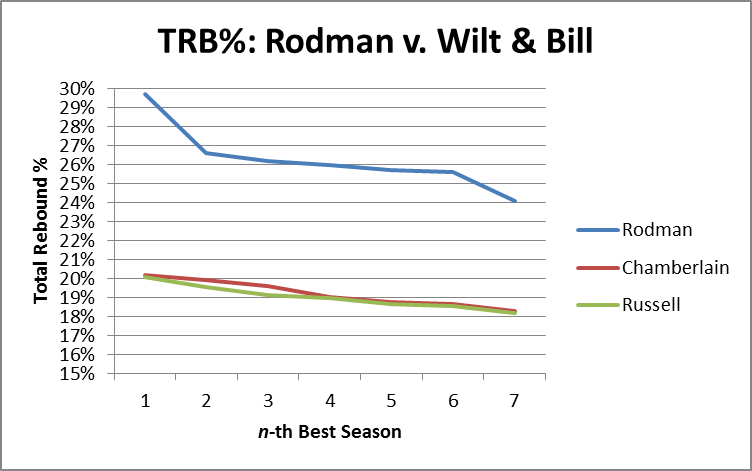
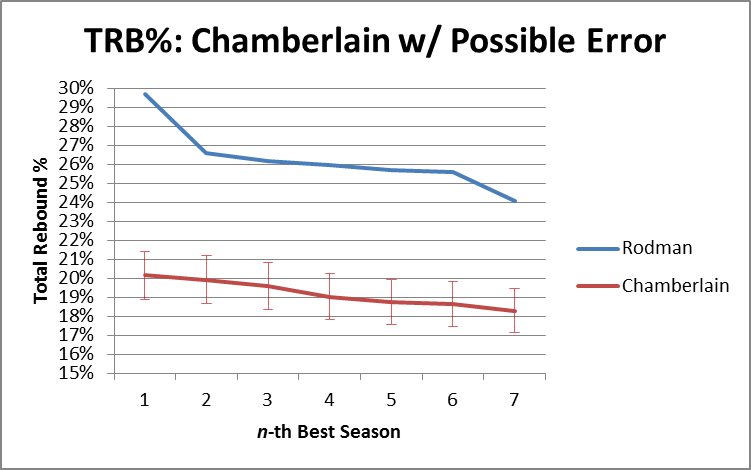
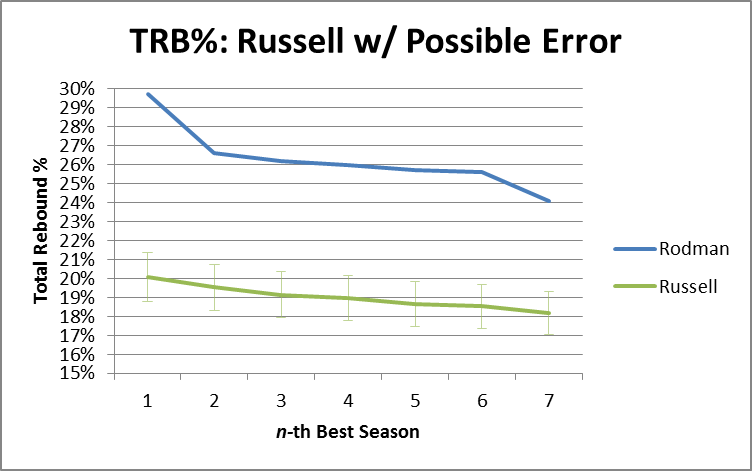
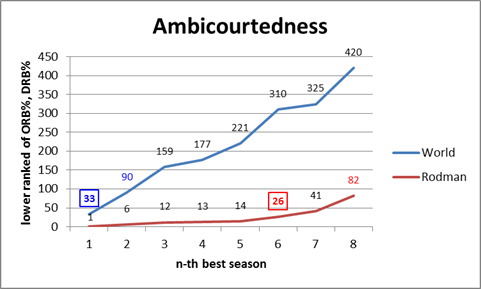
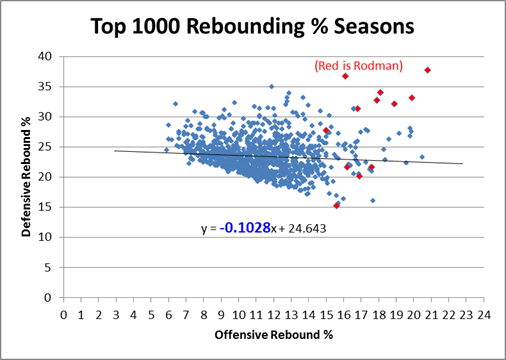
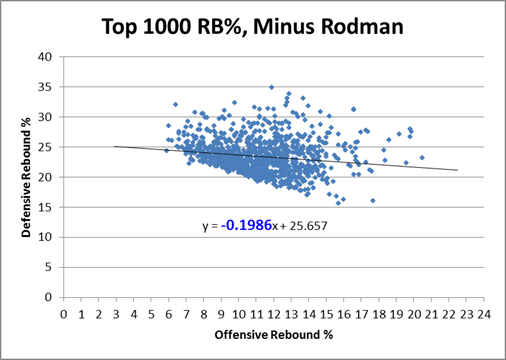
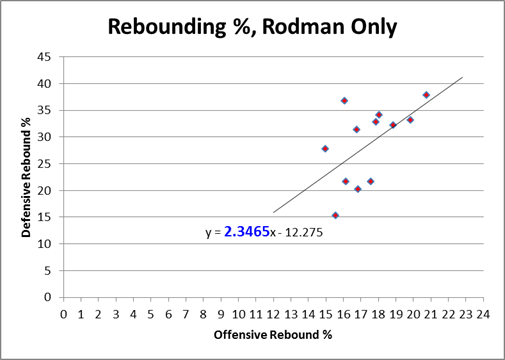
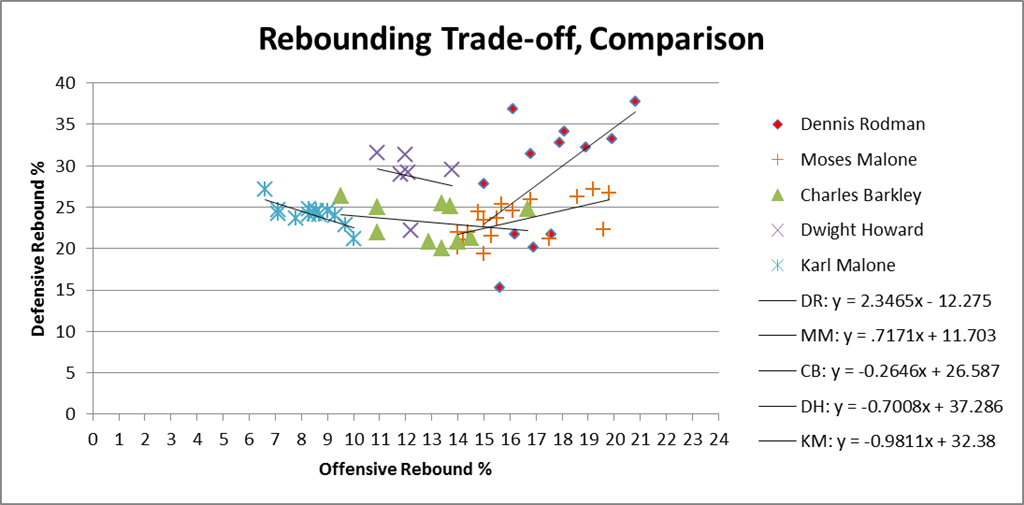
Obviously my work on the Dennis Rodman mystery makes me particularly interested in their theories of why certain players get more rebounds than others, as I tweeted in this insta-hypothesis:
So, upshot: Dennis Rodman’s incredible value could have come from him simply stepping into open spaces rather than following the ball. #SSAC
— Benjamin Morris (@skepticalsports) March 3, 2012
Following the presentation, I got the chance to talk with Rajiv for quite a while, which was amazing. Obviously they don’t have any data on Dennis Rodman directly, but Rajiv was also interested in him and had watched a lot of Rodman video. Though anecdotal, he did say that his observations somewhat confirmed the theory that a big part of Rodman’s rebounding advantage seemed to come from handling space very well:
- Even when away from the basket, Rodman typically moved to the open space immediately following a shot. This is a bit different from how people often think about rebounding as aggressively attacking the ball (or as being able to near-psychically predict where the ball is going to come down.
- Also rather than simply attacking the board directly, Rodman’s first inclination was to insert himself between the nearest opponent and the basket. In theory, this might slightly decrease the chances of getting the ball when it heads in toward his previous position, but would make up for it by dramatically increasing his chances of getting the ball when it went toward the other guy.
- Though a little less purely strategical, Rajiv also thought that Rodman was just incredibly good at #2. That is, he was just exceptionally good at jockeying for position.
To some extent, I guess this is just rebounding fundamentals, but I still think it’s very interesting to think about the indirect probabilistic side of the rebounding game.
Live B.S. Report with Bill James
Quick tangent: At one point, I thought Neil Paine summed me up pretty well as a “contrarian to the contrarians.” Of course, I’m don’t think I’m contrary for the sake of contrariness, or that I’m a negative person (I don’t know how many times I’ve explained to my wife that just because I hated a movie doesn’t mean I didn’t enjoy it!), it’s just that my mind is naturally inclined toward considering the limitations of whatever is put in front of it. Sometimes that means criticizing the status quo, and sometimes that means criticizing its critics.
So, with that in mind, I thought Bill James’s showing at the conference was pretty disappointing, particularly his interview with Bill Simmons.
I have a lot of respect for James. I read his Historical Baseball Abstract and enjoyed it considerably more than Moneyball. He has a very intuitive and logical mind. He doesn’t say a bunch of shit that’s not true, and he sees beyond the obvious. In Saturday’s “Rebooting the Box-score” panel, he made an observation that having 3 of 5 people on the panel named John implied that the panel was [likely] older than the rest of the room. This got a nice laugh from the attendees, but I don’t think he was kidding. And whether he was or not, he still gets 10 kudos from me for making the closest thing to a Bayesian argument I heard all weekend. And I dutifully snuck in for a pic with him:
James was somewhat ahead of his time, and perhaps he’s still one of the better sports analytic minds out there, but in this interview we didn’t really get to hear him analyze anything, you know, sportsy. This interview was all about Bill James and his bio and how awesome he was and how great he is and how hard it was for him to get recognized and how much he has changed the game and how, without him, the world would be a cold, dark place where ignorance reigned and nobody had ever heard of “win maximization.”
Bill Simmons going this route in a podcast interview doesn’t surprise me: his audience is obviously much broader than the geeks in the room, and Simmons knows his audience’s expectations better than anyone. What got to me was James’s willingness to play along, and everyone else’s willingness to eat it up. Here’s an example of both, from the conference’s official Twitter account:
Quote of the day RT @SloanSportsConf: “this conference is a culmination of 30 years of my work” — Bill James #SSAC
— MIT Sports Conf. (@SloanSportsConf) March 3, 2012
Perhaps it’s because I never really liked baseball, and I didn’t really know anyone did any of this stuff until recently, but I’m pretty certain that Bill James had virtually zero impact on my own development as a sports data-cruncher. When I made my first PRABS-style basketball formula in the early 1990’s (which was absolutely terrible, but is still more predictive than PER), I had no idea that any sports stats other than the box score even existed. By the time I first heard the word “sabermetrics,” I was deep into my own research, and didn’t bother really looking into it deeply until maybe a few months ago.
Which is not to say I had no guidance or inspiration. For me, a big epiphanous turning point in my approach to the analysis of games did take place—after I read David Sklansky’s Theory of Poker. While ToP itself was published in 1994, Sklansky’s similar offerings date back to the 70s, so I don’t think any broader causal pictures are possible.
More broadly, I think the claim that sports analytics wouldn’t have developed without Bill James is preposterous. Especially if, as i assume we do, we firmly believe we’re right. This isn’t like L. Ron Hubbard and Incident II: being for sports analytics isn’t like having faith in a person or his religion. It simply means trying to think more rigorously about sports, and using all of the available analytical techniques we can to gain an advantage. Eventually, those who embrace the right will win out, as we’ve seen begin to happen in sports, and as has already happened in nearly every other discipline.
Indeed, by his own admission, James liked to stir controversy, piss people off, and talk down to the old guard whenever possible. As far as we know, he may have set the cause of sports analytics back, either by alienating the people who could have helped it gain acceptance, or by setting an arrogant and confrontational tone for his disciples (e.g., the uplifting “don’t feel the need to explain yourself” message in Moneyball). I’m not saying that this is the case or even a likely possibility, I’m just trying to illustrate that giving someone credit for all that follows—even a pioneer like James—is a dicey game that I’d rather not participate in, and that he definitely shouldn’t.
On a more technical note, one of his oft-quoted and re-tweeted pearls of wisdom goes as follows:
Bill James on whether we’ve exhausted all baseball advanced stats: “We’ve only taken a bucket of knowledge from a sea of ignorance.” #ssac
— Gill Alexander (@beatingthebook) March 2, 2012
Sounds great, right? I mean, not really, I don’t get the metaphor: if the sea is full of ignorance, why are you collecting water from it with a bucket rather than some kind of filtration system? But more importantly, his argument in defense of this claim is amazingly weak. When Simmons asked what kinds of things he’s talking about, he repeatedly emphasized that we have no idea whether a college sophomore will turn out to be a great Major League pitcher. True, but, um, we never will. There are too many variables, the input and outputs are too far apart in time, and the contexts are too different. This isn’t the sea of ignorance, it’s a sea of unknowns.
Which gets at one of my big complaints about stats-types generally. A lot of people seem to think that stats are all about making exciting discoveries and answering questions that were previously unanswerable. Yes, sometimes you get lucky and uncover some relationship that leads to a killer new strategy or to some game-altering new dynamic. But most of the time, you’ll find static. A good statistical thinker doesn’t try to reject the static, but tries to understand it: Figuring out what you can’t know is just as important as figuring out what you can know.
On Twitter I used this analogy:
I also don’t know whether this coin will come up heads or tails, but that doesn’t mean I have a poor understanding of coin-flipping. #SSAC
— Benjamin Morris (@skepticalsports) March 2, 2012
Success comes with knowing more true things and fewer false things than the other guy.