The Case for Dennis Rodman, Part 4/4(b): The Finale (Or, “Rodman v. Jordan 2”)

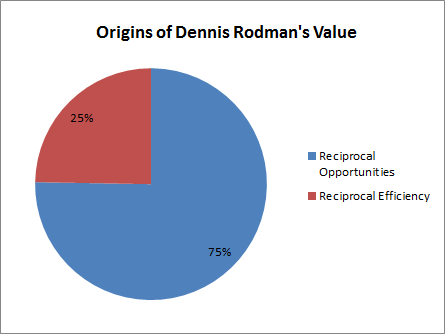
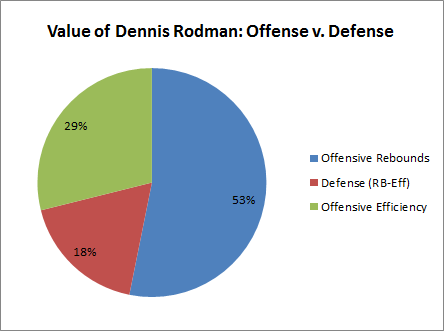
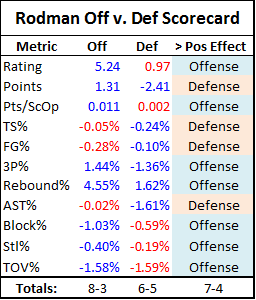
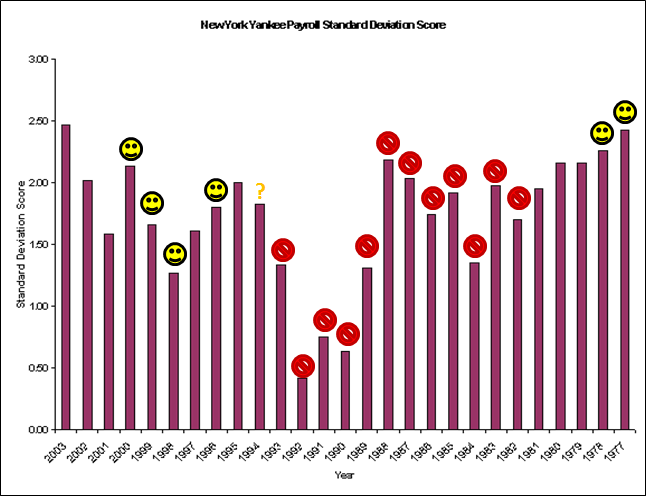
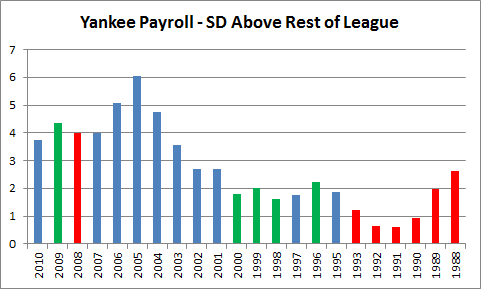
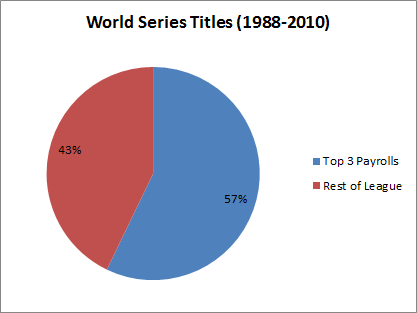
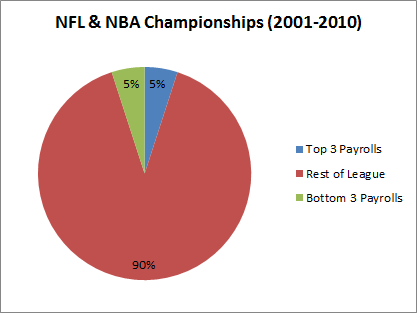
[ADDED: Unsurpisingly, this post has been getting a lot of traffic, which I assume includes a number of new readers who are unfamiliar with my “Case For Dennis Rodman.” So, for the uninitiated, I’d like to (at least temporarily) repeat a few of my late-comer intro points from Part 4(a): “The main things you need to know about this series are that it’s 1) extremely long (sprawling over 13 sections in 4 parts), 2) ridiculously (almost comically) detailed, and 3) only partly about Dennis Rodman. There is a lot going on, so to help new and old readers alike, I have a newly-updated “Rodman Series Guide,” which includes a broken down list of articles, a sampling of some of the most important graphs and visuals, and a giant table summarizing the entire series by post, including the main points on both sides of the analysis.”]

So it comes down to this: With Rodman securely in the Hall of Fame, and his positive impact conclusively demonstrated by the most skeptical standards of proof I can muster, what more is there to say? Repeatedly, my research on Rodman has led to unexpectedly extreme discoveries: Rodman was not just a great rebounder, but the greatest of all time—bar none. And despite playing mostly for championship contenders, his differential impact on winning was still the greatest measured of any player with data even remotely as reliable as his. The least generous interpretation of the evidence still places Rodman’s value well within the realm of the league’s elite, and in Part 4(a) I explored some compelling reasons why the more generous interpretation may be the most plausible.

Yet even that more generous position has its limitations. Though the pool of players I compared with Rodman was broadly representative of the NBA talent pool on the whole, it lacked a few of the all-time greats—in particular, the consensus greatest: Michael Jordan. Due to that conspicuous absence, as well as to the considerable uncertainty of a process that is better suited to proving broad value than providing precise individual ratings, I have repeatedly reminded my readers that, even though Rodman kept topping these lists and metrics, I did NOT mean to suggest that Rodman was actually greater than the greatest of them all. In this final post of this series, I will consider the opposite position: that there is a plausible argument (with evidence to back it up) that Rodman’s astounding win differentials—even taken completely at face value—may still understate his true value by a potentially game-changing margin.

A Dialogue:

First off, this argument was supposed to be an afterthought. Just a week ago—when I thought I could have it out the next morning—it was a few paragraphs of amusing speculation. But, as often seems to be the case with Dennis Rodman-related research, my digging uncovered a bit more than I expected.

The main idea has its roots in a conversation I had (over bruschetta) with a friend last summer. This friend is not a huge sports fan, nor even a huge stats geek, but he has an extremely sharp analytical mind, and loves, loves to tear apart arguments—and I mean that literally: He has a Ph.D. in Rhetoric. In law school, he was the guy who annoyed everyone by challenging almost everything the profs ever said—and though I wouldn’t say he was usually right, I would say he was usually onto something.

That night, I was explaining my then-brand new “Case for Dennis Rodman” project, which he was naturally delighted to dissect and criticize. After painstakingly laying out most of The Case—of course having to defend and explain many propositions that I had been taking for granted and needing to come up with new examples and explanations on the fly, just to avoid sounding like an idiot (seriously, talking to this guy can be intense)—I decided to try out this rhetorical flourish that made a lot of sense to me intuitively, but which had never really worked for anyone previously:

“Let me put it this way: Rodman was by far the best third-best player in NBA History.”

As I explained, “third best” in this case is sort of a term of art, not referring to quality, but to a player’s role on his team. I.e., not the player a team is built around (1st best), or even the supporting player in a “dynamic duo” (like HOF 2nd-besters Scotty Pippen or John Stockton), but the guy who does the dirty work, who mostly gets mentioned in contexts like, “Oh yeah, who else was on that [championship] team? Oh that’s right, Dennis Rodman”).

“Ah, so how valuable is the best third-best player?”

At the time, I hadn’t completely worked out all of the win percentage differentials and other fancy stats that I would later on, but I had done enough to have a decent sense of it:

“Well, it’s tough to say when it’s hard to even define ‘third-best’ player, but [blah blah, ramble ramble, inarticulate nonsense] I guess I’d say he easily had 1st-best player value, which [blah blah, something about diminishing returns, blah blah] . . . which makes him the best 3rd-best player by a wide margin”.

“How wide?”

“Well, it’s not like he’s as valuable as Michael Jordan, but he’s the best 3rd-best player by a wider margin than Jordan was the best 1st-best player.”

“So you’re saying he was better than Michael Jordan.”

“No, I’m not saying that. Michael Jordan was clearly better.”

“OK, take a team with Michael Jordan and Dennis Rodman on it. Which would hurt them more, replacing Michael Jordan with the next-best primary scoring option in NBA history, or replacing Rodman with the next-best defender/rebounder in NBA history?”

“I’m not sure, but probably Rodman.”

“So you’re saying a team should dump Michael Jordan before it should dump Dennis Rodman?”

“Well, I don’t know for sure, I’m not sure exactly how valuable other defender-rebounders are, but regardless, it would be weird to base the whole argument on who happens to be the 2nd-best player. I mean, what if there were two Michael Jordan’s, would that make him the least valuable starter on an All-Time team?”

“Well OK, how common are primary scoring options that are in Jordan’s league value-wise?”

“There are none, I’m pretty sure he has the most value.”

“BALLPARK.”

“I dunno, there are probably between 0 and 2 in the league at any given time.”

“And how common are defender/rebounder/dirty workers that are in Rodman’s league value-wise?”

“There are none.”

“BALLPARK.”

“There are none. Ballpark.”

“So, basically, if a team had Michael Jordan and Dennis Rodman on it, and they could replace either with some random player ‘in the ballpark’ of the next-best player for their role, they should dump Jordan before they dump Rodman?”

“Maybe. Um. Yeah, probably.”

“And I assume that this holds for anyone other than Jordan?”

“I guess.”

“So say you’re head-to-head with me and we’re drafting NBA All-Time teams, you win the toss, you have first pick, who do you take?”

“I don’t know, good question.”

“No, it’s an easy question. The answer is: YOU TAKE RODMAN. You just said so.”

“Wait, I didn’t say that.”

“O.K., fine, I get the first pick. I’ll take Rodman. . . Because YOU JUST TOLD ME TO.”

“I don’t know, I’d have to think about it. It’s possible.”

Up to this point, I confess, I’ve had to reconstruct the conversation to some extent, but these last two lines are about as close to verbatim as my memory ever gets:

“So there you go, Dennis Rodman is the single most valuable player in NBA History. There’s your argument.”

“Dude, I’m not going to make that argument. I’d be crucified. Maybe, like, in the last post. When anyone still reading has already made up their mind about me.”

And that’s it. Simple enough, at first, but I’ve thought about this question a lot between last summer and last night, and it still confounds me: Could being the best “3rd-best” player in NBA history actually make Rodman the best player in NBA history? For starters, what does “3rd-best” even mean? The argument is a semantic nightmare in its own right, and an even worse nightmare to formalize well enough to investigate. So before going there, let’s take a step back:

The Case Against Dennis Rodman:

At the time of that conversation, I hadn’t yet done my league-wide study of differential statistics, so I didn’t know that Rodman would end up having the highest I could find. In fact, I pretty much assumed (as common sense would dictate) that most star-caliber #1 players with a sufficient sample size would rank higher: after all, they have a greater number of responsibilities, they handle the ball more often, and should thus have many more opportunities for their reciprocal advantage over other players to accumulate. Similarly, if a featured player can’t play—potentially the centerpiece of his team, with an entire offense designed around him and a roster built to supplement him—you would think it would leave a gaping hole (at least in the short-run) that would be reflected heavily in his differentials. Thus, I assumed that Rodman probably wouldn’t even “stat out” as the best Power Forward in the field, making this argument even harder to sell. But as the results revealed, it turns out feature players are replaceable after all, and Rodman does just fine on his own. However, there are a couple of caveats to this outcome:

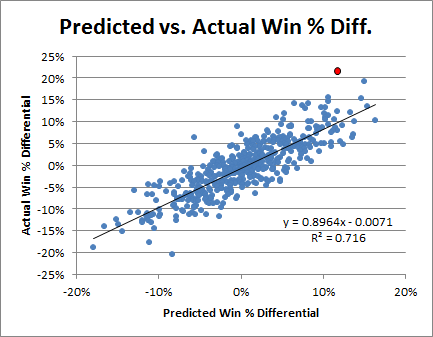
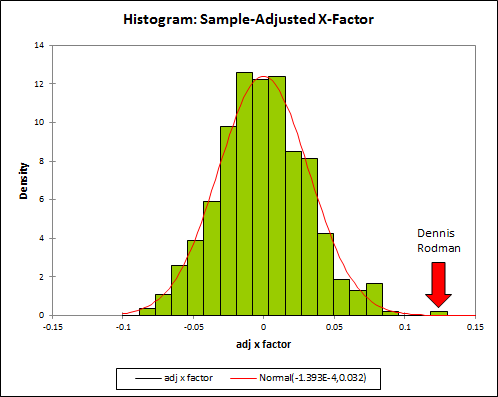
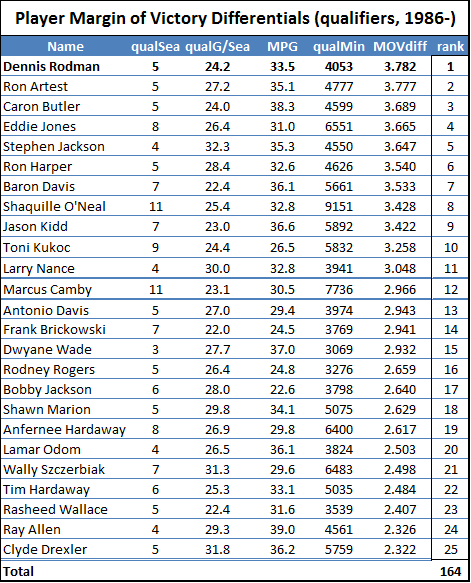
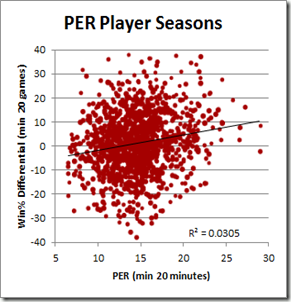
First, without much larger sample sizes, I wouldn’t say that game-by-game win differentials are precise enough to settle disputes between players of similar value. For example, the standard deviation for Rodman’s 22% adjusted win differential is still 5% (putting him less than a full standard deviation above some of the competition). This is fine for concluding that he was extremely valuable, but it certainly isn’t extreme enough to outright prove the seemingly farfetched proposition that he was actually the most valuable player overall. The more unlikely you believe that proposition to be, the less you should find this evidence compelling—this is a completely rational application of Bayes’ Theorem—and I’m sure most of you, ex ante, find the proposition very very unlikely. Thus, to make any kind of argument for Rodman’s superiority that anyone but the biggest Rodman devotees would find compelling, we clearly need more than win differentials.

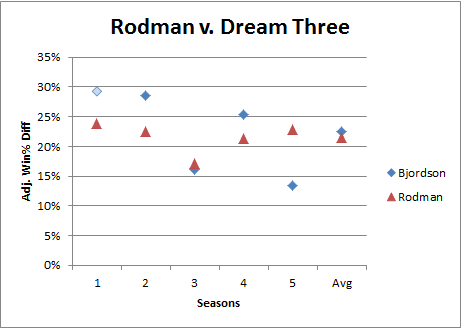
Second, it really is a shame that a number of the very best players didn’t qualify for the study—particularly the ultimate Big Three: Michael Jordan, Magic Johnson, and Larry Bird (who, in maybe my favorite stat ever, never had a losing month in his entire career). As these three are generally considered to be in a league of their own, I got the idea: if we treated them as one player, would their combined sample be big enough to make an adequate comparison? Well, I had to make a slight exception to my standard filters to allow Magic Johnson’s 1987 season into the mix, but here are the results:

Adjusted Win percentage differential is Rodman’s most dominant value stat, and here, finally, Herr Bjordson edges him. Plus this may not fully represent these players’ true strength: the two qualifying Jordan seasons are from his abrupt return in 1994 and his first year with the Wizards in 2001, and both of Bird’s qualifying seasons are from the last two of his career, when his play may have been hampered by a chronic back injury. Of course, just about any more-conventional player valuation system would rank these players above (or way above) Rodman, and even my own proprietary direct “all-in-one” metric puts these three in their own tier with a reasonable amount of daylight between them and the next pack (which includes Rodman) below. So despite having a stronger starting position in this race than I would have originally imagined, I think it’s fair to say that Rodman is still starting with a considerable disadvantage.

Trade-offs and Invisible Value:

So let’s assume that at least a few players offer more direct value than Dennis Rodman. But building a Champion involves more than putting together a bunch of valuable players: to maximize your chances of success, you must efficiently allocate a variety of scare resources, to obtain as much realized value as possible, through a massively complicated set of internal and external constraints.

For example, league rules may affect how much money you can spend and how many players you can carry on your roster. Game rules dictate that you only have so many players on the floor at any given time, and thus only have so many minutes to distribute. Strategic realities require that certain roles and responsibilities be filled: normally, this means you must have a balance of talented players who play different positions—but more broadly, if you hope to be successful, your team must have the ability to score, to defend, to rebound, to run set plays, to make smart tactical maneuvers, and to do whatever else that goes into winning. All of these little things that your team has to do can also be thought of as a limited resource: in the course of a game, you have a certain number of things to be done, such as taking shots, going after loose balls, setting up a screens, contesting rebounds, etc. Maybe there are 500 of these things, maybe 1000, who knows, but there are only so many to go around—and just as with any other scarce resource, the better teams will be the ones that squeeze the most value out of each opportunity.

Obviously, some players are better at some things than others, and may contribute more in some areas than others—but there will always be trade-offs. No matter how good you are, you will always occupy a slot on the roster and a spot on the floor, every shot you take or every rebound you get means that someone else can’t take that shot or get that rebound, and every dollar your team spends on you is a dollar they can’t spend on someone else. Thus, there are two sides to a player’s contribution: how much surplus value he provides, and how much of his team’s scarce resources he consumes.

The key is this: While most of the direct value a player provides is observable, either directly (through box scores, efficiency ratings, etc.) or indirectly (Adjusted +/-, Win Differentials), many of his costs are concealed.

Visible v. Invisible Effects

Two players may provide seemingly identical value, but at different costs. In very limited contexts this can be extremely clear: thought it took a while to catch on, by now all basketball analysts realize that scoring 25 points per game on 20 shots is better than scoring 30 points a game on 40 shots. But in broader contexts, it can be much trickier. For example, with a large enough sample size, Win Differentials should catch almost anything: everything good that a player does will increase his team’s chances of winning when he’s on the floor, and everything bad that he does will decrease his team’s chances of losing when he’s not. Shooting efficiency, defense, average minutes played, psychological impact, hustle, toughness, intimidation—no matter how abstract the skill, it should still be reflected in the aggregate.

No matter how hard the particular skill (or weakness) is to identify or understand, if its consequences would eventually impact a player’s win differentials, (for these purposes) its effects are visible.

But there are other sources of value (or lack thereof) which won’t impact a player’s win differentials—these I will call “invisible.” Some are obvious, and some are more subtle:

Example 1: Money

“Return on Investment” is the prototypical example of invisible value, particularly in a salary-cap environment, where every dollar you spend on one player is a dollar you can’t spend on another. No matter how good a player is, if you give up more to get him than you get from him in return, your team suffers. Similarly, if you can sign a player for much less than he is worth, he may help your team more than other (or even better) players who would cost more money.

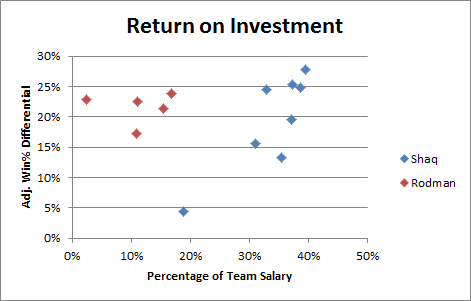
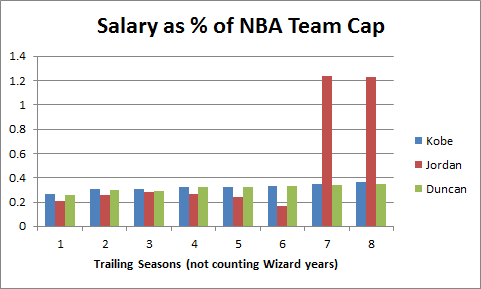
This value is generally “invisible” because the benefit that the player provides will only be realized when he plays, but the cost (in terms of limiting salary resources) will affect his team whether he is in the lineup or not. And Dennis Rodman was basically always underpaid (likely because the value of his unique skillset wasn’t fully appreciated at the time):

^{Note: For a fair comparison, this graph (and the similar one below) includes only the 8 qualifying Shaq seasons from before he began to decline.}

Aside from the obvious, there are actually a couple of interesting things going on in this graph that I’ll return to later. But I don’t really consider this a primary candidate for the “invisible value” that Rodman would need to jump ahead of Jordan, primarily for two reasons:

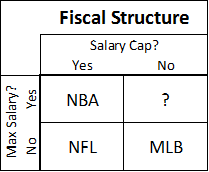
First, return on investment isn’t quite as important in the NBA as it is in some other sports: For example, in the NFL, with 1) so many players on each team, 2) a relatively hard salary cap (when it’s in place, anyway), and 3) no maximum player salaries, ROI is perhaps the single most important consideration for the vast majority of personnel decisions. For this reason, great NFL teams can be built on the backs of many underpaid good-but-not-great players (see my extended discussion of fiscal strategy in major sports here).

Second, as a subjective matter, when we judge a player’s quality, we don’t typically consider factors that are external to their actual athletic attributes. For example, a great NFL quarterback could objectively hurt his team if he is paid too much, but we still consider him great. When we ask “who’s the best point guard in the NBA,” we don’t say, “IDK, how much more does Chris Paul get paid than Jason Kidd?” Note this is basically a social preference: It’s conceivable that in some economically-obsessed culture, this sort of thing really would be the primary metric for player evaluation. But personally, and for the purposes of my argument, I prefer our more traditional values on this one.

Example 2: Position

In the “perfect timing” department, a commenter “Siddy Hall” recently raised a hypothetical very similar to my friend’s:

You get 8 people in a room, all posing as GM’s. We’re allowed to select 5 players each from the entire history of the NBA. Then we’ll have a tournament. At PF, I would grab Rodman. And I’m confident that I’d win because he’s on my team. He’d dominate the glass and harass and shutdown a superstar. I think he’s the finest PF to ever play the game.

Of course, you need to surround him with some scorers, but when is that ever a problem?

The commenter only explicitly goes so far as to say that Rodman would be the most valuable power forward. Yet he says he is “confident” that he would win, with the only caveat being that his team gets other scorers (which is a certainty). So, he thinks Rodman is the best PF by a wide enough margin that his team would be a favorite against the team that got Michael Jordan. Let me play the role of my friend above: whether he means to or not, he’s basically saying that Rodman is more valuable than Jordan.

In this example, “position” is the scarce resource. Just as a player can be valuable for the amount of money the team must spend on him, he can also be valuable for his position. But this value can be visible, invisible, or both.

This is probably easiest to illustrate in the NFL, where positions and responsibilities are extremely rigid. An example I used in response to the commenter is that an NFL kicker who could get you 2 extra wins per season could be incredibly valuable. These two extra wins obviously have visible value: By definition, this is a player for whom we would expect to observe a 2 game per season win differential. But there’s another, very important way in which this player’s value would be much greater. As I said in response to the commenter, a +2 kicker could even be more valuable than a +4 quarterback.

In order to play the 2 win kicker, the only cost is your kicker slot, which could probably only get you a fraction of a win even if you had one of the best in the league on your team (relevant background note: kickers normally don’t contribute much, particularly since bad kickers likely influence their teams to make better tactical decisions, and vice-versa). But to play a 4-win quarterback, the cost is your quarterback slot. While the average QB and the average kicker are both worth approximately 0 games, good quarterbacks are often worth much more, and good kickers are worth very little.

Put most simply, because there are no other +2 kickers, that kicker could get 2 wins for virtually ANY team. The +4 QB would only provide 2 wins for teams who would be unable to acquire a +2 quarterback by other means. Or you can think about it conversely: Team A signs the kicker, and Team B signs the QB. For the moment, Team B might appear better, but the most value they will ever be able to get out of their QB/Kicker tandem is +4 games plus epsilon. Team A, on the other hand, can get more value out of their QB/kicker combo than Team B simply by signing any QB worth +2 or greater, who are relatively common.

Why does this matter? Well, in professional sports, we care about one thing more than any other: championships. Teams that win championships do so by having the best roster with the most value. Players like our special kicker provide unique avenues to surplus value that even great other players can’t.

To generalize a bit, you could say that value vs. a replacement player is generally visible, as it will be represented in win differentials no matter who you play for. But a player’s value relative to the entire distribution of players at his position can lead to substantial invisible benefits, as it can substantially improve his team’s ability to build a championship contender.

Formalizing “I-Factor”

Unfortunately, in basketball, such distinctions are much more nebulous. Sure, there are “positions,” but the spot where you line up on the floor is very different from the role you play. E.g., your primary scoring responsibilities can come from any position. And even then “roles” are dynamic and loosely defined (if at all)—some roles that are crucial to certain teams don’t even exist on others. Plus, teams win in different ways: you can do it by having 5 options on offense with 5 guys that can do everything (OK, this doesn’t happen very often, but the Pistons did it in 03-04), or you can be highly specialized and try to exploit the comparative advantages between your players (this seems to be the more popular model of late).

Rodman was a specialist. He played on teams that, for the most part, didn’t ask him to do more than what he was best at—and that probably helped him fully leverage his talents. But the truly amazing part is how much of a consistent impact he could have, on such a variety of different teams, and with seemingly so few responsibilities.

So let’s posit a particular type of invisible value and call it “I-Factor,” with the following elements:

It improves your team’s chances of building a championship contender.
It wouldn’t be reflected in your game-to-game win differential.
It stems from some athletic or competitive skill or attribute.

In the dialogue above, I suggested that Rodman had an inordinate positive impact for a “3rd-best” player, and my friend suggested (insisted really) that this alone should vault him above great but more ordinary “1st-best” players, even if they had significantly more observable impact. Putting these two statements together, we have an examinable hypothesis: That Dennis Rodman’s value relative to his role constituted a very large “I-Factor.”

Evaluating the Hypothesis:

Because the value we’re looking for is (by definition) invisible, its existence is ridiculously hard—if not impossible—to prove empirically (which is why this argument is the dessert instead of the main course of this series).

However, there could be certain signs and indicators we can look for that would make the proposition more likely: specifically, things that would seem unusual or unlikely if the hypothesis were false, but which could be explainable either as causes or effects of the hypothesis being true.

Since the hypothesis posits both an effect (very large I-Factor), and a cause (unusually high value for his role), we should primarily be on the lookout for two things: 1) any interesting or unusual patterns that could be explainable as a consequence of Rodman having a large I-Factor, and 2) any interesting or unusual anomalies that could help indicate that Rodman had an excessive amount of value for his role.

Evidence of Effect:

To lighten the mood a bit, let’s start this section off with a riddle:

Q. What do you get for the team that has everything?

A. Dennis Rodman.

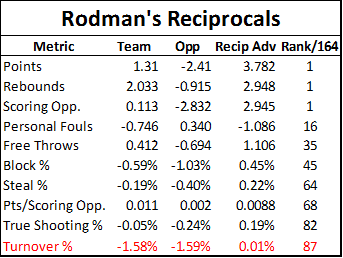
Our hypothetical Rodman I-Factor is much like that of our hypothetical super-kicker in the NFL example above. The reason that kicker was even more valuable than the 2 wins per season he could get you is that he could get those 2 wins for anyone. Normally, if you have a bunch of good players and you add more good players, the whole is less than the sum of its parts. In the sports analytics community, this is generally referred to as “diminishing returns.” An extremely simple example goes like this: Having a great quarterback on your team is great. Having a second great quarterback is maybe mildly convenient. Having a third great quarterback is a complete waste of space. But if you’re the only kicker in the league who is worth anywhere near 2 wins, your returns will basically never be diminished. In basketball, roles and responsibilities aren’t nearly as wed to positions as they are in football, but the principle is the same. There is only one ball, and there are only so many responsibilities: If the source of one player’s value overlaps the source of another’s, they will both have less impact. Thus, if Rodman’s hypothetical I-Factor were real, one thing we might expect to find is a similar lack of diminishing returns—in other words, an unusual degree of consistency.

And indeed, Rodman’s impact was remarkably consistent. His adjusted win differential held at between 17% and 23% for 4 different teams, all of whom were championship contenders to one extent or another. Obviously the Bulls and Pistons each won multiple championships. The two years that Rodman spent with the pre-Tim-Duncan-era Spurs, they won 55 and 62 games respectively (the latter led the league that season, though the Spurs were eliminated by eventual-champion Houston in the Western Conference Finals). In 1999, Rodman spent roughly half of the strike-shortened season on the Lakers; in that time the Lakers went 17-6, matching San Antonio’s league-leading winning percentage. But, in a move that was somewhat controversial with the Lakers players at the time, Rodman was released before the playoffs began, and the Lakers fell in the 2nd round—to the eventual-champion Spurs.

But consistency should only be evidence of invisible value if it is unusual—that is, if it exists where we wouldn’t expect it to. So let’s look at Rodman’s consistency from a couple of different angles:

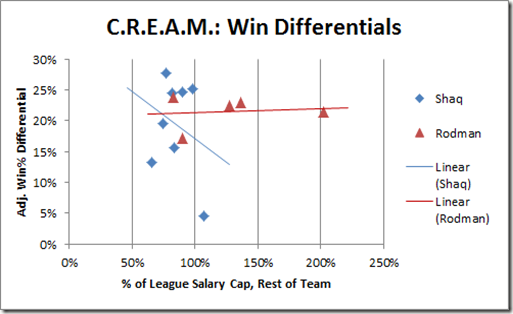
Angle 1: Money (again)

The following graph is similar to my ROI graph above, except instead of mapping the player’s salary to his win differential, I’m mapping the rest of the team’s salary to his win differential:

^{Note: Though obviously it’s only one data point and doesn’t mean anything, I find it amusing that the one time Shaq played for a team that had a full salary-cap’s worth of players without him, his win differential dropped to the floor.}

So, basically, whether Rodman’s teams were broke or flush, his impact remained fairly constant. This is consistent with unusually low diminishing returns.

Angle 2: Position (again)

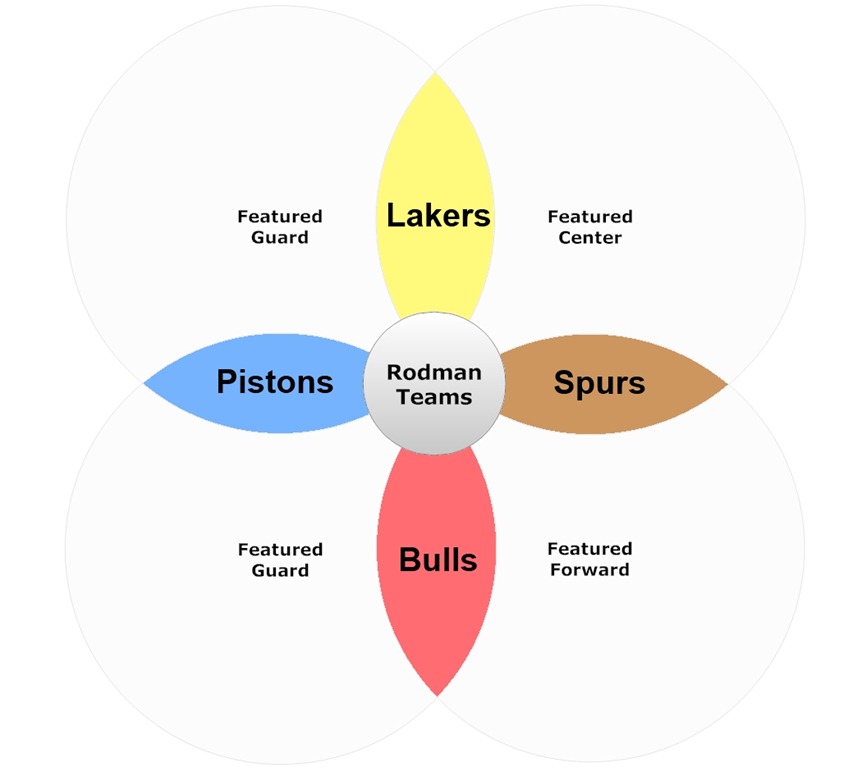
A potential objection I’ve actually heard a couple of times is that perhaps Rodman was able to have the impact he did because the circumstances he played in were particularly well-suited to never duplicating his skill-set: E.g., both Detroit and Chicago lacked dominant big men. Indeed, it’s plausible that part of his value came from providing the defense/rebounding of a dominant center, maximally leveraging his skill-set, and freeing up his teams to go with smaller, more versatile, and more offense-minded players at other positions (which could help explain why he had a greater impact on offensive efficiency than on defensive efficiency). However, all of this value would be visible. Moreover, the assumption that Rodman only played in these situations is false. Not only did Rodman play on very different teams with very different playing styles, he actually played on teams with every possible combination of featured players (or “1st and 2nd-best” players, if you prefer):

As we saw above, Rodman’s impact on all 4 teams was roughly the same. This too is consistent with an unusual lack of diminishing returns.

Evidence of Cause:

As I’ve said earlier, “role” can be very hard to define in the NBA relative to other sports. But to find meaningful evidence that Rodman provided an inordinate amount of value for his role, we don’t necessarily need to solve this intractable problem: we can instead look for “partial” or “imperfect” proxies. If some plausibly related proxy were to provide an unusual enough result, its actual relationship to the posited scenario could be self-reinforced—that is, the most likely explanation for the extremely unlikely result could be that it IS related to our hypothesis AND that our hypothesis is true.

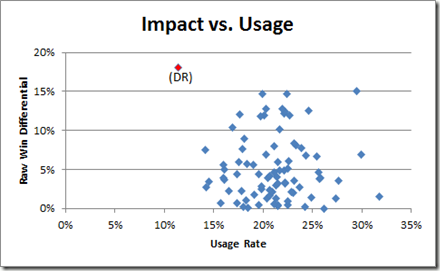
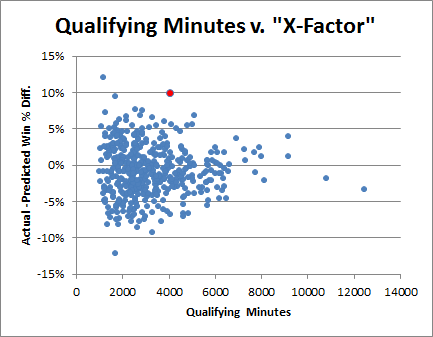
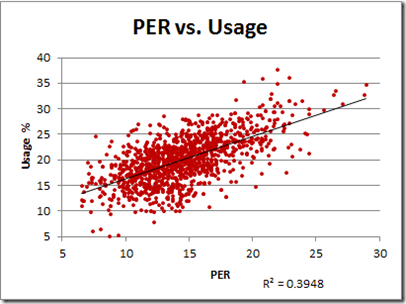
So one scarce resource that is plausibly related to role is “usage.” Usage Rate is the percentage of team possessions that a player “uses” by taking a shot or committing a turnover. Shooters obviously have higher usage rates than defender/rebounders, and usage generally has little correlation with impact. But let’s take a look at a scatter-plot of qualifying players from my initial differential study (limited to just those who have positive raw win differentials):

The red dot is obviously Dennis Rodman. Bonus points to anyone who said “Holy Crap” in their heads when they saw this graph: Rodman has both the highest win differential and the lowest Usage Rate, once again taking up residence in Outlier Land.

Let’s look at it another way: Treating possessions as the scarce resource, we might be interested in how much win differential we get for every possession that a player uses:

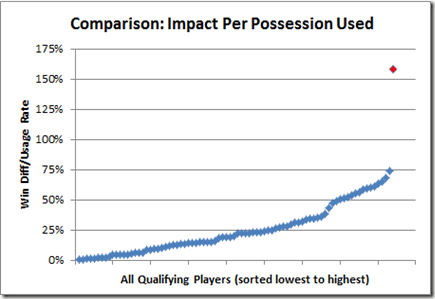
Let me say this in case any of you forgot to think it this time:

“Holy Crap!”

Yes, the red dot is Dennis Rodman. Oh, if you didn’t see it, don’t follow the blue line, it won’t help.

This chart isn’t doctored, manipulated, or tailored in any way to produce that result, and it includes all qualifying players with positive win differentials. If you’re interested, the Standard Deviation on the non-Rodman players in the pool is .19. Yes, that’s right, Dennis Rodman is nearly 4.5 standard deviations above the NEXT HIGHEST player. Hopefully, you see the picture of what could be going on here emerging: If value per possession is any kind of proxy (even an imperfect one) for value relative to role, it goes a long way toward explaining how Rodman was able to have such incredible impacts on so many teams with so many different characteristics.

The irony here is that the very aspect of Rodman’s game that frequently causes people to discount his value (“oh, he only does one thing”) may be exactly the quality that makes him a strong contender for first pick on the all-time NBA playground.

Conclusions:

Though the evidence is entirely circumstantial, I find the hypothesis very plausible, which in itself should be shocking. While I may not be ready to conclude that, yes, in fact, Rodman would actually be a more valuable asset to a potential championship contender than Michael freaking Jordan, I don’t think the opposite view is any stronger: That is, when you call that position crazy, conjectural, speculative, or naïve—as some of you inevitably will—I am fairly confident that, in light of the evidence, the default position is really no less so.

In fact, even if this hypothesis isn’t exactly true, I don’t think the next-most-likely explanation is that it’s completely false, and these outlandish outcomes were just some freakishly bizarre coincidence—it would be more likely that there is some alternate explanation that may be even more meaningful. Indeed, on some level, some of the freakish statistical results associated with Rodman are so extreme that it actually makes me doubt that the best explanation could actually stem from his athletic abilities. That is, he’s just a guy, how could he be so unusually good in such an unusual way? Maybe it actually IS more likely that the groupthink mentality of NBA coaches and execs accidentally DID leave a giant exploitable loophole in conventional NBA strategy; a loophole that Rodman fortuitously stumbled upon by having such a strong aversion to doing any of the things that he wasn’t the best at. If that is the case, however, the implications of this series could be even more severe than I intended.

Series Afterword:

Despite having spent time in law school, I’m not a lawyer. Indeed, one of the reasons I chose not to be one is because I get icky at the thought of picking sides first, and building arguments later.

In this case, I had strong intuitions about Rodman based on a variety of beliefs I had been developing about basketball value, combined with a number of seemingly-related statistical anomalies in Rodman’s record. Though I am naturally happy that my research has backed up those intuitions—even beyond my wildest expectations—I felt prepared for it to go the other way. But, of course, no matter how hard we try, we are all susceptible to bias.

Moreover, inevitably, certain non-material choices (style, structure, editorial, etc.) have to be made which emphasize the side of the argument that you are trying to defend. This too makes me slightly queasy, though I recognize it as a necessary evil in the discipline of rhetoric. My point is this: though I am definitely presenting a “case,” and it often appears one-sided, I have tried to conduct my research as neutrally as possible. If there is any area where you think I’ve failed in this regard, please don’t hesitate to let me know. I am willing to correct myself, beef up my research, or present compelling opposing arguments alongside my own; and though I’ve published this series in blog form, I consider this Case to be an ongoing project.

If you have any other questions, suggestions, or concerns, please bring them up in the comments (preferably) or email me and I will do my best to address them.

Finally, I would like to thank Nate Meyvis, Leo Wolpert, Brandon Wall, James Stuart, Dana Powers, and Aaron Nathan for the invaluable help they provided me by analyzing, criticizing, and/or ridiculing my ideas throughout this process. I’d also like to thank Jeff Bennett for putting me on this path, Scott Carder for helping me stay sane, and of course my wife Emilia for her constant encouragement.

The Case for Dennis Rodman, Part 4/4(a): All-Hall?

First of all, congrats to Dennis for his well-deserved selection as a 2011 Hall of Fame inductee—of course, I take full credit. But seriously, when the finalists were announced, I immediately suspected that he would make the cut, mostly for two reasons:

Making the finalists this year after failing to make the semi-finalists last year made it more likely that last year’s snub really was more about eligibility concerns than general antipathy or lack of respect toward him as a player.
The list of co-finalists was very favorable. First, Reggie Miller not making the list was a boon, as he could have taken the “best player” spot, and Rodman would have lacked the goodwill to make it as one of the “overdue”—without Reggie, Rodman was clearly the most accomplished name in the field. Second, Chris Mullen being available to take the “overdue” spot was the proverbial “spoonful of sugar” that allowed the bad medicine of Rodman’s selection go down.

Congrats also to Artis Gilmore and Arvydas Sabonis. In my historical research, Gilmore’s name has repeatedly popped up as an excellent player, both by conventional measures (11-time All-Star, 1xABA Champion, 1xABA MVP, led league in FG% 7 times), and advanced statistical ones (NBA career leader in True Shooting %, ABA career leader in Win Shares and Win Shares/48, and a great all-around rebounder). It was actually only a few months ago that I first discovered—to my shock—that he was NOT in the Hall [Note to self: cancel plans for “The Case for Artis Gilmore”]. Sabonis was an excellent international player with a 20+ year career that included leading the U.S.S.R. to an Olympic gold medal and winning 8 European POY awards. I remember following him closely when he finally came to the NBA, and during his too-brief stint, he was one of the great per-minute contributors in the league (though obviously I’m not a fan of the stat, his PER over his first 5 season—which were from age 31-35—was 21.7, which would place him around 30th in NBA history). Though his sample size was too small to qualify for my study, his adjusted win percentage differential over his NBA career was a very respectable 9.95%, despite only averaging 24 minutes per game.

I was hesitant to publish Part 4 of this series before knowing whether Rodman made the Hall or not, as obviously the results shape the appropriate scope for my final arguments. So by necessity, this section has changed dramatically from what I initially intended. But I am glad I waited, as this gives me the opportunity to push the envelope of the analysis a little bit: Rather than simply wrapping up the argument for Rodman’s Hall-of-Fame candidacy, I’m going to consider some more ambitious ideas. Specifically, I will articulate two plausible arguments that Rodman may have been even more valuable than my analysis so far has suggested. The first of these is below, and the second—which is the most ambitious, and possibly the most shocking—will be published Monday morning in the final post of this series.

Introduction

I am aware that I’ve picked up a few readers since joining “the world’s finest quantitative analysts of basketball” in ESPN’s TrueHoop Stat Geek Smackdown. If you’re new, the main things you need to know about this series are that it’s 1) extremely long (sprawling over 13 sections in 4 parts, plus a Graph of the Day), 2) ridiculously (almost comically) detailed, and 3) only partly about Dennis Rodman. It’s also a convenient vehicle for me to present some of my original research and criticism about basketball analysis.

Obviously, the series includes a lot of superficially complicated statistics, though if you’re willing to plow through it all, I try to highlight the upshots as much as possible. But there is a lot going on, so to help new and old readers alike, I have a newly-updated “Rodman Series Guide,” which includes a broken down list of articles, a sampling of some of the most important graphs and visuals, and as of now, a giant new table summarizing the entire series by post, including the main points on both sides of the analysis. It’s too long to embed here, but it looks kind of like this:

As I’ve said repeatedly, this blog isn’t just called “Skeptical” Sports because the name was available: When it comes to sports analysis—from the mundane to the cutting edge—I’m a skeptic. People make interesting observations, perform detailed research, and make largely compelling arguments—which is all valuable. The problems begin when then they start believing too strongly in their results: they defend and “develop” their ideas and positions with an air of certainty far beyond what is objectively, empirically, or logically justified.

With that said, and being completely honest, I think The Case For Dennis Rodman is practically overkill. As a skeptic, I try to keep my ideas in their proper context: There are plausible hypotheses, speculative ideas, interim explanations requiring additional investigation, claims supported by varying degrees of analytical research, propositions that have been confirmed by multiple independent approaches, and the things I believe so thoroughly that I’m willing to write 13-part series’ to prove them. That Rodman was a great rebounder, that he was an extremely valuable player, even that he was easily Hall-of-Fame caliber—these propositions all fall into that latter category: they require a certain amount of thoughtful digging, but beyond that they practically prove themselves.

Yet, surely, there must be a whole realm of informed analysis to be done that is probative and compelling but which might fall short of the rigorous standards of “true knowledge.” As a skeptic, there are very few things I would bet my life on, but as a gambler—even a skeptical one—there are a much greater number of things I would bet my money on. So as my final act in this production, I’d like to present a couple of interesting arguments for Rodman’s greatness that are both a bit more extreme and a bit more speculative than those that have come before. Fortunately, I don’t think it makes them any less important, or any less captivating:

Read the rest of this entry »

MIT Sloan Sports Analytics Conference, Day 1: Recap and Thoughts

This was my first time attending this conference, and Day 1 was an amazing experience. At this point last year, I literally didn’t know that there was a term (“sports analytics”) for the stuff I liked to do in my spare time. Now I learn that there is not only an entire industry built up around the practice, but a whole army of nerds in its society. Naturally, I have tons of criticisms of various things that I saw and heard—that’s what I do—but I loved it, even the parts I hated.

Here are the panels and presentations that I attended, along with some of my thoughts:

Birth to Stardom: Developing the Modern Athlete in 10,000 Hours?

Featuring Malcolm Gladwell (Author of Outliers), Jeff Van Gundy (ESPN), and others I didn’t recognize.

In this talk, Gladwell rehashed his absurdly popular maxim about how it takes 10,000 hours to master anything, and then made a bunch of absurd claims about talent. (Players with talent are at a disadvantage! Nobody wants to hire Supreme Court clerks! Etc.) The most re-tweeted item to come out of Day 1 by far was his highly speculative assertion that “a lot of what we call talent is the desire to practice.”

While this makes for a great motivational poster, IMO his argument in this area is tautological at best, and highly deceptive at worst. Some people have the gift of extreme talent, and some people have the gift of incredible work ethic. The streets of the earth are littered with the corpses of people who had one and not the other. Unsurprisingly, the most successful people tend to have both. To illustrate, here’s a random sample of 10,000 “people” with independent normally distributed work ethic and talent (each with a mean of 0, standard deviation of 1):

The blue dots (left axis) are simply Hard Work plotted against Talent. The red dots (right axis) are Hard Work plotted against the sum of Hard Work and Talent—call it “total awesome factor” or “success” or whatever. Now let’s try a little Bayes’ Theorem intuition check: You randomly select a person and they have an awesome factor of +5. What are the odds that they have a work ethic of better than 2 standard deviations above the mean? High? Does this prove that all of the successful people are just hard workers in disguise?

Hint: No. And this illustration is conservative: This sample is only 10,000 strong: increase to 10 billion, and the biggest outliers will be even more uniformly even harder workers (and they will all be extremely talented as well). Moreover, this “model” for greatness is just a sum of the two variables, when in reality it is probably closer to a product, which would lead to even greater disparities. E.g.: I imagine total greatness achieved might be something like great stuff produced per minute worked (a function of talent) times total minutes worked (a function of willpower, determination, fortitude, blah blah, etc).

The general problem with Gladwell I think is that his emphatic de-emphasis of talent (which has no evidence backing it up) cheapens his much stronger underlying observation that for any individual to fully maximize their potential takes the accumulation of a massive amount of hard work—and this is true for people regardless of what their full potential may be. Of course, this could just be a shrewd marketing ploy on his part: you probably sell more books by selling the hope of greatness rather than the hope of being an upper-level mid-manager (especially since you don’t have to worry about that hope going unfulfilled for at least 10 years).

Read the rest of this entry »

The Case for Dennis Rodman, Part 3/4(b)—Rodman’s X-Factor

The sports analytical community has long used Margin of Victory or similar metrics as their core component for predicting future outcomes. In situations with relatively small samples, it generally slightly outperforms win percentages, even when predicting win percentages.

There are several different methods for converting MOV into expected win-rates. For this series, I took the 55,000+ regular-season team games played since 1986 and compared their outcomes to the team’s Margin of Victory over the other 81 games of the season. I then ran this data through a logistic regression (a method for predicting things that come in percentages) with MOV as the predictor variable. Here is the resulting formula:

$\large{PredictedWin\% = \dfrac{1}{1+e^{-(.127mv-.004}}}$

^{Note: e is euler’s number, or ~2.72. mv is the variable for margin of victory.}

This will return the probability between 0 and 1, corresponding to the odds of winning the predicted game. If you want to try it out for yourself, the excel formula is:

1 / (1 + EXP(-(-0.0039+0.1272*[MOV])))

So, for example, if a team’s point differential (MOV) over 81 games is 3.78 points per game, their odds of winning their 82nd game would be 61.7%.

Of course, we can use this same formula to predict a player’s win% differential based on his MOV differential. If, based on his MOV contribution alone, a player’s team would be expected to win 61.7% of the time, then his predicted win% differential is what his contribution would be above average, in this case 11.7% (this is one reason why, for comparison purposes, I prefer to use adjusted win differentials, as discussed in Part 3(a)).

As discussed in the part 2(b) of this series (“With or Without Worm”), Dennis Rodman’s MOV differential was 3.78 points, which was tops among players with at least a season’s worth of qualifying data, corresponding to the aforementioned win differential of 11.7%. Yet this under-predicts his actual win percentage differential by 9.9%. This could be the result of a miscalibrated prediction formula, but as you can see in the following histogram, the mean for win differential minus predicted win differential for our 470 qualifying player dataset is actually slightly below zero at –0.7%:

Rodman has the 2nd highest overall, which is even more crazy considering that he had one of the highest MOV’s (and the highest of anyone with anywhere close to his sample size) to begin with. Note how much of an outlier he is in this scatterplot (red dot is Rodman):

I call this difference the “X-Factor.” For my purposes, “X” stands for “unknown”: That is, it is the amount of a player’s win differential that isn’t explained by the most common method for predicting win percentages. For any particular player, it may represent an actual skill for winning above and beyond a player’s ability to contribute to his team’s margin of victory (in section (c), I will go about proving that such a skill exists), or it may simply be a result of normal variance. But considering that Rodman’s sample size is significantly larger than the average in our dataset, the chances of it being “error” should be much smaller. Consider the following:

Again, Rodman is a significant outlier: no one with more than 2500 qualifying minutes breaks 7.5%. Rodman’s combination of large sample with large Margin of Victory differential with large X-Factor is remarkable. To visualize this, I’ve put together a 3-D scatter plot of all 3 variables:

It can be hard to see where a point stands in space in a 2-D image, but I’ve added a surface grid to try to help guide you: the red point on top of the red mountain is Dennis Rodman.

To get a useful measure of how extreme this is, we can approximate a sample-size adjustment by comparing the number of qualifying minutes for each player to the average for the dataset, and then adjusting the standard deviation for that player accordingly (proportional to the square root of the ratio, a method which I’ll discuss in more detail in section (d)). After doing this, I can re-make the same histogram as above with the sample-adjusted numbers:

No man is an island. Except, apparently, for Dennis Rodman. Note that he is about 4 standard deviations above the mean (and observe how the normal distribution line has actually blended with the axis below his data point).

Naturally, of course, this raises the question:

Where does Rodman’s X-Factor come from?

Strictly speaking, what I’m calling “X-Factor” is just the prediction error of this model with respect to players. Some of that error is random and some of it is systematic. In section (c), I will prove that it’s not entirely random, though where it comes from for any individual player, I can only speculate.

Margin of Victory treats all contributions to a game’s point spread equally, whether they came at the tail end of a blowout, or in the final seconds of squeaker. One thing that could contribute to a high X-factor is “clutch”ness. A “clutch” shooter (like a Robert Horry), for example, might be an average or even slightly below-average player for most of the time he is on the floor, but an extremely valuable one near the end of games that could go either way. The net effect from the non-close games would be small for both metrics, but the effect of winning close games would be much higher on Win% than MOV. Of course, “clutch”ness doesn’t have to be limited to shooters: e.g., if one of a particular player’s skill advantages over the competition is that he makes better tactical decisions near the end of close games (like knowing when to intentionally foul, etc.), that would reflect much more strongly in his W% than in his MOV.

Also, a player who contributes significantly whenever they are on the floor but is frequently taken out of non-close games as a precaution again fatigue or injury may have a Win % that accurately reflects his impact, but a significantly understated MOV. E.g., in the Boston Celtics “Big 3” championship season, Kevin Garnett was rested constantly—a fact that probably killed his chances of being that season’s MVP—yet the Celtics won by far the most games in the league. In this case, the player is “clutch” just by virtue of being on the floor more in clutch spots.

The converse possibility also exists: A player could be “reverse clutch,” meaning that he plays worse when the game is NOT on the line. This would ultimately have the same statistical effect as if he played better in crunch time. And indeed, based on completely non-rigorous and anecdotal speculation, I think this is a possible factor in Rodman’s case. During his time in Chicago, I definitely recall him doing a number of silly things in the 4th quarter of blowout games (like launching up ridiculous 3-pointers) when it didn’t matter—and in a game of small margins, these things add up.

Finally, though it cuts a small amount against the absurdity of Rodman’s rebounding statistics, I would be derelict as an analyst not to mention the possibility that Rodman may have played sub-optimally in non-close games in order to pad his rebounding numbers. The net effect, of course, would be that his rebounding statistics could be slightly overstated, while his value (which is already quite prodigious) could be substantially understated. To be completely honest, with his rebounding percentages and his X-Factor both being such extreme outliers, I have to think that at least some relationship existing between the two is likely.

If you’re emotionally attached to the freak-alien-rebounder hypothesis, this might seem to be a bad result for you. But if you’re interested in Rodman’s true value to the teams he played for, you should understand that, if this theory is accurate, it could put Rodman’s true impact on winning into the stratosphere. That is, this possibility gives no fuel to Rodman’s potential critics: the worst cases on either side of the spectrum are that Rodman was the sickest rebounder with a great impact on his teams, or that he was a great rebounder with the sickest impact.

In the next section, I will be examining the relative reliability and importance of Margin of Victory vs. Win % generally, across the entire league. In my “endgame” analysis, this is the balance of factors that I will use. But the league patterns do not necessarily apply in all situations: In some cases, a player’s X-factor may be all luck, in some cases it may be all skill, and in most it is probably a mixture of both. So, for example, if my speculation about Rodman’s X-Factor were true, my final analysis of Rodman’s value could be greatly understated.

The Case for Dennis Rodman, Part 2/4 (b)—With or Without Worm

I recently realized that if I don’t speed up my posting of this series, Rodman might actually be in the Hall of Fame before I’m done. Therefore, I’m going to post this section now, and Part 3 (which will probably only be one post) in the next few days.

This blog is called “Skeptical” Sports Analysis for a reason: I’m generally wary of our ability to understand anything definitively, and I believe that most people who confidently claim to know a lot of things other than facts—whether in sports, academics, or life—are either lying, exaggerating, or wrong. I don’t accept this as an a priori philosophical tenet (in college I was actually very resistant to the skeptics), but as an empirical conclusion based on many years of engaging and analyzing various people’s claims of knowledge. As any of you who happen to know me will attest, if I have any talent on this earth, it is finding fault with such claims (even when they are my own).

Keeping that in mind—and keeping in mind that, unlike most sports commentators, I don’t offer broadly conclusive superlatives very often—I offer this broadly conclusive superlative: Dennis Rodman was the greatest rebounder of all time. If there has been any loose end in the arguments I’ve made already, it is this: based on the evidence I’ve presented so far, Rodman’s otherworldly rebounding statistics could, theoretically, be a result of shenanigans. That is, he could simply have been playing at the role of rebounder on his teams, ignoring all else and unnaturally inflating his rebounding stats, while only marginally (or even negatively) contributing to his team’s performance. Thus, the final piece of this puzzle is showing that his rebounding actually helped his teams. If that could be demonstrated, then even my perversely skeptical mind would be satisfied on the point—else there be no hope for knowledge.

This is where “The Case for Dennis Rodman Was a Great Rebounder” and “The Case for Dennis Rodman” join paths: Showing that Rodman got a lot of rebounds without also showing that this significantly improved his teams proves neither that he was a great player nor that he was a great rebounder. Unfortunately, as I discussed in the last two sections, player value can be hard to measure, and the most common conventional and unconventional valuation methods are deeply flawed (not to mention unkind toward Rodman). Thus, in this post and the next, I will take a different approach.

Differential (Indirect) Statistics

For this analysis, I will not be looking at Dennis Rodman’s (or any other player’s) statistics directly at all. Instead, I will be looking at his team’s statistics, comparing the games in which he played to the games that he missed. I used a similar (though simpler) method in my mildly popular Quantum Randy Moss post last fall, which Brian Burke dubbed WOWRM, or “With or Without Randy Moss.” So, now I present that post’s homophonic cousin: WOWWorm, or “With or Without Worm.”

The main advantages to indirect statistics are that they are all-inclusive (everything good or bad that a player does is accounted for, whether it is reflected in the box score or not), empirical (what we do or don’t know about the importance of various factors doesn’t matter), and they can get you about as close as possible in this business to isolating actual cause and effect. These features make the approach especially trenchant for general hypothesis-testing and broader studies of predictivity that include league-wide data.

The main disadvantage for individual player analysis, however, is that the samples are almost always too small to be conclusive (in my dream universe, every player would be forced to sit out half of their team’s regular-season games at random). They are also subject to bias based on quality of the player’s team (it is harder to have a big impact on a good team), or based on the quality of their backup—though I think the latter effect is much smaller in the basketball than in football or baseball. In the NBA, teams rotate in many different players and normally have a lot of different looks, so when a starter goes out, they’re rarely just replaced by one person—the whole roster (even the whole gameplan) may shift around to exploit the remaining talent. This is one reason you almost never hear of an NBA bench player finally “getting his shot” because the player in front of them was injured—if someone has exploitable skills, they are probably going to get playing time regardless. Fortunately, Dennis Rodman missed his fair share of games—aided by his proclivity for suspensions—and the five seasons in which he missed at least 15 games came on four different teams.

Note, for the past few years, more complete data has allowed people to look at minute-by-minute or play-by-play +/- in basketball (as has been done for some time in hockey). This basically eliminates the sample size problem, though it introduces a number of potential rotational, strategic and role-based biases. Nevertheless, it definitely makes for a myriad of exciting analytical possibilities.

Margin of Victory

For structural reasons, I’m going to hold off on Rodman’s Win % differentials until my next post in this series. In this post, however, I will look at everything else, starting with team point differential differential—a.k.a. “Margin of Victory”:

^{Note: Table is only the top 25 players in the dataset.}

First, the nitty-gritty: This data goes back to 1986, starting with all players who missed and played at least 15 games in a single season while averaging at least 20 minutes per game played. The “qualifying games” in a season is the smaller of games played or games missed. E.g., if someone played 62 games and missed 20, that counts as 20 qualifying games, the same as if someone played 20 games and missed 62. Their “qualifying minutes” are then their average of minutes per game played multiplied by their total number of qualifying games. For the sample, I set the bar at 3000 qualifying minutes, or roughly the equivalent of a full season for a typical starter (82 games * 36 minutes/game is 2952 minutes), which leaves 164 qualifying players. I then calculated differentials for each team-season: I.e., per-game averages were calculated separately for the set of games played and the set of games missed by each player from within a particular season, and each season’s “differentials” were created for each stat simply by subtracting the second from the first. Finally, I averaged the per-season differentials for each qualifying season for each player. This is necessarily different from how multiple-season per-game stats are usually calculated (which is just to sum up the stats from the various seasons and divide by total games). As qualifying games may come from different teams and different circumstances, to isolate a player’s impact it is crucially important that (as much as possible) their presence or absence is the only variable that changes, which is not even remotely possible across multiple seasons. In case anyone is interested, here is the complete table with all differential stats for all 164 qualified players.

I first ran the differentials for Dennis Rodman quite some time ago, so I knew his numbers were very good. But when I set out to do the same thing for the entire league, I had no idea that Rodman would end up literally on top. Here is a histogram of the MOV-differential distribution for all qualified players (rounded to the nearest .5):

^{Note: Red is Dennis Rodman (and Ron Artest).}

3.8 points per game may not sound like much compared to league-leading scorers who score 30+, but that’s both the beauty of this method and the curse of conventional statistics: When a player’s true impact is actually only a few points difference per night (max), you know that the vast majority of the “production” reflected in their score line doesn’t actually contribute to their team’s margin.

This deserves a little teasing out, as the implications can be non-obvious: If a player who scores 30 points per game is only actually contributing 1 or 2 points to his team’s average margin, that essentially means that at least 28 of those points are either 1) redundant or 2) offset by other deficiencies. With such a low signal-to-noise ratio, you should be able to see how how it is that pervasive metrics like PER can be so unreliable: If a player only scores 10 points a night, but 4 of them are points his team couldn’t have scored otherwise, he could be contributing as much as Shaquille O’Neal. Conversely, someone on the league leaderboard who scores 25 points per game could be gaining his team 2 or 3 points a night with his shooting, but then be giving it all back if he’s also good for a couple of unnecessary turnovers.

Professional basketball is a relatively low-variance sport, but winners are still determined by very small margins. Last year’s championship Lakers team had an average margin of victory of just 4.7 points. For the past 5 years, roughly three quarters of teams have had lower MOV’s than Dennis Rodman’s differential in his 5 qualifying seasons:

Now, I don’t want to suggest too much with this, but I would be derelict if I didn’t mention the many Hall of Fame-caliber players who qualified for this list below Rodman (my apologies if I missed anyone):

In HoF already:

Hakeem Olajuwon
Scottie Pippen<
Clyde Drexler
Dominique Wilkins

HoF locks:

Shaquille O’Nea
Dwyane Wade
Jason Kidd
Allen Iverson
Ray Allen

HoF possible:

Yao Ming
Pau Gasol
Marcus Camby
Carlos Boozer
Alonzo Mourning

Not in HoF but probably should be:

Toni Kukoc
Chris Mullin
Tim Hardaway
Dikembe Mutumbo

The master list also likely includes many players that are NOT stars but who quietly contributed a lot more to their teams than people realize. Add the fact that Rodman managed to post these differentials while playing mostly for extremely good, contending, teams (where it is harder to have a measurable impact), and was never ostensibly the lynchpin of his team’s strategy—as many players on this list certainly were—and it is really quite an amazing outcome.

Now, I do not mean to suggest that Rodman is actually the most valuable player to lace up sneakers in the past 25 years, or even that he was the most valuable player on this list: 1) It doesn’t prove that, and 2) I don’t think that. Other more direct analysis that I’ve done typically places him “only” in the top 5% or so of starting players. There is a lot of variance in differential statistics, and there are a lot of different stories and circumstances involved for each player. But, at the very least, this should be a wake-up call for those who ignore Rodman for his lack of scoring, and for those who dismiss him as “merely” a role-player.

Where Does His Margin Come From?

As I have discussed previously, one of the main defenses of conventional statistics—particularly vis a vis their failures w/r/t Dennis Rodman—is that they don’t account for defense or “intangibles.” As stated in the Wikipedia entry for PER:

Neither PER nor per-game statistics take into account such intangible elements as competitive drive, leadership, durability, conditioning, hustle, or WIM (wanting it more), largely because there is no real way to quantitatively measure these things.

This is true, for the most part—but not so much for Rodman. He does very well with indirect statistics, which actually DO account for all of these things as part of the gestalt that goes into MOV or Win% differentials. But these stats also give us a very detailed picture of where those differences likely come from. Here is a table summarizing a number of Rodman’s differential statistics, both for his teams and their opponents. The “reciprocal advantage” is the difference between his team’s differential and their opponent’s differential for the same statistic:

^{Note: Some of the reciprocals were calculated in this table, and others are taken from the dataset (like margin of victory). In the latter case, they may not necessarily match up perfectly, but this is for a number of technical and mathematical reasons that have no significant bearing on the final outcomes.}

Rodman’s Margin of Victory differential comes in part from his teams scoring more points on offense and in part from their allowing fewer points on defense. Superficially, this may look like the majority of Rodman’s impact is coming on the defensive side (-2.4 vs. + 1.3), but that’s deceptive. As you can find in the master table, Rodman also has a significant negative effect on “Pace”—or number of possessions per game—which basically applies equally to both teams. This is almost certainly due to his large number of possession-extending offensive rebounds, especially as he was known (and sometimes criticized) for “kicking it out” and resetting the offense rather than trying to shoot it himself or draw a foul. “Scoring opportunities” are total possessions plus offensive rebounds. As you might expect intuitively, his teams generally had about the same number of these with or without him, because the possessions weren’t actually lost, they were only restarted.

As we can see from the reciprocal table, Rodman had a slightly positive effect on his teams scoring efficiency (points per opportunity), but also had a small positive (though nearly negligible) effect on his opponents’. Thus, combining the effect his rebounding had on number of scoring opportunities with any other effects he had on each side’s scoring efficiency, we can get a fairly accurate anatomy of his overall margin. In case that confused you, here it is broken down step-by-step:

So, roughly speaking, his 3.7ish margin of victory breaks down to roughly 2.8 points from effect on offensive and defensive scoring opportunities and .9 points from the actual value of those opportunities—or, visually:

Furthermore, at least part of that extra offensive efficiency likely stems from the fact that a larger proportion of those scoring opportunities began as offensive rebounds, and post-offensive-rebound “possessions” are typically worth slightly more than normal (though this may actually be less true with Rodman due to the “kicking”). Otherwise, the exact source of the efficiency differences is much more uncertain, especially as the smaller margins in the other statistics are that much more unreliable because of the sample-size issues inherent in this method.

The next-strongest reciprocal effects on the list above appear to be personal fouls and their corresponding free throws: with him in the lineup, his teams had fewer fouls and more free throws, and his opponents the opposite. This is particularly peculiar because Rodman himself got a lot of fouls and was a terrible free throw shooter (note: this is yet another reason why including personal fouls in your player valuation method—yes, I’m looking at you, PER—is ridiculous).

Whether Rodman was a “role player” or not is irrelevant: whatever his role, he did it well enough to contribute more to his teams than the vast majority of NBA players (role players or not) contributed to theirs. For some reason, this simple concept seems to be better understood in other sports: No-one would say that Mariano Rivera hasn’t contributed much to the Yankees winning because he is “merely” a closer (though I do think he could contribute more if he pitched more innings), just as no-one would say that Darrelle Revis hasn’t contributed much to the Jets because he is “merely” a cornerback.

So does this mean I am conceding that Rodman was just a very good, but one-dimensional, player? Not that there would be anything wrong with that, but definitely not. That is how I would describe it if he had hurt his team in other areas, but then made up for it—and then some—through excellent rebounding. This is actually probably how most people would predict that Rodman’s differentials would break down (including, initially, myself), but they don’t. E.g., the fact that his presence on the court didn’t hurt his team’s offensive efficiency, despite hardly ever scoring himself, is solid evidence that he was actually an excellent offensive player. Even if you take the direct effects of his rebounds out of the equation entirely, he still seems to have made three different championship contenders—including one of the greatest teams of all time—better. While the majority of his value added—that which enabled him to significantly improve already great teams—came from his ability to grab rebounds that no one else would have gotten, the full realization of that value was made possible by his not hurting those teams significantly in any other way.

As it wasn’t mystical intangibles or conveniently immeasurable defensive ability that made Rodman so valuable, I think it is time we rescind the free pass given to the various player valuation metrics that have relied on that excuse for getting this one so wrong for so long. However, this does not prove that even a perfectly-designed metric would necessarily be able to identify this added value directly. Though I think valuation metrics can be greatly improved (and I’m trying to do so myself), I can’t say for certain that my methods or any others will definitely be able to identify which rebounds actually helped a team get more rebounds and which points actually helped a team score more points. Indeed, a bench player who scores 8 points per game could be incredibly valuable if they were the right 8 points, even if there were no other direct indications (incidentally, this possibility has been supported by separate research I’ve been doing on play-by-play statistics from the last few seasons, in which I’ve found that a number of bench players have contributed much more to their teams than most people would have guessed possible). But rather than throwing our hands in the air and defending inadequate pre-existing approaches, we should be trying to figure out how and whether these sorts of problems can be addressed.

Defensive Stalwart or Offensive Juggernaut?

As an amusing but relevant aside, you may have already noticed that the data—at least superficially—doesn’t even seem to support the conventional wisdom that, aside from his rebounding, Rodman was primarily a defensive player. Most obviously, his own team’s points per scoring opportunity improved, but his opponents’ improved slightly as well. If his impact were primarily felt on the defensive side, we would probably expect the opposite. Breaking down the main components above into their offensive and defensive parts, our value-source pie-chart would look like this.

The red is actually slightly smaller than his contribution from defensive rebounds alone, as technically defensive efficiency was slightly lower with Rodman in the games. For fun, I’ve broken this down a bit further into an Offense vs. Defense “Tale of the Tape,” including a few more statistics not seen above:

^{Note: Differentials that help their respective side are highlighted in blue, and those that hurt their respective side are highlighted in Red. The values for steals and blocks are each transposed from their team and opponent versions above, as these are defensive statistics to begin with.}

Based on this completely ridiculous and ad-hoc analysis, it would seem that Rodman was more of an offensive player than a defensive one.

Including rebounding, I suspect it is true that Rodman’s overall contribution was greater on offense than defense. However, I wouldn’t read too much into the breakdowns for each side. Rodman’s opponents scoring slightly more per opportunity with him in the game does NOT prove that he was a below-average defender. Basketball is an extremely dynamic game, and the effects of success in one area may easily be realized in others. For example, a strong defensive presence may free up other players to focus on their team’s offense, in which case the statistical consequences could be seen on the opposite side of the floor from where the benefit actually originated.

There are potential hints of this kind of possibility in this data, such as: Why on earth would Rodman’s teams shoot better from behind the arc, considering that he was only a .231 career 3-point shooter himself? This could obviously just be noise, but it’s also possible that some underlying story exists in which more quality long-range shots opened up as a result of Rodman’s successes in other assignments. Ultimately, I don’t think we can draw any conclusions on the issue, but the fact that this is even a debatable question has interesting implications, both for Dennis Rodman and for basketball analytics broadly.

Conclusions

While I am the first to admit that the dataset this analysis is based on might not be sufficiently robust to settle the entire “Case” on its own, I still believe these results are powerful evidence of the truth of my previous inferences—and for very specific reasons:

Assessing the probability of propositions that have a pre-conceived likelihood of being true in light of new evidence can be tricky business. In this case, the story goes like this: I developed a number of highly plausible conclusions about Rodman’s value based on a number of reasonable observations and empirical inquiries, such as: 1) the fact that his rebounding prowess was not just great, but truly extreme, 2) the fact that his teams always seemed to do extremely well on both ends of the floor, and 3) my analysis (conducted for reasons greater than just this series) suggesting that A) scoring is broadly overrated, B) rebounding is broadly underrated, and C) that rebounding has increasing marginal returns (or is exponentially predictive). Then, to further examine these propositions, I employed a completely independent method—having virtually no overlap with the various factors involved in those previous determinations—and it not only appears to confirm my prior beliefs, but does so even more than I imagined it would.

Now, technically, it is possible that Rodman just got extremely lucky in the differential data—in fact, for this sample size, getting that lucky isn’t even a particularly unlikely event, and many of his oddball compatriots near the top of the master list probably did just that. But this situation lends itself perfectly to Bayes’ Theorem-style analysis. That is, which is the better, more likely explanation for this convergence of results: 1) that my carefully reasoned analysis has been completely off-base, AND that Rodman got extremely lucky in this completely independent metric, or 2) that Dennis Rodman actually was an extremely valuable player?

Google Search of the Day: Player Efficiency Rating is Useless

From the “almost too good to be true” department:

Hat tip to whoever the guy was that used that search to find my blog yesterday. See for yourself here.

Note the irony that I’m actually saying the opposite in the quoted snippet.

UPDATE: As of right now, Skeptical Sports Analysis is the #1 result for these searches as well (no quotation marks, and all have actually been used to find the site):

why was dennis rodman so good at rebounding – Leads to Rodman series, Part 1/4(b). Makes sense, although strictly speaking I’ve never addressed this question.
skynet does not know the rules of football – It’s a direct quote, so obv it leads to Skynet.
nfl predictions using regression analysis – Oddly enough, this also leads to Skynet. I guess technically my neural network is a regression.
how often are sports analysts actually – Leads to main page. Actually what? I don’t know.

Graph of the Day: NBA Player Stats v. Team Differentials (Follow-Up)

In this post from my Rodman series, I speculated that “individual TRB% probably has a more causative effect on team TRB% than individual PPG does on team PPG.” Now, using player/team differential statistics (first deployed in my last Rodman post), I think I can finally test this hypothesis:

^{Note: As before, this dataset includes all regular season NBA games from 1986-2010. For each player who both played and missed at least 20 games in the same season (and averaged at least 20 minutes per game played), differentials are calculated for each team stat with the player in and out of the lineup, weighted by the smaller of games played or games missed that season. The filtered data includes 1341 seasons and a total of 39,162 weighted games.}

This graph compares individual player statistics to his in/out differential for each corresponding team statistic. For example, a player’s points per game is correlated to his team’s points per game with him in the lineup minus their points per game with him out of the lineup. Unlike direct correlations to team statistics, this technique tells us how much a player’s performance for a given metric actually causes his team to be better at the thing that metric measures.

Lower values on this scale can potentially indicate a number of things, particularly two of my favorites: duplicability (stat reflects player “contributions” that could have happened anyway—likely what’s going on with Defensive Rebounding %), and/or entanglement (stat is caused by team performance more than it contributes to team performance—likely what’s going on with Assist %).

In any case, the data definitely appears to support my hypothesis: Player TRB% does seem to have a stronger causative effect on team TRB% than player PPG does on team PPG.

The Case for Dennis Rodman, Part 2/4 (a)(ii)—Player Valuation and Unconventional Wisdom

In my last post in this series, I outlined and criticized the dominance of gross points (specifically, points per game) in the conventional wisdom about player value. Of course, serious observers have recognized this issue for ages, responding in a number of ways—the most widespread still being ad hoc (case by case) analysis. Not satisfied with this approach, many basketball statisticians have developed advanced “All in One” player valuation metrics that can be applied broadly.

In general, Dennis Rodman has not benefitted much from the wave of advanced “One Size Fits All” basketball statistics. Perhaps the most notorious example of this type of metric—easily the most widely disseminated advanced player valuation stat out there—is John Hollinger’s Player Efficiency Rating:

In addition to ranking Rodman as the 7th best player on the 1995-96 Bulls championship team, PER is weighted to make the league average exactly 15—meaning that, according to this stat, Rodman (career PER: 14.6) was actually a below average player. While Rodman does significantly better in a few predictive stats (such as David Berri’s Wages of Wins) that value offensive rebounding very highly, I think that, generally, those who subscribe to the Unconventional Wisdom typically accept one or both of the following: 1) that despite Rodman’s incredible rebounding prowess, he was still just a very good a role-player, and likely provided less utility than those who were more well-rounded, or 2) that, even if Rodman was valuable, a large part of his contribution must have come from qualities that are not typically measurable with available data, such as defensive ability.

My next two posts in this series will put the lie to both of those propositions. In section (b) of Part 2, I will demonstrate Rodman’s overall per-game contributions—not only their extent and where he fits in the NBA’s historical hierarchy, but exactly where they come from. Specifically, contrary to both conventional and unconventional wisdom, I will show that his value doesn’t stem from quasi-mystical unmeasurables, but from exactly where we would expect: extra possessions stemming from extra rebounds. In part 3, I will demonstrate (and put into perspective) the empirical value of those contributions to the bottom line: winning. These two posts are at the heart of The Case for Dennis Rodman, qua “case for Dennis Rodman.”

But first, in line with my broader agenda, I would like to examine where and why so many advanced statistics get this case wrong, particularly Hollinger’s Player Efficiency Rating. I will show how, rather than being a simple outlier, the Rodman data point is emblematic of major errors that are common in conventional unconventional sports analysis – both as a product of designs that disguise rather than replace the problems they were meant to address, and as a product of uncritically defending and promoting an approach that desperately needs reworking.

Player Efficiency Ratings

John Hollinger deserves much respect for bringing advanced basketball analysis to the masses. His Player Efficiency Ratings are available on ESPN.com under Hollinger Player Statistics, where he uses them as the basis for his Value Added (VA) and Expected Wins Added (EWA) stats, and regularly features them in his writing (such as in this article projecting the Miami Heat’s 2010-11 record), as do other ESPN analysts. Basketball Reference includes PER in their “Advanced” statistical tables (present on every player and team page), and also use it to compute player Value Above Average and Value Above Replacement (definitions here).

The formula for PER is extremely complicated, but its core idea is simple: combine everything in a player’s stat-line by rewarding everything good (points, rebounds, assists, blocks, and steals), and punishing everything bad (missed shots, turnovers). The value of particular items are weighted by various league averages—as well as by Hollinger’s intuitions—then the overall result is calculated on a per-minute basis, adjusted for league and team pace, and normalized on a scale averaging 15.

Undoubtedly, PER is deeply flawed. But sometimes apparent “flaws” aren’t really “flaws,” but merely design limitations. For example: PER doesn’t account for defense or “intangibles,” it is calculated without resort to play-by-play data that didn’t exist prior to the last few seasons, and it compares players equally, regardless of position or role. For the most part, I will refrain from criticizing these constraints, instead focusing on a few important ways that it fails or even undermines its own objectives.

Predictivity (and: Introducing Win Differential Analysis)

Though Hollinger uses PER in his “wins added” analysis, its complete lack of any empirical component suggests that it should not be taken seriously as a predictive measure. And indeed, empirical investigation reveals that it is simply not very good at predicting a player’s actual impact:

This bubble-graph is a product of a broader study I’ve been working on that correlates various player statistics to the difference in their team’s per-game performance with them in and out of the line-up. The study’s dataset includes all NBA games back to 1986, and this particular graph is based on the 1300ish seasons in which a player who averaged 20+ minutes per game both missed and played at least 20 games. Win% differential is the difference in the player’s team’s winning percentage with and without him (for the correlation, each data-point is weighted by the smaller of games missed or played. I will have much more to write about nitty-gritty of this technique in separate posts).

So PER appears to do poorly, but how does it compare to other valuation metrics?

SecFor (or “Secret Formula”) is the current iteration of an empirically-based “All in One” metric that I’m developing—but there is no shame in a speculative purely a priori metric losing (even badly) as a predictor to the empirical cutting-edge.

However, as I admitted in the introduction to this series, my statistical interest in Dennis Rodman goes way back. One of the first spreadsheets I ever created was in the early 1990’s, when Rodman still played for San Antonio. I knew Rodman was a sick rebounder, but rarely scored—so naturally I thought: “If only there were a formula that combined all of a player’s statistics into one number that would reflect his total contribution.” So I came up with this crude, speculative, purely a priori equation:

Points + Rebounds + 2*Assists + 1.5*Blocks + 2*Steals – 2*Turnovers.

Unfortunately, this metric (which I called “PRABS”) failed to shed much light on the Rodman problem, so I shelved it. PER shares the same intention and core technique, albeit with many additional layers of complexity. For all of this refinement, however, Hollinger has somehow managed to make a bad metric even worse, getting beaten by my OG PRABS by nearly as much as he is able to beat points per game—the Flat Earth of basketball valuation metrics. So how did this happen?

Minutes

The trend in much of basketball analysis is to rate players by their per-minute or per-possession contributions. This approach does produce interesting and useful information, and they may be especially useful to a coach who is deciding who to give more minutes to, or to a GM who is trying to evaluate which bench player to sign in free agency.

But a player’s contribution to winning is necessarily going to be a function of how much extra “win” he is able to get you per minute and the number of minutes you are able to get from him. Let’s turn again to win differential:

For this graph, I set up a regression using each of the major rate stats, plus minutes played (TS%=true shooting percentage, or one half of average points per shot, including free throws and 3 pointers). If you don’t know what a “normalized coefficient” is, just think of it as a stat for comparing the relative importance of regression elements that come in different shapes and sizes. The sample is the same as above: it only includes players who average 20+ minutes per game.

Unsurprisingly, “minutes per game” is more predictive than any individual rate statistic, including true shooting. Simply multiplying PER by minutes played significantly improves its predictive power, managing to pull it into a dead-heat with PRABS (which obviously wasn’t minute-adjusted to begin with).

I’m hesitant to be too critical of the “per minute” design decision, since it is clearly an intentional element that allows PER to be used for bench or rotational player valuation, but ultimately I think this comes down to telos: So long as PER pretends to be an arbiter of player value—which Hollinger himself relies on for making actual predictions about team performance—then minutes are simply too important to ignore. If you want a way to evaluate part-time players and how they might contribute IF they could take on larger roles, then it is easy enough to create a second metric tailored to that end.

Here’s a similar example from baseball that confounds me: Rate stats are fine for evaluating position players, because nearly all of them are able to get you an entire game if you want—but when it comes to pitching, how often someone can play and the number of innings they can give you is of paramount importance. E.g., at least for starting pitchers, it seems to me that ERA is backwards: rather than calculate runs allowed per inning, why don’t they focus on runs denied per game? Using a benchmark of 4.5, it would be extremely easy to calculate: Innings Pitched/2 – Earned Runs. So, if a pitcher gets you 7 innings and allows 2 runs, their “Earned Runs Denied” (ERD) for the game would be 1.5. I have no pretensions of being a sabermetrician, and I’m sure this kind of stat (and much better) is common in that community, but I see no reason why this kind of statistic isn’t mainstream.

More broadly, I think this minutes SNAFU is reflective of an otherwise reasonable trend in the sports analytical community—to evaluate everything in terms of rates and quality instead of quantity—that is often taken too far. In reality, both may be useful, and the optimal balance in a particular situation is an empirical question that deserves investigation in its own right.

PER Rewards Shooting (and Punishes Not Shooting)

As described by David Berri, PER is well-known to reward inefficient shooting:

“Hollinger argues that each two point field goal made is worth about 1.65 points. A three point field goal made is worth 2.65 points. A missed field goal, though, costs a team 0.72 points. Given these values, with a bit of math we can show that a player will break even on his two point field goal attempts if he hits on 30.4% of these shots. On three pointers the break-even point is 21.4%. If a player exceeds these thresholds, and virtually every NBA player does so with respect to two-point shots, the more he shoots the higher his value in PERs. So a player can be an inefficient scorer and simply inflate his value by taking a large number of shots.”

The consequences of this should be properly understood: Since this feature of PER applies to every shot taken, it is not only the inefficient players who inflate their stats. PER gives a boost to everyone for every shot: Bad players who take bad shots can look merely mediocre, mediocre players who take mediocre shots can look like good players, and good players who take good shots can look like stars. For Dennis Rodman’s case—as someone who took very few shots, good or bad— the necessary converse of this is even more significant: since PER is a comparative statistic (even directly adjusted by league averages), players who don’t take a lot of shots are punished.
Structurally, PER favors shooting—but to what extent? To get a sense of it, let’s plot PER against usage rate:

^{Note: Data includes all player seasons since 1986. Usage % is the percentage of team possessions that end with a shot, free throw attempt, or turnover by the player in question. For most practical purposes, it measures how frequently the player shoots the ball.}

That R-squared value corresponds to a correlation of .628, which might seem high for a component that should be in the denominator. Of course, correlations are tricky, and there are a number of reasons why this relationship could be so strong. For example, the most efficient shooters might take the most shots. Let’s see:

Actually, that trend-line doesn’t quite do it justice: that R-squared value corresponds to a correlation of .11 (even weaker than I would have guessed).

I should note one caveat: The mostly flat relationship between usage and shooting may be skewed, in part, by the fact that better shooters are often required to take worse shots, not just more shots—particularly if they are the shooter of last resort. A player that manages to make a mediocre shot out of a bad situation can increase his team’s chances of winning, just as a player that takes a marginally good shot when a slam dunk is available may be hurting his team’s chances. Presently, no well-known shooting metrics account for this (though I am working on it), but to be perfectly clear for the purposes of this post: neither does PER. The strong correlation between usage rate and PER is unrelated. There is nothing in its structure to suggest this is an intended factor, and there is nothing in its (poor) empirical performance that would suggest it is even unintentionally addressed. In other words, it doesn’t account for complex shooting dynamics either in theory or in practice.

Duplicability and Linearity

PER strongly rewards broad mediocrity, and thus punishes lack of the same. In reality, not every point that a player scores means their team will score one more point, just as not every rebound grabbed means that their team will get one more possession. Conversely—and especially pertinent to Dennis Rodman—not every point that a player doesn’t score actually costs his team a point. What a player gets credit for in his stat line doesn’t necessarily correspond with his actual contribution, because there is always a chance that the good things he played a part in would have happened anyway. This leads to a whole set of issues that I typically file under the term “duplicability.”

A related (but sometimes confused) effect that has been studied extensively by very good basketball analysts is the problem of “diminishing returns” – which can be easily illustrated like this: if you put a team together with 5 players that normally score 25 points each, it doesn’t mean that your team will suddenly start scoring 125 points a game. Conversely—and again pertinent to Rodman—say your team has 5 players that normally score 20 points each, and you replace one of them with somebody that normally only scores 10, that does not mean that your team will suddenly start scoring only 90. Only one player can take a shot at a time, and what matters is whether the player’s lack of scoring hurts his team’s offense or not. The extent of this effect can be measured individually for different basketball statistics, and, indeed, studies have showed wide disparities.

As I will discuss at length in Part 2(c), despite hardly ever scoring, differential stats show that Rodman didn’t hurt his teams offenses at all: even after accounting for extra possessions that Rodman’s teams gained from offensive rebounds, his effect on offensive efficiency was statistically insignificant. In this case (as with Randy Moss), we are fortunate that Rodman had such a tumultuous career: as a result, he missed a significant number of games in a season several times with several different teams—this makes for good indirect data. But, for this post’s purposes, the burning question is: Is there any direct way to tell how likely a player’s statistical contributions were to have actually converted into team results?

This is an extremely difficult and intricate problem (though I am working on it), but it is easy enough to prove at least one way that a metric like PER gets it wrong: it treats all of the different components of player contribution linearly. In other words, one more point is worth one more point, whether it is the 15th point that a player scores or the 25th, and one more rebound is worth one more rebound, whether it is the 8th or the 18th. While this equivalency makes designing an all-in one equation much easier (at least for now, my Secret Formula metric is also linear), it is ultimately just another empirically testable assumption.

I have theorized that one reason Rodman’s PER stats are so low compared to his differential stats is that PER punishes his lack of mediocre scoring, while failing to reward the extremeness of his rebounding. This is based on the hypothesis that certain extreme statistics would be less “duplicable” than mediocre ones. As a result, the difference between a player getting 18 rebounds per game vs. getting 16 per game could be much greater than the difference between them getting 8 vs. getting 6. Or, in other words, the marginal value of rebounds would (hypothetically) be increasing.

Using win percentage differentials, this is a testable theory. Just as we can correlate an individual player’s statistics to the win differentials of his team, we can also correlate hypothetical statistics the same way. So say we want to test a metric like rebounds, except one that has increasing marginal value built in: a simple way to approximate that effect is to make our metric increase exponentially, such as using rebounds squared. If we need even more increasing marginal value, we can try rebounds cubed, etc. And if our metric has several different components (like PER), we can do the same for the individual parts: the beauty is that, at the end of the day, we can test—empirically—which metrics work and which don’t.

For those who don’t immediately grasp the math involved, I’ll go into a little detail: A linear relationship is really just an exponential relationship with an exponent of 1. So let’s consider a toy metric, “PR,” which is calculated as follows: Points + Rebounds. This is a linear equation (exponent = 1) that could be rewritten as follows: (Points)^1 + (Rebounds)^1. However, if, as above, we thought that both points and rebounds should have increasing marginal values, we might want to try a metric (call it “PRsq”) that combined points and rebounds squared, as follows: (Points)^2 + (Rebounds)^2. And so on. Here’s an example table demonstrating the increase in marginal value:

The fact that each different metric leads to vastly different magnitudes of value is irrelevant: for predictive purposes, the total value for each component will be normalized — the relative value is what matters (just as “number of pennies” and “number of quarters” are equally predictive of how much money you have in your pocket). So applying this concept to an even wider range of exponents for several relevant individual player statistics, we can empirically examine just how “exponential” each statistic really is:

For this graph, I looked at each of the major rate metrics (plus points per game) individually. So, for each player-season in my (1986-) sample, I calculated the number of points, points squared, points^3rd. . . points^10th power, and then correlated all of these to that player’s win percentage differential. From those calculations, we can find roughly how much the marginal value for each metric increases, based on what exponent produces the best correlation: The smaller the number at the peak of the curve, the more linear the metric is—the higher the number, the more exponential (i.e., extreme values are that much more important). When I ran this computation, the relative shape of each curve fit my intuitions, but the magnitudes surprised me: That is, many of the metrics turned out to be even more exponential than I would have guessed.

As I know this may be confusing to many of my readers, I need to be absolutely clear: the shape of each curve has nothing to do with the actual importance of each metric. It only tells us how much that particular metric is sensitive to very large values. E.g., the fact that Blocks and Assists peak on the left and sharply decline doesn’t make them more or less important than any of the others, it simply means that having 1 block in your scoreline instead of 0 is relatively just as valuable as having 5 blocks instead of 4. On the other extreme, turnovers peak somewhere off the chart, suggesting that turnover rates matter most when they are extremely high.

For now, I’m not trying to draw a conclusive picture about exactly what exponents would make for an ideal all-in-one equation (polynomial regressions are very very tricky, though I may wade into those difficulties more in future blog posts). But as a minimum outcome, I think the data strongly supports my hypothesis: that many stats—especially rebounds—are exponential predictors. Thus, I mean this less as a criticism of PER than as an explanation of why it undervalues players like Dennis Rodman.

Gross, and Points

In subsection (i), I concluded that “gross points” as a metric for player valuation had two main flaws: gross, and points. Superficially, PER responds to both of these flaws directly: it attempts to correct the “gross” problem both by punishing bad shots, and by adjusting for pace and minutes. It attacks the “points” problem by adding rebounds, assists, blocks, steals, and turnovers. The problem is, these “solutions” don’t match up particularly well with the problems “gross” and “points” present.
The problem with the “grossness” of points certainly wasn’t minutes (note: for historical comparisons, pace adjustments are probably necessary, but the jury is still out on the wisdom of doing the same on a team-by-team basis within a season). The main problem with “gross” was shooting efficiency: If someone takes a bunch of shots, they will eventually score a lot of points. But scoring points is just another thing that players do that may or may not help their teams win. PER attempted to account for this by punishing missed shots, but didn’t go far enough. The original problem with “gross” persists: As discussed above, taking shots helps your rating, whether they are good shots or not.

As for “points”: in addition to any problems created by having arbitrary (non-empirical) and linear coefficients, the strong bias towards shooting causes PER to undermine its key innovation—the incorporation of non-point components. This “bias” can be represented visually:

^{Note: This data comes from a regression to PER including each of the rate stats corresponding to the various components of PER.}

This pie chart is based on a linear regression including rate stats for each of PER’s components. Strictly, what it tells us is the relative value of each factor to predicting PER if each of the other factors were known. Thus, the “usage” section of this pie represents the advantage gained by taking more shots—even if all your other rate stats were fixed. Or, in other words, pure bias (note that the number of shots a player takes is almost as predictive as his shooting ability).

For fun, let’s compare that pie to the exact same regression run on Points Per Game rather than PER:

^{Note: These would not be the best variables to select if you were actually trying to predict a player’s Points Per Game. Note also that “Usage” in these charts is NOT like “Other”—while other variables may affect PPG, and/or may affect the items in this regression, they are not represented in these charts.}

Interestingly, Points Per Game was already somewhat predictable by shooting ability, turnovers, defensive rebounding, and assists. While I hesitate to draw conclusions from the aesthetic comparison, we can guess why perhaps PER doesn’t beat PPG as significantly as we might expect: it appears to share much of the same DNA. (My more wild and ambitious thoughts suspect that these similarities reflect the strength of our broader pro-points bias: even when designing an All-in-One statistic, even Hollinger’s linear, non-empirical, a priori coefficients still mostly reflect the conventional wisdom about the importance of many of the factors, as reflected in the way that they relate directly to points per game).

I could make a similar pie-chart for Win% differential, but I think it might give the wrong impression: these aren’t even close to the best set of variables to use for that purpose. Suffice it to say that it would look very, very different (for an imperfect picture of how much so, you can compare to the values in the Relative Importance chart above).

Conclusions

The deeper irony with PER is not just that it could theoretically be better, but that it adds many levels of complexity to the problem it purports to address, ultimately failing in strikingly similar ways. It has been dressed up around the edges with various adjustments for team and league pace, incorporation of league averages to weight rebounds and value of possession, etc. This is, to coin a phrase, like putting lipstick on a pig. The energy that Hollinger has spent on dressing up his model could have been better spent rethinking the core of it.

In my estimation, this pattern persists among many extremely smart people who generate innovative models and ideas: once created, they spend most of their time—entire careers even—in order: 1) defending it, 2) applying it to new situations, and 3) tweaking it. This happens in just about every field: hard and soft sciences, economics, history, philosophy, even literature. Give me an academic who creates an interesting and meaningful model, and then immediately devotes their best efforts to tearing it apart! In all my education, I have had perhaps two professors who embraced this approach, and I would rank both among my very favorites.

This post and the last were admittedly relatively light on Rodman-specific analysis, but that will change with a vengeance in the next two. Stay tuned.

Update (5/13/11): Commenter “Yariv” correctly points out that an “exponential” curve is technically one in the form y^x (such as 2^x, 3^x, etc), where the increasing marginal value I’m referring to in the “Linearity” section above is about terms in the form x^y (e.g., x^2, x^3, etc), or monomial terms with an exponent not equal to 1. I apologize for any confusion, and I’ll rewrite the section when I have time.

The Aesthetic Case Against 18 Games

By most accounts, the NFL’s plan to expand the regular season from 16 to 18 games is a done deal. Indulge me for a moment as I take off my Bill-James-Wannabe cap and put on my dusty old Aristotle-Wannabe kausia: In addition to various practical drawbacks, moving to 18 games risks disturbing the aesthetic harmony—grounded in powerful mathematics—inherent in the 16 game season.
Analytically, it is easy to appreciate the convenience of having the season break down cleanly into 8-game halves and 4-game quarters. Powers of 2 like this are useful and aesthetically attractive: after all, we are symmetrical creatures who appreciate divisibility. But we have a possibly even more powerful aesthetic attachment to certain types of asymmetrical relationships: Mozart’s piano concertos aren’t divided into equally-sized beginnings, middles and ends. Rather, they are broken into exposition, development, and recapitulation—each progressively shorter than the last.

Similarly, the 16 game season can fairly cleanly be broken into 3 or 4 progressively shorter but more important sections. Using roughly the same proportions that Mozart would, the first 10 games (“exposition”) would set the stage and reveal who we should be paying attention to; the next 3-4 games (“development”) would be where the race for playoff positioning really begins in earnest, and the final 2-3 weeks (“recapitulation”) are where hopes are realized and hearts are broken—including the final weekend when post-season fates are settled. Now, let’s represent the season as a rectangle with sides 16 (length of the season) and 10 (length of the “exposition”), broken down into consecutively smaller squares representing each section:

^{Note: The “last” game gets the leftover space, though if the season were longer we could obviously keep going.}

At this point many of you probably know where this is going: The ratio between each square to all of the smaller pieces is roughly equal, corresponding to the “divine proportion,” which is practically ubiquitous in classical music, as well as in everything from book and movie plots to art and architecture to fractal geometry to unifying theories of “all animate and inanimate systems.” Here it is again (incredibly clumsily-sketched) in the more recognizable spiral form:

The golden ratio is represented in mathematics by the irrational constant phi, which is:

1.6180339887…

Which, when divided into 1 gets you:

.6180339887…

Beautiful, right? So the roughly 10/4/1/1 breakdown above is really just 16 multiplied by 1/phi, with the remainder multiplied by 1/phi, etc—9.9, 3.8, 1.4, .9—rounded to the nearest game. Whether this corresponds to your thinking about the relative significance of each portion of the season is admittedly subjective. But this is an inescapably powerful force in aesthetics (along with symmetricality and symbols of virility and fertility), and can be found in places most people would never suspect, including in professional sports. Let’s consider some anecdotal supporting evidence:

The length of a Major League Baseball season is 162 games. Not 160, but 162. That should look familiar.
Both NBA basketball and NHL hockey have 82-game seasons, or roughly half-phi. Note 81 games would be impractical, because of need for equal number of home and road games (but bonus points if you’ve ever felt like the NBA season was exactly 1 game too long).
The “exposition” portion of a half-phi season would be 50 games. The NHL and NBA All-Star breaks both take place right around game 50, or a little later, each year.
Though still solidly in between 1/2 and 2/3 of the way through the season, MLB’s “Summer Classic” usually takes place slightly earlier, around game 90 (though I might submit that the postseason crunch doesn’t really start until after teams build a post-All Star record for people to talk about).
The NFL bye weeks typically end after week 10.
Fans and even professional sports analysts are typically inclined to value “clutch” players—i.e., those who make their bones in the “Last” quadrant above—way more than a non-aesthetic analytical approach would warrant.

Etc.
So fine, say you accept this argument about how people observe sports, your next question may be: well, what’s wrong with 18 games? any number of games can be divided into phi-sized quadrants, right? Well, the answer is basically yes, it can, but it’s not pretty:

The numbers 162, 82, and 16 all share a couple of nice qualities: first they are all roughly divisible by 4, so you have nice clean quarter-seasons. Second, they each have aesthetically pleasing “exposition” periods: 100 games in MLB, 50 in the NBA and NHL, and 10 in the NFL. The “exposition” period in an 18-game season would be 11 games. Yuck! These season-lengths balance our competing aesthetic desires for the harmony of symmetry and excitement of asymmetry. We like our numbers round, but not too round. We want them dynamic, but workable.

Finally, as to why the NFL should care about vague aesthetic concerns that it takes a mathematician to identify, I can only say: I don’t think these patterns would be so pervasive in science, art, and in broader culture if they weren’t really important to us, whether we know it or not. Human beings are symmetrical down the middle, but as some guy in Italy noticed, golden rectangles are not only woven into our design, but into the design of the things we love. Please, NFL, don’t take that away from us.

C.R.E.A.M. (Or, “How to Win a Championship in Any Sport”)

Does cash rule everything in professional sports? Obviously it keeps the lights on, and it keeps the best athletes in fine bling, but what effect does the root of all evil have on the competitive bottom line—i.e., winning championships?

For this article, let’s consider “economically predictable” a synonym for “Cash Rules”: I will use extremely basic economic reasoning and just two variables—presence of a salary cap and presence of a salary max in a sport’s labor agreement—to establish, ex ante, which fiscal strategies we should expect to be the most successful. For each of the 3 major sports, I will then suggest (somewhat) testable hypotheses, and attempt to examine them. If the hypotheses are confirmed, then Method Man is probably right—dollar dollar bill, etc.

Conveniently, on a basic yes/no grid of these two variables, our 3 major sports in the U.S. fall into 3 different categories:

So before treating those as anything but arbitrary arrangements of 3 letters, we should consider the dynamics each of these rules creates independently. If your sport has a team salary cap, getting “bang for your buck” and ferreting out bargains is probably more important to winning than overall spending power. And if your sport has a low maximum individual salary, your ability to obtain the best possible players—in a market where everyone knows their value but must offer the same amount—will also be crucial. Considering permutations of thriftiness and non-economic acquisition ability, we end up with a simple ex ante strategy matrix that looks like this:

These one-word commandments may seem overly simple—and I will try to resolve any ambiguity looking at the individual sports below—but they are only meant to describe the most basic and obvious economic incentives that salary caps and salary maximums should be expected to create in competitive environments.

Major League Baseball: Spend

Hypothesis: With free-agency, salary arbitration, and virtually no payroll restrictions, there is no strategic downside to spending extra money. Combined with huge economic disparities between organizations, this means that teams that spend the most will win the most.

Analysis: Let’s start with the New York Yankees (shocker!), who have been dominating baseball since 1920, when they got Babe Ruth from the Red Sox for straight cash, homey. Note that I take no position on whether the Yankees filthy lucre is destroying the sport of Baseball, etc. Also, I know very little about the Yankees payroll history, prior to 1988 (the earliest the USA Today database goes). But I did come across this article from several years ago, which looks back as far as 1977. For a few reasons, I think the author understates the case. First, the Yankees low-salary period came at the tail end of a 12 year playoff drought (I don’t have the older data to manipulate, but I took the liberty to doodle on his original graph):

^{Note: Smiley-faces are Championship seasons. The question mark is for the 1994 season, which had no playoffs.}

Also, as a quirk that I’ve discussed previously, I think including the Yankees in the sample from which the standard deviation is drawn can be misleading: they have frequently been such a massive outlier that they’ve set their own curve. Comparing the Yankees to the rest of the league, from last season back to 1988, looks like this:

^{Note: Green are Championship seasons. Red are missed playoffs.}

In 2005 the rest-of-league average payroll was ~$68 million, and the Yankees’ was ~$208 million (the rest-of-league standard deviation was $23m, but including the Yankees, it would jump to $34m).

While they failed to win the World Series in some of their most expensive seasons, don’t let that distract you: money can’t guarantee a championship, but it definitely improves your chances. The Yankees have won roughly a quarter of the championships over the last 20 years (which is, astonishingly, below their average since the Ruth deal). But it’s not just them. Many teams have dramatically increased their payrolls in order to compete for a World Series title—and succeeded! Over the past 22 years, the top 3 payrolls (per season) have won a majority of titles:

As they make up only 10% of the league, this means that the most spendy teams improved their title chances, on average, by almost a factor of 6.

National Basketball Association: Recruit (Or: “Press Your Bet”)

Hypothesis: A fairly strict salary cap reigns in spending, but equally strict salary regulations mean many teams will enjoy massive surplus value by paying super-elite players “only” the max. Teams that acquire multiple such players will enjoy a major championship advantage.

Analysis: First, in case you were thinking that the 57% in the graph above might be caused by something other than fiscal policy, let’s quickly observe how the salary cap kills the “spend” strategy:

Payroll information from USA Today’s NBA and NFL Salary Databases (incidentally, this symmetry is being threatened, as the Lakers, Magic, and Mavericks have the top payrolls this season).

I will grant there is a certain apples-to-oranges comparison going on here: the NFL and NBA salary-cap rules are complex and allow for many distortions. In the NFL teams can “clump” their payroll by using pro-rated signing bonuses (essentially sacrificing future opportunities to exceed the cap in the present), and in the NBA giant contracts are frequently moved to bad teams that want to rebuild, etc. But still: 5%. Below expectation if championships were handed out randomly.
And basketball championships are NOT handed out randomly. My hypothesis predicts that championship success will be determined by who gets the most windfall value from their star player(s). Fifteen of the last 20 NBA championships have been won by Kobe Bryant, Tim Duncan, or Michael Jordan. Clearly star-power matters in the NBA, but what role does salary play in this?

Prior to 1999, the NBA had no salary maximum, though salaries were regulated and limited in a variety of ways. Teams had extreme advantages signing their own players (such as Bird rights), but lack of competition in the salary market mostly kept payrolls manageable. Michael Jordan famously signed a lengthy $25 million contract extension basically just before star player salaries exploded, leaving the Bulls with the best player in the game for a song (note: Hakeem Olajuwon’s $55 million payday came after he won 2 championships as well). By the time the Bulls were forced to pay Jordan his true value, they had already won 4 championships and built a team around him that included 2 other All-NBA caliber players (including one who also provided extreme surplus value). Perhaps not coincidentally, year 6 in the graph below is their record-setting 72-10 season:

^{Note: Michael Jordan’s salary info found here. Historical NBA salary cap found here.}

The star player salary situation caught the NBA off-guard. Here’s a story from Time magazine in 1996 that quotes league officials and executives:

“It’s a dramatic, strategic judgment by a few teams,” says N.B.A. deputy commissioner Russ Granik. .
Says one N.B.A. executive: “They’re going to end up with two players making about two-thirds of the salary cap, and another pair will make about 20%. So that means the rest of the players will be minimum-salary players that you just sign because no one else wants them.” . . .
Granik frets that the new salary structure will erode morale. “If it becomes something that was done across the league, I don’t think it would be good for the sport,” he says.

What these NBA insiders are explaining is basic economics: Surprise! Paying better players big money means less money for the other guys. Among other factors, this led to 2 lockouts and the prototype that would eventually lead to the current CBA (for more information than you could ever want about the NBA salary cap, here is an amazing FAQ).

The fact that the best players in the NBA are now being underpaid relative to their value is certain. As a back of the envelope calculation: There are 5 players each year that are All-NBA 1st team, while 30+ players each season are paid roughly the maximum. So how valuable are All-NBA 1st team players compared to the rest? Let’s start with: How likely is an NBA team to win a championship without one?

In the past 20 seasons, only the 2003-2004 Detroit Pistons won the prize without a player who was a 1st-Team All-NBAer in their championship year.
To some extent, these findings are hard to apply strategically. All but those same Pistons had at least one home-grown All-NBA (1st-3rd team) talent—to win, you basically need the good fortune to catch a superstar in the draft. If there is an actionable take-home, however, it is that most (12/20) championship teams have also included a second All-NBA talent acquired through trade or free agency: the Rockets won after adding Clyde Drexler, the second Bulls 3-peat added Dennis Rodman (All-NBA 3rd team with both the Pistons and the Spurs), the Lakers and Heat won after adding Shaq, the Celtics won with Kevin Garnett, and the Lakers won again after adding Pau Gasol.

Each of these players was/is worth more than their market value, in most cases as a result of the league’s maximum salary constraints. Also, in most of these cases, the value of the addition was well-known to the league, but the inability of teams to outbid each other meant that basketball money was not the determinant factor in the players choosing their respective teams. My “Recruit” strategy anticipated this – though it perhaps understates the relative importance of your best player being the very best. This is more a failure of the “recruit” label than of the ex ante economic intuition, the whole point of which was that cap+max –> massive importance of star players.

National Football League: Economize (Or: “WWBBD?”)

Hypothesis: The NFL’s strict salary cap and lack of contract restrictions should nullify both spending and recruiting strategies. With elite players paid closer to what they are worth, surplus value is harder to identify. We should expect the most successful franchises to demonstrate both cunning and wise fiscal policy.

Analysis: Having a cap and no max salaries is the most economically efficient fiscal design of any of the 3 major sports. Thus, we should expect that massively dominating strategies to be much harder to identify. Indeed, the dominant strategies in the other sports are seemingly ineffective in the NFL: as demonstrated above, there seems to be little or no advantage to spending the most, and the abundant variance in year-to-year team success in the NFL would seem to rule out the kind of individual dominance seen in basketball.

Thus, to investigate whether cunning and fiscal sense are predominant factors, we should imagine what kinds of decisions a coach or GM would make if his primary qualities were cunning and fiscal sensibility. In that spirit, I’ve come up with a short list of 5 strategies that I think are more or less sound, and that are based largely on classically “economic” considerations:

1. Beg, borrow, or steal yourself a great quarterback:
Superstar quarterbacks are probably underpaid—even with their monster contracts—thus making them a good potential source for surplus value. Compare this:

Note: WPA (wins added) stats from here.

With this:

The obvious caveat here is that the entanglement question is still empirically open: How much do good QB’s make their teams win v. How much do winning teams make their QB’s look good? But really quarterbacks only need to be responsible for a fraction of the wins reflected in their stats to be worth more than what they are being paid. (An interesting converse, however, is this: the fact that great QB’s don’t win championships with the same regularity as, say, great NBA players, suggests that a fairly large portion of the “value” reflected by their statistics is not their responsibility).

2. Plug your holes with the veteran free agents that nobody wants, not the ones that everybody wants:
If a popular free agent intends to go to the team that offers him the best salary, his market will act substantially like a “common value” auction. Thus, beware the Winner’s Curse. In simple terms: If 1) a player’s value is unknown, 2) each team offers what they think the player is worth, and 3) each team is equally likely to be right; then: 1) The player’s expected value will correlate with the average bid, and 2) the “winning” bid probably overpaid.

Moreover, even if the winner’s bid is exactly right, that just means they will have successfully gained nothing from the transaction. Assuming equivalent payrolls, the team with the most value (greatest chance of winning the championship) won’t be the one that pays the most correct amount for its players, it will—necessarily—be the one that pays the least per unit of value. To accomplish this goal, you should avoid common value auctions as much as possible! In free agency, look for the players with very small and inefficient markets (for which #3 above is least likely to be true), and then pay them as little as you can get away with.

3. Treat your beloved veterans with cold indifference.
If a player is beloved, they will expect to be paid. If they are not especially valuable, they will expect to be paid anyway, and if they are valuable, they are unlikely to settle for less than they are worth. If winning is more important to you than short-term fan approval, you should be both willing and prepared to let your most beloved players go the moment they are no longer a good bargain.

4. Stock up on mid-round draft picks.
Given the high cost of signing 1st round draft picks, 2nd round draft picks may actually be more valuable. Here is the crucial graph from the Massey-Thaler study of draft pick value (via Advanced NFL Stats):

The implications of this outcome are severe. All else being equal, if someone offers you an early 2nd round draft pick for your early 1st round draft pick, they should be demanding compensation from you (of course, marginally valuable players have diminishing marginal value, because you can only have/play so many of them at a time).

5. When the price is right: Gamble.

This rule applies to fiscal decisions, just as it does to in-game ones. NFL teams are notoriously risk-averse in a number of areas: they are afraid that someone after one down season is washed up, or that an outspoken player will ‘disrupt’ the locker room, or that a draft pick might have ‘character issues’. These sorts of questions regularly lead to lengthy draft slides and dried-up free agent markets. And teams are right to be concerned: these are valid possibilities that increase uncertainty. Of course, there are other possibilities. Your free agent target simply may not be as good as you hope they are, or your draft pick may simply bust out. Compare to late-game 4th-down decisions: Sometimes going for it on 4th down will cause you to lose immediately and face a maelstrom of criticism from fans and press, where punting or kicking may quietly lead to losing more often. Similarly, when a team takes a high-profile personnel gamble and it fails, they may face a maelstrom of criticism from fans and press, where the less controversial choice might quietly lead to more failure.

The economizing strategy here is to favor risks when they are low cost but have high upsides. In other words, don’t risk a huge chunk of your cap space on an uncertain free agent prospect, risk a tiny chunk of your cap space on an even more uncertain prospect that could work out like gangbusters.

Evaluation:

Now, if only there were a team and coach dedicated to these principles—or at least, for contrapositive’s sake, a team that seemed to embrace the opposite.

Oh wait, we have both! In the last decade, Bill Belichick and the New England Patriots have practically embodied these principles, and in the process they’ve won 3 championships, have another 16-0/18-1 season, have set the overall NFL win-streak records, and are presently the #1 overall seed in this year’s playoffs. OTOH, the Redskins have practically embodied the opposite, and they have… um… not.
Note that the Patriots’ success has come despite a league fiscal system that allows teams to “load up” on individual seasons, distributing the cost onto future years (which, again, helps explain the extreme regression effect present in the NFL). Considering the long odds of winning a Super Bowl—even with a solid contender—this seems like an unwise long-run strategy, and the most successful team of this era has cleverly taken the long view throughout.

Conclusions

The evidence in MLB and in the NBA is ironclad: Basic economic reasoning is extremely probative when predicting the underlying dynamics behind winning titles. Over the last 20 years of pro baseball, the top 3 spenders in the league each year win 57% of the championships. Over a similar period in basketball, the 5 (or fewer) teams with 1st-Team All-NBA players have won 95%.

In the NFL, the evidence is more nuance and anecdote than absolute proof. However, our ex ante musing does successfully predict that neither excessive spending nor recruiting star players at any cost (excepting possibly quarterbacks) is a dominant strategy.

On balance, I would say that the C.R.E.A.M. hypothesis is substantially more supported by the data than I would have guessed.