Tim Tebow and the Taxonomy of Clutch

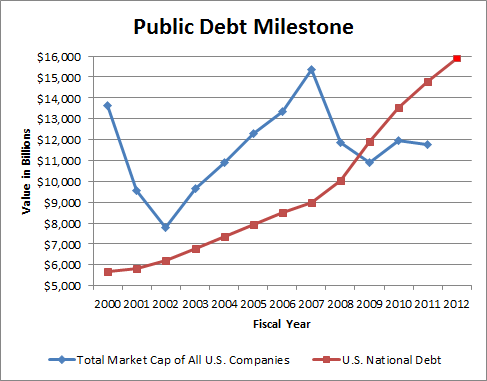
There’s nothing people love more in sports than the appearance of “clutch”ness, probably because the ability to play “up” to a situation implies a sort of super-humanity, and we love our super-heroes. Prior to this last weekend, Tim Tebow had a remarkable streak of games in which he (and his team) played significantly better in crucial 4th-quarter situations than he (or they) did throughout the rest of those contests. Combined with Tebow’s high profile, his extremely public religious conviction, and a “divine intervention” narrative that practically wrote itself, this led to a perfect storm of hype. With the din of that hype dying down a bit (thank you, Bill Belichick), I thought I’d take the chance to explore a few of my thoughts on “clutchness” in general.

This may be a bit of a surprise coming from a statistically-oriented self-professed skeptic, but I’m a complete believer in “clutch.”  In this case, my skepticism is aimed more at those who deny clutch out of hand: The principle that “Clutch does not exist” is treated as something of a sacred tenet by many adherents of the Unconventional Wisdom.

On the other hand, my belief in Clutch doesn’t necessarily mean I believe in mystical athletic superpowers. Rather, I think the “clutch” effect—that is, scenarios where the performance of some teams/players genuinely improves when game outcomes are in the balance—is perfectly rational and empirically supported.  Indeed, the simple fact that winning is a statistically significant predictive variable on top of points scored and points allowed—demonstrably true for each of the 3 major American sports—is very nearly proof enough.

The differences between my views and those of clutch-deniers are sometimes more semantic and sometimes more empirical.  In its broadest sense, I would describe “clutch” as a property inherent in players/teams/coaches who systematically perform better than normal in more important situations. From there, I see two major factors that divide clutch into a number of different types: 1) Whether or not the difference is a product of the individual or team’s own skill, and 2) whether their performance in these important spots is abnormally good relative to their performance (in less important spots), whether it is good relative to the typical performance in those spots, or both.  In the following chart, I’ve listed the most common types of Clutch that I can think of, a couple of examples of each, and how I think they break down w/r/t those factors (click to enlarge):

Here are a few thoughts on each:

1. Reverse Clutch

I first discussed the concept of “reverse clutch” in this post in my Dennis Rodman series.  Put simply, it’s a situation where someone has clutch-like performance by virtue of playing badly in less important situations.

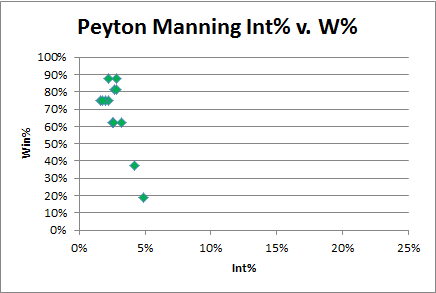
While I don’t think this is a particularly common phenomenon, it may be relevant to the Tebow discussion.  During Sunday’s Broncos/Pats game, I tweeted that at least one commentator seemed to be flirting with the idea that maybe Tebow would be better off throwing more interceptions. Noting that, for all of Tebow’s statistical shortcomings, his interception rate is ridiculously low, and then noting that Tebow’s “ugly” passes generally err on the ultra-cautious side, the commentator seemed poised to put the two together—if just for a moment—before his partner steered him back to the mass media-approved narrative.

If you’re not willing to take the risks that sometimes lead to interceptions, you may also have a harder time completing passes, throwing touchdowns, and doing all those things that quarterbacks normally do to win games.  And, for the most part, we know that Tebow is almost religiously (pun intended) committed to avoiding turnovers.  However, in situations where your team is trailing in the 4th quarter, you may have no choice but to let loose and take those risks.  Thus, it is possible that a Tim Tebow who takes risks more optimally is actually a significantly better quarterback than the Q1-Q3 version we’ve seen so far this season, and the 4th quarter pressure situations he has faced have simply brought that out of him.

That may sound farfetched, and I certainly wouldn’t bet my life on it, but it also wouldn’t be unprecedented.  Though perhaps a less extreme example, early in his career Ben Roethlisburger played on a Pittsburgh team that relied mostly on its defense, and was almost painfully conservative in the passing game.  He won a ton, but with superficially unimpressive stats, a fairly low interception rate, and loads of “clutch” performances. His rookie season he passed for only 187 yards a game, yet had SIX 4th quarter comebacks.  Obviously, he eventually became regarded as an elite QB, with statistics to match.

 2. Not Choking

A lot of professional athletes are *not* clutch, or, more specifically, are anti-clutch. See, e.g., professional kickers.  They succumb under pressure, just as any non-professionals might. While most professionals probably have a much greater capacity for handling pressure situations than amateurs, there are still significant relative imbalances between them.  The athletes who do NOT choke under pressure are thus, by comparison, clutch.

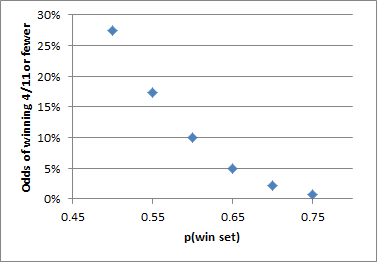
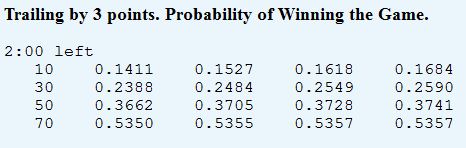
Some athletes may be more “mentally tough” than others.  I love Roger Federer, and think he is among the top two tennis player of all time (Bjorn Borg being the other), and in many ways I even think he is under-appreciated despite all of his accolades.  Yet, he has a pretty crap record in the closest matches, especially late in majors: lifetime, he is 4-7 in 5 set matches in the Quarterfinals or later, including a 2-4 record in his last 6.  For comparison, Nadal is 4-1 in similar situations (2-1 against Federer), and Borg won 5-setters at an 86% clip.

Extremely small sample, sure. But compared to Federer’s normal expectation on a set by set basis over the time-frame (even against tougher competition), the binomial probability of him losing that much without significantly diminished 5th set performance is extremely low:

Thus, as a Bayesian matter, it’s likely that a portion of Rafael Nadal’s apparent “clutchness” can be attributed to Roger Federer.

3. Reputational Clutch.

In the finale to my Rodman series, I discussed a fictional player named “Bjordson,” who is my amalgamation of Michael Jordan, Larry Bird, and Magic Johnson, and I noted that this player has a slightly higher Win % differential than Rodman.

Now, I could do a whole separate post (if not a whole separate series) on the issue, but it’s interesting that Bjordson also has an extremely high X-Factor: that is, the average difference between their actual Win % differential and the Win % differential that would be predicted by their Margin of Victory differential is, like Rodman’s, around 10% (around 22.5% vs. 12.5%).  [Note: Though the X-Factors are similar, this is subjectively a bit less surprising than Rodman having such a high W% diff., mostly because I started with W% diff. this time, so some regression to the mean was expected, while in Rodman’s case I started with MOV, so a massively higher W% was a shocker.  But regardless, both results are abnormally high.]

Now, I’m sure that the vast majority of sports fans presented with this fact would probably just shrug and accept that Jordan, Bird and Johnson must have all been uber-clutch, but I doubt it.  Systematically performing super-humanly better than you are normally capable of is extremely difficult, but systematically performing worse than you are normally capable of is pretty easy.  Rodman’s high X-Factor was relatively easy to understand (as Reverse Clutch), but these are a little trickier.

Call it speculation, but I suspect that a major reason for this apparent clutchiness is that being a super-duper-star has its privileges. E.g.:

In other words, ref bias may help super-stars win even more than their super-skills would dictate.

I put Tim Tebow in the chart above as perhaps having a bit of “reputational clutch” as well, though not because of officiating.  Mostly it just seemed that, over the last few weeks, the Tebow media frenzy led to an environment where practically everyone on the field was going out of their minds—one way or the other—any time a game got close late.

4. Skills Relevant to Endgame

Numbers 4 and 5 in the chart above are pretty closely related.  The main distinction is that #4 can be role-based and doesn’t necessarily imply any particular advantage.  In fact, you could have a relatively poor player overall who, by virtue of their specific skillset, becomes significantly more valuable in endgame situations.  E.g., closing pitchers in baseball: someone with a comparatively high ERA might still be a good “closing” option if they throw a high percentage of strikeouts (it doesn’t matter how many home runs you normally give up if a single or even a pop-up will lose the game).

Straddling 4 and 5 is one of the most notorious “clutch” athletes of all time: Reggie Miller.  Many years ago, I read an article that examined Reggie’s career and determined that he wasn’t clutch because he hit an relatively normal percentage of 3 point shots in clutch situations. I didn’t even think about it at the time, but I wish I could find the article now, because, if true, it almost certainly proves exactly the opposite of what the authors intended.

The amazing thing about Miller is that his jump shot was so ugly. My theory is that the sheer bizarreness of his shooting motion made his shot extremely hard to defend (think Hideo Nomo in his rookie year).  While this didn’t necessarily make him a great shooter under normal circumstances, he could suddenly become extremely valuable in any situations where there is no time to set up a shot and heavy perimeter defense is a given. Being able to hit ANY shots under those conditions is a “clutch” skill.

 5. Tactical Superiority (and other endgame skills)

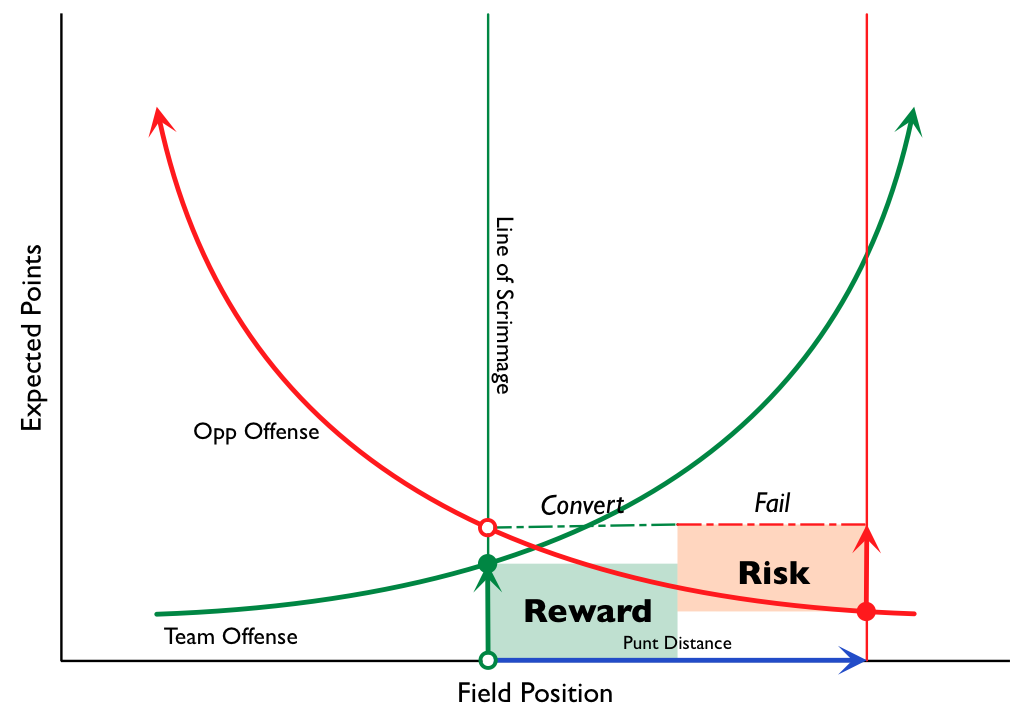
Though other types of skills can fit into this branch of the tree, I think endgame tactics is the area where teams, coaches, and players are most likely to have disparate impacts, thus leading to significant advantages w/r/t winning.  The simple fact is that endgames are very different from the rest of games, and require a whole different mindset. Meanwhile, leagues select for people with a wide variety of skills, leaving some much better at end-game tactics than others.

Win expectation supplants point expectation.  If you’re behind, you have to take more risks, and if you’re ahead, you have to avoid risks—even at the cost of expected value.  If you’re a QB, you need to consider the whole range of outcomes of a play more than just the average outcome or the typical outcome.  If you’re a QB who is losing, you need to throw pride out the window and throw interceptions! There is clock management, knowing when to stay in bounds and when to go down.  As a baseball manager, you may face your most difficult pitching decisions, and as a pitcher, you may have to make unusual pitch decisions.  A batter may have to adjust his style to the situation, and a pitcher needs to anticipate those adjustments.  Etc., etc., ad infinitum.  They may not be as flashy as Reggie Miller 3-ball, but these little things add up, and are probably the most significant source of Clutchness in sports.

6. Conditioning

I listed this separately (rather than as an example of 4 or 5) just because I think it’s not as simple and neat as it seems.

While conditioning and fitness are important in every sport, and they tend to be more important later in games, they’re almost too pervasive to be “clutch” as I described it above.  The fact that most major team sports have more or less uniform game lengths means that conditioning issue should manifest similarly basically every night, and should therefore be reflected in most conventional statistics (like minutes played, margin of victory, etc), not just in those directly related to winning.

Ultimately, I think conditioning has the greatest impact on “clutchness” in Tennis, where it is often the deciding factor in close matches

7. True Clutch.

And finally, we get to the Holy Grail of Clutch.  This is probably what most “skeptics” are thinking of when they deny the existence of Clutch, though I think that such denials—even with this more limited scope—are generally overstated.  If such a quality exists, it is obviously going to be extremely rare, so the various statistical studies that fail to find it prove very little.

The most likely example in mainstream sports would seem to be pre-scandal Tiger Woods.  In his prime, he had an advantage over the field in nearly every aspect of the game, but golf is a fairly high variance sport, and his scoring average was still only a point or two lower than the competition.  Yet his Sunday prowess is well documented: He has gone 48-4 in PGA tournaments when entering the final round with at least a share of the lead, including an 11-1 record with only a share of the lead.  Also, to go a bit more esoteric, Woods has successfully defended a title 22 times.  So, considering he has 71 career wins, and at least 22 of them had to be first timers, that means his title defense record is closer to 40-45%, depending on how often he won titles many times in a row.  Compare this to his overall win-rate of 27%, and the idea that he was able to elevate his game when it mattered to him the most is even more plausible.

Of course, I still contend that the most clutch thing I have ever seen is Packattack’s final jump onto the .1 wire in his legendary A11 run.  Tim Tebow, eat your heart out!

A Defense of Sudden Death Playoffs in Baseball

So despite my general antipathy toward America’s pastime, I’ve been looking into baseball a lot lately.  I’m working on a three part series that will “take on” Pythagorean Expectation.  But considering the sanctity of that metric, I’m taking my time to get it right.

For now, the big news is that Major League Baseball is finally going to have realignment, which will most likely lead to an extra playoff team, and a one game Wild Card series between the non–division winners.  I’m not normally one who tries to comment on current events in sports (though, out of pure frustration, I almost fired up WordPress today just to take shots at Tim Tebow—even with nothing original to say), but this issue has sort of a counter-intuitive angle to it that motivated me to dig a bit deeper.

Conventional wisdom on the one game playoff is pretty much that it’s, well, super crazy.  E.g., here’s Jayson Stark’s take at ESPN:

But now that the alternative to finishing first is a ONE-GAME playoff? Heck, you’d rather have an appendectomy than walk that tightrope. Wouldn’t you?

Though I think he actually likes the idea, precisely because of the loco factor:

So a one-game, October Madness survivor game is what we’re going to get. You should set your DVRs for that insanity right now.

In the meantime, we all know what the potential downside is to this format. Having your entire season come down to one game isn’t fair. Period.

I wouldn’t be too sure about that.  What is fair?  As I’ve noted, MLB playoffs are basically a crapshoot anyway.  In my view, any move that MLB can make toward having the more accomplished team win more often is a positive step.  And, as crazy as it sounds, that is likely exactly what a one game playoff will do.

The reason is simple: home field advantage.  While smaller than in other sports, the home team in baseball still wins around 55% of the time, and more games means a smaller percentage of your series games played at home.  While longer series’ eventually lead to better teams winning more often, the margins in baseball are so small that it takes a significant edge for a team to prefer to play ANY road games:

Note: I calculated these probabilities using my favorite binom.dist function in Excel. Specifically, where the number of games needed to win a series is k, this is the sum from x=0 to x=k of the p(winning x home games) times p(winning at least k-x road games).

So assuming each team is about as good as their records (which, regardless of the accuracy of the assumption, is how they deserve to be treated), a team needs about a 5.75% generic advantage (around 9-10 games) to prefer even a seven game series to a single home game.

But what about the incredible injustice that could occur when a really good team is forced to play some scrub?  E.g., Stark continues:

It’s a lock that one of these years, a 98-win wild-card team is going to lose to an 86-win wild-card team. And that will really, really seem like a miscarriage of baseball justice. You’ll need a Richter Scale handy to listen to talk radio if that happens.

But you know what the answer to those complaints will be?

“You should have finished first. Then you wouldn’t have gotten yourself into that mess.”

Stark posits a 12 game edge between two wild card teams, and indeed, this could lead to a slightly worse spot for the better team than a longer series.  12 games corresponds to a 7.4% generic advantage, which means a 7-game series would improve the team’s chances by about 1% (oh, the humanity!).  But the alternative almost certainly wouldn’t be seven games anyway, considering the first round of the playoffs is already only five.  At that length, the “miscarriage of baseball justice” would be about 0.1% (and vs. 3 games, sudden death is still preferable).

If anything, consider the implications of the massive gap on the left side of the graph above: If anyone is getting screwed by the new setup, it’s not the team with the better record, it’s a better team with a worse record, who won’t get as good a chance to demonstrate their actual superiority (though that team’s chances are still around 50% better than they would have been under the current system).  And those are the teams that really did “[get themselves] into that mess.”

Also, the scenario Stark posits is extremely unlikely: basically, the difference between 4th and 5th place is never 12 games.  For comparison, this season the difference between the best record in the NL and the Wild Card Loser was only 13 games, and in the AL it was only seven.  Over the past ten seasons, each Wild Card team and their 5th place finisher were separated by an average of 3.5 games (about 2.2%):

Note that no cases over this span even rise above the seven game “injustice line” of 5.75%, much less to the nightmare scenario of 7.5% that Stark invokes.  The standard deviation is about 1.5%, and that’s with the present imbalance of teams (note that the AL is pretty consistently higher than the NL, as should be expected)—after realignment, this plot should tighten even further.

Indeed, considering the typically small margins between contenders in baseball, on average, this “insane” sudden death series may end up being the fairest round of the playoffs.

Non-Sports Graph of the Day: National Debt v. Stock Market

I’m not really into finance, I’m not an economist, and I’m not trying to be Nate Silver, but I was messing around with some data and thought this was pretty interesting:

The blue line is based on the Wilshire 5000, which tracks the total market capitalization (share price times number of shares) of all publicly traded U.S.-based companies.  Data points for both measures are as of the close of the fiscal year.  The bright red dot is the projected national debt at the end of FY 2012, assuming no new budget deals are reached.

Hyperbole of the Day: Coach Ryan On Coach Belichick

And no, I don’t mean Rex:

“You can have Bill Parcells as a head coach and Vince Lombardi as a D-coordinator and Bill Walsh as the offensive coordinator and I think Belichick would beat them by two touchdowns if it came down to coaching,” Ryan said. “It’s going to come down to players and coaches and everything.”

From this ESPN article, which of course focuses on Rob Ryan’s opinion of Tom Brady.

Crazy hyperbole, though I’m not sure exactly what he means by “if it came down to coaching.”  Surely he doesn’t think that Belichick is better at all three skills: He is suggesting that Belichick has some super-quality that trumps mere offensive, defensive, and motivational strategies.

What strikes me as really funny, though, is the selection of Vince Lombardi as the “dream” defensive coordinator.  A much more natural choice would have been Buddy Ryan, but I guess Rob can’t very well go saying that Belichick would run laps around his own father.

10/9 NFL Sunday Live Blog

Alright, I made it. You know the drill, and if you don’t, details here.  Please leave comments and/or questions, etc.

1:40: Made it home just in time for the crazy ending of the Houston/Oakland game.  Interesting play within 2 minutes: Houston takes a sack, but is called for a personal foul/facemask.  Meanwhile, they go under the hood to check if Oakland had 12 men on the field, and they did.  By rule, the 12 men was declined, then the personal foul was accepted, with the end result being 1st and 25.  So the Oakland penalty is declined but still wipes out the sack?  Normally I pride myself on knowing all the obscure NFL rules, but this one was new to me.  Or maybe I missed something.

1:52: I got some questions this week about the purpose of the PUPTO metric, and how good it is as far as predicting future performance.  I’d say it’s more of a “story of the game(s)” stat than a “quality of the team” stat.  It does hold its own for predicting future outcomes, but there are a lot less crude methods in that area that are more effective (in general, turnovers should be handled more delicately).

1:55: Watching Jets and Patriots now, of course.

2:10: bottomofthe9th asks:

One other interesting question I was reminded of during that game–are timeouts over-used to avoid a delay of game penalty? Seems like they have to be, since 5 yards is almost inconsequential relative to your ability to run 3-4 extra plays late in the game. Of course it depends on what the probability is you’ll be coming back late in the game, but seems hard to believe it’s so low to justify burning a timeout just to avoid a 5-yard penalty.

I agree it would be interesting to quantify the actual value of a Time Out at various points in the game, but intuitively I’d guess that they’re not as valuable as you think.  They’re a bit like insurance, in that you’re super-glad that you had them when you need them, but I think the situations where a timeout makes much of a difference are more rare than you think.

For example, I’ve linked this before:

This table assumes you have the ball with 2 minutes left on the yardline indicated, and the four columns correspond to the number of timeouts you have.  Even on your own 10, the difference between 0 timeouts and 3 timeouts is less than 3%—and this is one of the more leveraged situations, you’d think (note: I can’t speak for the complete accuracy of the method FC used, but this is one of the few win % analyses out there I’ve seen that accounts for timeouts.  As I’ve noted before, ANFL Stats WPA Calculator does not include them).

2:18: So, from the earlier games, let’s see: Colts and Eagles lose again.  So maybe Peyton Manning is more valuable than a few wins, and maybe spending a lot of money on free agents isn’t a good way to get and NFL Championship.  I’m feeling like it’s about time for another one of my big “I Told You So” round-ups.

2:28: So here’s something I drew up on my iPad while I was without internet over the weekend.  It’s a generic visualization of a Punt/Go For It decision:

I have a longer post in the works that explains better and uses some actual data, but despite looking complicated, I think it’s actually a pretty simple way of analyzing these situations quickly.  In particular, it lets you adjust for relative team strength and/or type of offense without having to resort to complicated math (you can just “shock” the curves like you would in an econ class).

2:40: “Bills force late INT to finish off fading Eagles” is one of ESPN’s headlines for the Bills/Eagles game.  Not saying Vick didn’t screw the pooch in this one, but as I’ve been harping on the past couple of weeks, if there’s a time to risk throwing an interception, it’s when you’re down by 5 with under 2 minutes left.  If I were the coach and that drive ended with anything other than a touchdown or an interception, I’d be pissed.

2:46: I should make this a TMQ-like running item: “Interception of the Week,” celebrating the game-losing turnovers that happened at the most appropriate time to gamble.  It’s a bit like back when I played a lot of live poker: I used to record my “worst” river calls (where I called with some ridiculously weak hand and ended up being up against a monster), and then I’d brag about them to my friends.

2:51: Man, when did Wes Welker become New England’s “greatest asset”?  I remember when he was on the Dolphins, I thought he was underrated as a situational player, and I was unsurprised to see the Patriots pick him up.  Then his numbers went way up with Randy Moss, which I would have expected, and I kind of thought he got a bit overrated.  But now with Moss in the wind, he’s putting up even bigger numbers.  Crazy.

2:55: So my Quantum Randy Moss post—though the most popular non-Dennis Rodman post I’ve ever written—is one of my least brag-worthy in terms of results: Since I posted it (at the start of last season), Moss had his first 0 catch game, was dumped by two teams, was a non-factor on another, retired in a huff, and reportedly New England wouldn’t even take him back for less money.  I mean, I stand by my analysis, but what an unexpected disaster.

3:15: David Myers: I’ll look into that in a bit.  You could be right that I missed something, but it seemed to work out when I did it on paper.

3:20: So the “Reward” in that graph is the value of your drive times the odds of making the first down, and the “Risk” is the value of the opponent’s drive on the current LoS vs. where they would be expected to get the ball after a punt (times the chances of your failing to convert).  So you’re saying the green arrow on the left should extend to the opp’s drive value curve, but I’m not getting why.

Wouldn’t that be double-counting?

3:30: Nevermind, I get what you’re saying, misread your comment.  You’re saying you should also count denying the opponent a possession at all.  But outside of time-pressure scenarios, I don’t think that has any additional value (aside from what’s already covered in my proportions).

4:07: Argh, I’m getting bogged down in some database mechanics for an idea I was just having.  Note to self: don’t do massive original research projects during the live blog.

4:10: Myers expanded on his comment:

If you punt on play N, then the transition of scoring potential from play N to play N + 1 is from the green solid point to the red solid point, or A + C. The value of the _possession_ in turn has to be the additive inverse of that (plus whatever value is gained by the additional yardage made to get the first). Note this is logically equivalent to the argument about turnover value from The Hidden Game of Football (pp 102-103, 1988 edition). This valuation scheme is not original to me.

I’ll have to postpone looking into this until I have more time (love the academic citation btw).

4:52: Ugh, a little less than timely.  I was trying to find a more elegant way of doing this, but here’s a graph of the 2007 Patriots offense:

5:07: And here’s the comparison pic:

5:15: FWIW, the linear trendline equations for those two graphs are

y = .014x + 2.58

and

y=.036x + .49

respectively.

5:20: I just built those graphs from play-by-play data, which I started during the New England game (see, I was trying to reminisce about the crazy 2007 New England offense that you should never ever punt to).  Not only is that game over, but the night game is starting.  Sometimes I definitely overestimate my own speed.

5:23: Short break and I’ll be back with some crazy Aaron Rodgers stats.

5:40: Ok, quick side-product of what I was doing above: here’s a graph of expected points resulting from a 1st down on each yard line in the red zone:

6:02: Also, I don’t think the variations in that graph are all noise.  First, the sample is pretty huge (n=15,088),  and it’s consistent with other research I’ve done about the bizarre things that happen with a “compressed field.”  Here are some of the features that I can see and the theoretical justifications:

  1. There’s a decline right before the 10 yard line, with the 10 yard line itself being a pretty serious local minimum.  I think this happens because of the shortened field and the increasing difficulty of getting a first down without getting a touchdown (e.g., from the 11 yard line, you can only get a first down inside the 1, but from the 13 yard line you have 3 yards to work with).  This is relevant b/c the odds of a touchdown on any given play from the 10, 11, 12 aren’t that different.
  2. There’s a flattening that occurs between the 20 and the 15: I think this is where you first experience “compressed field” issues (less room for receivers to run).  But then around the 15, I think the effect is “complete” (at least for a while), and the natural advantage of being closer takes over again.
  3. There’s a “statistically significant” outlier on the 3 yard line, where 1st and goal on the 3 is actually less valuable than 1st and goal on the 4.  I’m fairly certain that this at least in part due to configuration issues (as you have limited offensive options on the 3), though I think it may also be caused by poor play selection.  Specifically, teams call a much higher percentage of running plays from the 3 than from the 4, while defenses are pretty much always stacked against the run.
  4. The slope at the 10 going down to the 8 is somewhat greater than in other areas of the graph where the expectation is increasing linearly (incidentally, as I mentioned 2 weeks ago, this is one of the things that makes EPA and WPA models difficult: you have some pretty dramatic shifts over a small number of yards, and you can’t really model it with a continuous equation).  This effect I also think might have something to do with play selection, or even 2nd-order play selection: that is, teams pass a fair amount, which is good, running is also fairly effective (b/c defenses are more focused on pass), and successful runs often leave them at a yardline (like the 4+) where they are still willing to pass.

Really, it may seem crazy, but I’ve looked into most of these effects and have found support for them.

6:36: Ok, as I’ve noted before, Rodgers’ consistently low interception % is pretty unusual, though of course his sample size is tiny:

Now let’s compare to the rest of the league (starting at least 8 games):

Obviously he is way on the left side of this blob, and his “slope” (if you can call it that with only 3 points so far) is much higher.

6:40: Let’s compare to Peyton Manning:

Rodgers’ Int% with a 40% win rate is almost half that of Peyton Manning’s (and, it goes without saying, Manning is a pretty consistent QB).

6:45: And, of course, what Rodgers analysis could be complete without comparison to Brett Favre:

6:52: I should note, of course, that I have no problem with Favre or Manning’s numbers here.  I cite Rodger’s consistency not b/c I think it’s necessarily better, but just b/c it’s interesting.  I would expect a QB to have a higher Int% when playing for a losing team, whether he is consistent or not.  Generally, I think a relatively high “shot group” on this graph, with a relatively low slope, can be a good thing: It may simply reflect that the QB is taking necessary risks when required to (though, clearly, isolating the causes and effects is incredibly difficult).

7:00: I see Tiger Woods bounced back with three 68’s in a row in the Frys.com tournament.  He finished tied for 30th.  In what is basically a “Quest for the Card” tournament.  In a field that contained 9 of the world’s top 100 players.

Comeback?

7:15: Atlanta is such a sneaky franchise. They seem to be competitive every couple of years, putting together good-to-great regular seasons, but haven’t won more than one playoff game since 1998.  I think you can win with great passing and great running, great defense and great running, but you can’t win with great running alone.  Their performance, to me, seems like a classic run good/run bad situation, where they probably haven’t changed all that much year to year, but being a little better than average keeps them occasionally in contention (while still being at a disadvantage against the actually better teams that they have to face in the playoffs).

7:42: Rodgers has a sick Adjusted Net Yards Per Attempt (generally considered the best non–play-by-play single QB metric) this season, leading the league with 9.7 going into this weekend.

So, out of curiosity, I was kind of curious just how much better ANY/A is than the pariah of QB stats: the NFL Passer Rating.  So here are a couple of simple scatter-plots, ANY/A first:

And here’s PER:

ANY/A obv does better, though maybe not as much as I would have guessed.

7:47: Of course, both stats are subject to causation/entanglement issues, ANY/A possibly even moreso (as it includes sacks and weights interceptions more heavily).

7:54: That style of touchdown where a receiver has one defender, breaks for the sideline, then turns, leaps and stretches out for the touchdown, is always hailed as a great play, despite being completely textbook and despite being executed pretty much exactly the same way by every receiver in the NFL—normally differing only by whether they are close enough and have a good enough angle to get inside the pylon.

7:58: Man, I’m excited for Detroit/Chicago tomorrow.  Can’t remember the last time I thought that.

8:14: Ok, I can’t help but return to this David Myers point from earlier:

If you punt on play N, then the transition of scoring potential from play N to play N + 1 is from the green solid point to the red solid point, or A + C. The value of the _possession_ in turn has to be the additive inverse of that (plus whatever value is gained by the additional yardage made to get the first).

I don’t think the possession has value in addition to its scoring potential, or at least not as much as you’re suggesting.  This method you’re describing counts the value of not giving the opponent the ball in addition to the value of keeping the ball for yourself.  But I really think you shouldn’t do that, since you haven’t decreased the expected possessions for the game of your opponent—or, at least, you certainly haven’t decreased it by 1.  They are still going to get the ball when your possession is over.  By holding the ball now, you make it slightly more likely that the last drive of the game will be yours (depending on how much time is left, etc), but you’re still going to be trading possessions 1 for 1.

For an analogy, think of rebounding in basketball: Occasionally I’ve heard casual fans suggest that offensive rebounds must be more important than defensive rebounds because you not only get a possession but you take one away from your opponent.  But this is strictly false: A rebound is worth one possession regardless (note, of course, offensive rebounds probably are more valuable than defensive rebounds, but only because you are less likely to get them).  What you gain by getting an offensive rebound is exactly your expectation for your new possession, b/c the other team is still going to get the ball back when it’s over.  I can’t see any distinction between this and converting a 4th down.

8:24: Also, it’s true that, depending on where you are on the field, your opponent may be expected to get the ball back in a worse position.  But this effect should be included in whatever you use for value on the Y-axis.  At least, a perfect metric for the Y-axis would include it (though I think a proxy like expected points is good enough for most approximations, which is what that graphing method is all about).

8:29: Wow, can’t wait for that Packers/Chargers game.

8:32: Game, set, match.  Respect to Aaron Rodgers for breaking a Kurt Warner record (PER over first 1500 attempts).  Was there anything more incredible in the history of football than the 1999 Rams?

Punts are Turnovers Too (Introducing PUPTO!)

[For ease of reference—with apologies to those of you who sat through or otherwise already read my NFL Live Blog from this Sunday—I’m once again splitting a few of the topics I covered out into individual posts. I’ve made mostly made only cosmetic adjustments (additional comments are in brackets or at the end), so apologies if these posts aren’t quite as clean or detailed as a regular article. For flavor and context, I still recommend reading the whole thing.]

[I removed the “From the Live Blog” tag from the title of this post, because 1) I added a bit more explanation in my Addendum below, 2) The original discussion was at the very end of my very long live-blog post and a lot of people prob didn’t get to it anyway, and 3) I just think it’s an important issue and I don’t want to scare people away.]

With all the turnovers in [the Jets and Ravens] game, there’s about a 100% chance that commentators later will talk about the importance of “turnover differential.”  People always rattle off a bunch of stats about how the team that wins the “turnover battle” almost always wins the game (like, duh), with the intention of reminding everyone how terrible it is to take the kinds of risks that lead to turnovers.

But this causation goes both ways: Turnovers can obviously cause teams to lose, but teams losing also cause turnovers.  When you’re behind, you have to take risks to have any chance of winning. Citing the “turnover battle” stats without context is about as ridiculous as [the also way-overused] “Team X is 43-1 when having a 100 yard rusher.”

What goes unmentioned in all of this is “punt differential.” But punts also involve turning the ball over, and guess what? This stat is ALSO highly predictive of game outcomes, but without as much causation baggage: When teams are behind, they are actually forced to punt less.  Despite the completely routine nature of punts vs. the “extreme” nature of turnovers, “punt differential” holds its own with “turnover differential” in a logistic regression to Win % (n=5308):

If you run this as a linear regression to point differential, it gets even closer (I should also note, if you do your regression to “outside” games, punt differential is actually more predictive, because it is much more reliable).

A fun metric that I love (and believe to be very useful) is “punts plus turnovers,” or PUPTO [Make it big, people!]:

A pretty interesting thing to note in this chart is the difference between the correlation to win % of interception differential vs. fumble differential.  From a pure “Turnovers=Bad” perspective, this should be counter-intuitive: After all, many interceptions take place down-field, while fumbles typically happen at the line of scrimmage (also, I haven’t checked, but I feel like a disproportionate number of fumbles are returned for touchdowns).  My suspicion is that this difference is at least partly [on reflection, probably mostly] explained by what I described earlier: When teams are losing, they have to take a lot of risks that lead to more interceptions, [i.e., passing a lot] but they don’t take a lot of risks [or at least as many] that lead to more fumbles.

Addendum:

To make this a bit more clear (I hope), the point is that the difference in fumbles lost should be a pretty “pure” metric for representing the consequences of turnovers.  This is because they happen much more randomly than interceptions, which (both rationally and empirically) increase in frequency significantly when a team is already behind.  So imagine this effect didn’t exist, and interceptions were distributed more like fumbles: we would expect the “INT Diff” bar in the chart above to drop closer to where the “Fum Diff” bar is, and consequently the “TO Diff” bar would drop as well.  The “PUPTO” bar—though obviously dropping a little itself—would comparatively tower over the rest.  So I don’t just love PUPTO for the way it sounds: I think it’s actually a powerful metric.

Not to mention, if I somehow had the power to instantly mainstream it, it might dampen a little bit of the stigma against “going for it” on 4th down: one of the things sports commentators and talking heads constantly seem to forget is that punts are bad too.

From the Live Blog: Drive Outcomes From Deep in Your Territory

[For ease of reference—with apologies to those of you who sat through or otherwise already read my NFL Live Blog from this Sunday—I’m once again splitting a few of the topics I covered out into individual posts. I’ve made mostly made only cosmetic adjustments (additional comments are in brackets or at the end), so apologies if these posts aren’t quite as clean or detailed as a regular article. For flavor and context, I still recommend reading the whole thing.]

[See also my Addendum below.]

Random stat from my PBP database:  For home teams, 19% of drives starting with a kickoff end in a touchdown, for away teams, just under 17%.  But on the first drive of a game, home teams score TD’s on 22%, away teams just 16%.

Any time I start wading through PBP stuff, I get easily distracted.  There’s something new and fascinating around every corner! [E.g.], here’s what should be considered a pretty basic graph, but it has some interesting subtleties to it:

One of the most interesting parts is what’s going on in the first 20 yards:

So what’s interesting about this? Well, that aside from safeties, these particular results are very linear.  I think many people would expect that being backed into your endzone makes executing your offense a lot harder — but aside from the occasional safety, the outcomes are really no worse than what you would expect from just being more yards back (turnovers aren’t shown b/c of data mashing issues, but there’s not a massive jump for them either).

Of course, another important factor [is the effect on punting]:

And, the corresponding graph limited to your own 20:

So the take-homes from the above graphs are that the situation gets significantly better/worse within the 5 yard line, accelerating as you approach the goal line.  [Though the effect may not be as apparently strong as some probably thought,] this is why kicking field goals from the 1 is terrible even in situations where it has some tactical benefit.  Obv this is nothing new to anyone even slightly informed about “expected value” in football (it’s basically the prototypical example), but to break it down clearly: If you don’t score on your 4th down play, trapping your opponent in that spot is valuable 4 ways:

  1. Natural field position advantage vs. giving your opponent the ball on the 20 after a made field goal.
  2. Significantly increased chance of a safety.
  3. Increased chance of good field position b/c of short opponent punts.
  4. Your subsequent field position also starts to hit the increasing part of your Touchdown/Expected Points curve (i.e., it has value in addition to the generic value of better expected field position).

Though it should be noted that the last 3 effects are much stronger on the 1 than on the 5.

Matt notes:

I was just able to use the drive expectancy chart to check on a Chris Collinsworth comment, love all the graphs and tools. BTW the comment was about the value of getting the ball on the 2-3 vs the half yard line, if I read the graph right the odds of a safety double at the 1 yard line vs the three yard line. Still only 6% but a big enough difference to care.

Yes, there’s a significant difference between the two, and it gets more and more dramatic the closer you get to the plane: there’s a pretty significant difference from being at the 1 and being at the 1/2, etc.  It’s also true on the other side of the field: all kinds of wacky things happen as you approach the Endzone, and they’re not all intuitive.

In fact, one of the big difficulties with building a [Win Percentage Added] model is accounting for these kinds of situations empirically, because 1) they behave abnormally, and 2) they’re either rare (e.g., being right at your own end zone), or extremely specific (e.g., some of the things that happen around the 11-12 yard line in the Red Zone), and thus have some of the smallest sample sizes for observation.

Addendum:

David Myers (of Code and Football) also comments:

Why ask? I think the result is important, and I was curious how reliable the data set was. 9 years is a lot of data [note: it’s actually 10 years].

A further explanation would be this: I’m curious why the expected points curves of, say, Keith Goldner and Bill Connelly and Romer/Burke are different. I’ve speculated on the difference here. Your plot suggests that different drive scoring has to be at the root of those differences, as safeties alone can’t account for the first and 10 expected points curves I’ve seen.

Yes, this is what I was getting at in that last paragraph.  It’s a bit like physics: it’s easy to build models that explain all the common and relatively simple situations. But it gets much more difficult in the extremes, which can be more complicated, often have less data to analyze, and what data is available is often less reliable.

From the Live Blog: Baseball Haterade (With NFL Regression Tangent)

[For ease of reference—with apologies to those of you who sat through or otherwise already read my NFL Live Blog from this Sunday—I’m once again splitting a few of the topics I covered out into individual posts. I’ve made mostly made only cosmetic adjustments (additional comments are in brackets or at the end), so apologies if these posts aren’t quite as clean or detailed as a regular article. For flavor and context, I still recommend reading the whole thing.]

In support of last night’s screed [Why Baseball and I are, Like, Unmixy Things], especially the claim that “[MLB] games are either not important enough to be interesting (98% of the regular season), or too important to be meaningful (100% of the playoffs),” here’s a graph I made to illustrate just how silly the MLB Playoffs are:

Not counting home-field advantage (which is weakest in baseball anyway), this represents the approximate binomial probability [thank you, again, binom.dist() function] of the team with the best record in the league [technically, a team that has an actual expectation against an average opponent equal to best record] winning a series of length X against the playoff team with the worst record [again, technically, a team that has an actual expectation equal to worst record] going in.  The chances of winning each game are approximated by taking .5 + better win percentage – worse win percentage (note, of course, the NFL curve is exaggerated b/c of regression to the mean: a team that goes 14-2 doesn’t won’t actually win 88% of their games against an average opponent. But they won’t regress nearly enough for their expectation to drop anywhere near MLB levels).  The brighter and bigger data points represent the actual first round series lengths in each sport.

By this approximation, the best team against the worst team in a 1st round series (using the latest season’s standings as the benchmark) in MLB would win about 64% of the time, while in the NBA they would win ~95% of the time.  To win 2/3 of the time, MLB would need to switch to a 9 game series instead of 5; and to have the best team win 75% of the time, they would need to shift to 21 (for the record, in order to match the NBA’s 95% mark, they would have to move to a 123 game series.  I know, this isn’t perfectly calculated, but it’s ballpark accurate).  Personally, I like the fact that the NBA and NFL postseasons generally feature the best teams winning.

Moreover, it also makes upsets more meaningful: since the math is against “true” upsets happening often, an apparent upset can be significant: it often indicates—Bayes-wise (ok, if that’s not a word, it should be)—that the upsetting team was actually better.  In baseball, an upset pretty much just means that the coin came up tails.

Adam asks:

In the MLB vs. NFL vs. NBA Playoffs graph, the chances of best beating worst in first round for NFL for a 1 game series is almost 95%.

Looking at the odds to this week’s NFL games, the biggest favorite was GB verses Denver and they were only an 88% chance of winning by the money line (-700). Denver is almost certainly not a playoff team, so it’s tough to imagine an even more lopsided playoff matchup that could get to 95%. What am I missing?

I sort of addressed this in my longer explanation, but he’s not missing anything: the football effect is exaggerated. First off, to your specific concern, this early in the season there is even more uncertainty than in the playoffs.  But second, and more importantly, this method for approximating a win percentage is less accurate in the extremes, especially when factoring in regression to the mean (which is a huge factor given the NFL’s very small sample sizes).

In fact, the regression to the mean effect in the NFL is SO strong, that I think it helps explain why so many Bye-teams lose against the Wild Card game winners (without having to resort to “momentum” or psychological factors for our explanation).  By virtue of having the best records in the league, they are the most likely teams to have significant regression effects.  That is, their true strength is likely to be lower than what their records indicate.  Conversely, the teams that win in the bye week (against other playoff-level competition), are, from a Bayesian perspective, more likely to be better than their records indicated.  Think of it like this: there’s a range of possible true strength for each playoff team: when you match two of those teams against each other (in the WC round), the one who wins might have just gotten lucky, but that particular result is more likely to occur when the winning team’s actual strength was closer to the top of their range and/or their opponent’s was closer to their bottom.

I’ve looked at this before, and it’s very easy to construct scenarios where WC teams with worse records have a higher projected strength than Bye team opponents with better records.  Factor in the fact that home field advantage actually decreases in the playoffs (it’s a common misconception that HFA is more important in the post-season: adjusting for team quality, it’s actually significantly reduced—which probably has something to do with the post-season ref shuffle: see section on ref bias in this post), and you have a recipe for frequent upsets.

In retrospect, I probably should have just left the NFL out of that graph.  Basketball makes for a much better comparison [both aesthetically and analytically]:

From the Live Blog: More on Cam Newton

[For ease of reference—with apologies to those of you who sat through or otherwise already read my NFL Live Blog from this Sunday—I’m once again splitting a few of the topics I covered out into individual posts. I’ve made mostly made only cosmetic adjustments (additional comments are in brackets or at the end), so apologies if these posts aren’t quite as clean or detailed as a regular article. For flavor and context, I still recommend reading the whole thing.]

[This is sort of following up on last week’s live blog, where I discussed Cam Newton’s hot start a little, so I’ll include that snip first.]

Last Week, On Cam Newton:

Watching pre-game.  Strahan is taking “overreaction” to a new level, not only declaring that maybe the NFL isn’t even ready for Cam Newton, but that this has taught him to stop being critical of rookie QB’s in the future.

But should I be more or less excited about Cam Newton after his win today?  He had a much more “rookie-like” box of 18/34 for 158.  Here’s how to break that down for rookies: Low yards = bad. High attempts = good.  Completion percentage = completely irrelevant. Win = Highly predictive of length of career, not particularly predictive of quality (likely b/c a winning rookie season gets you a lot of mileage whether you’re actually good or not). Oh, and he’s still tall:  Height is also a significant indicator (all else being equal).

This week:

Google search that just led to the blog: “should I start Michael Vick over Cam Newton today.”  Welcome, fantasy footballer!  And sorry, I have no idea.  I don’t play fantasy football anymore: it’s pleasantly time consuming and has near-infinite depths for analysis, but the overlap with analysis of things that matter is way too small. [This was a bit harshly put, but I mean something serious: I’m increasingly convinced that NFL box score accomplishments have little relation to actual player values].

Here’s rookie QB’s YPG over their first 3 starts [actually, it’s games played, not started—my bad] vs. their YPG for the rest of the season (min 8 starts total):

And here’s the table of rookies through Dan Marino (who I thought would have been higher):

Cam Newton, of course, has 1012 through his first 3.  And in game 4 he has already passed Vinny Testaverde’s production for the rest of his rookie season.

[At the conclusion of the game] Newton now has 1386 yards, which is the record for a rookie through his first four games (previously held by Marc Bulger with 1149).  The record through five is 1496, so he’s likely to break that.  Through six is 1815, so that’s not a sure thing, but through seven is also 1815 (Bulger only played 6 games, and the next highest total through seven is 1699).  But there’s still a lot of variance to be navigated between now and [Peyton] Manning’s full-season record of 3739.