As promised, I’ll be live-blogging all day. Details here.
I’ll finally be getting NFL Sunday Ticket later this week (DirecTV is cheaper than cable, who knew?), but for now I’m stuck with what the networks give me. As of last night, I thought the early game was going to be New England against Buffalo, but now my channel guide is saying Philadelphia/Giants. I’ll find out in a few minutes.
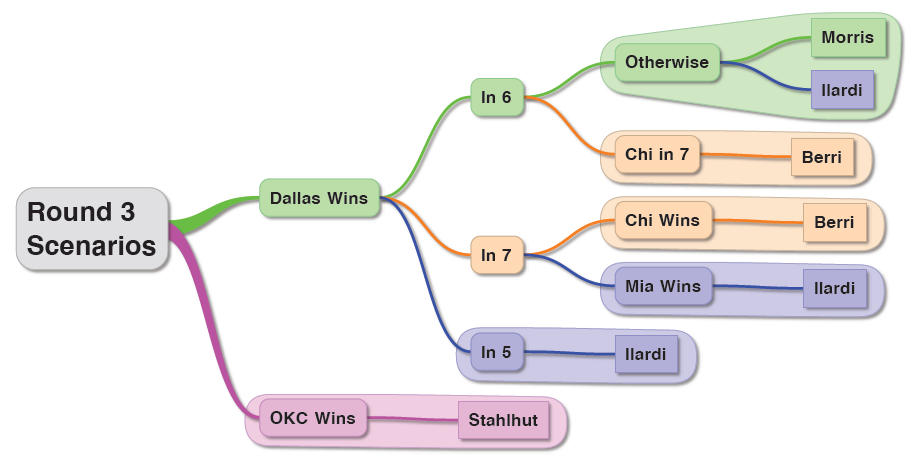
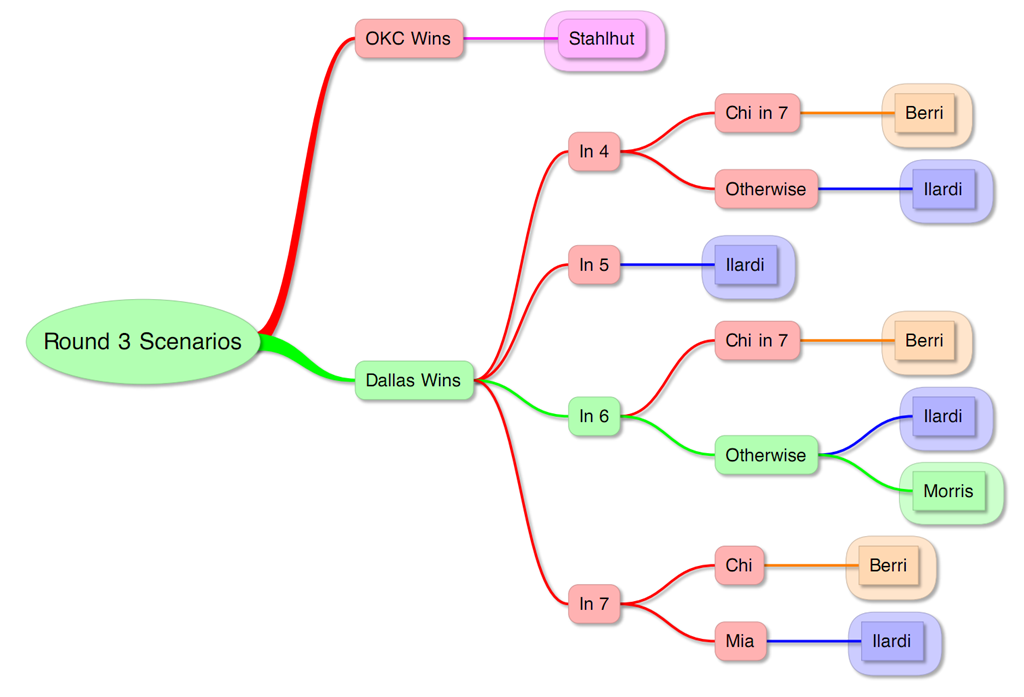
This may not be the most controversial statement, but I think the two most powerful forces in the NFL over the last decade have been Peyton Manning and Bill Belichick (check out the 2nd tab as well):
I’m sure I’ll have more to say about the Great Hoodied One over the course of the day, so, for now, on with the show:
9:55 am: Watching pre-game. Strahan is taking “overreaction” to a new level, not only declaring that maybe the NFL isn’t even ready for Cam Newton, but that this has taught him to stop being critical of rookie QB’s in the future.
10:00 am: CBS pregame show over and now it’s a paid advertisement for the Genie Bra (I’m so tempted). And, yep, Fox has the Philly game.
10:10: In case you haven’t seen it, the old “Graph of the Day” that I tweaked for the above is here.
10:15: Nothing wrong with that interception by Vick. Ugh, commercials. I hate Live TV, especially when there’s only one thing on.
10:20: Belichick, of course, is known for winning Super Bowls, going for it on 4th down, and:
Good thing he doesn’t have to worry about potential employers Googling him.
10:24: Manning gets first blood in this battle of “#1 draft picks who everyone was ready to give up on but then performed miracles.”
10:30: True story: Yesterday, my wife needed a T-shirt, and ended up borrowing my souvenir shirt from SSAC (MIT/Sloan Sports Analytics Conference). She was still wearing it when we went to see Moneyball last night, and, sure enough, she ended up liking it (nerd!) and I thought it was pretty dull.
10:35: David: Wins in season n against wins in season n+1. Sorry, maybe should have explained that.
10:39: Aaron Schatz tweeted:
Bills go for it on fourth-and-14 from NE 35… and Fitzpatrick throws his second pick (first that is his fault)
4th and 14 is a situation where I think more quarterbacks throw too few interceptions than throw too many.
10:48: Tom Coughlin thinks LeSean McCoy is the fastest running back in the NFL? Which would make him faster than Chris Johnson? Who thinks he’s faster than Usain Bolt? What is he, a neutrino?
11:00: O.K., per Matt’s request, I’ve added a “latest updates” section to the top. Let me know if you like this better.
11:05: And sorry about the neutrino joke. Incidentally, it probably goes without saying, but CJ is not as fast as Bolt in the 40. Bolt is the fastest man on earth at any distance from 50 meters to 300. I’ll post graphs in a bit.
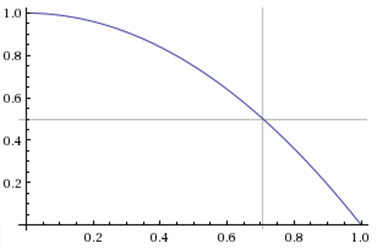
11:17: Man, I am having all kinds of browser problems. May have to switch computers. Anyway, here’s a Bolt graph:
Since we know his split time (minus reaction) over 32.8 yards was 3.64 seconds, using the curve above we can nail down his time at 40 yards pretty accurately: it’s around 4.19 to 4.21. (Note, the first 50 Meters of Bolt’s 100M world record were faster than the record for 50 meters indoors.)
11:25: Incidentally, Chris Johnson’s 40 time of 4.25 is bogus. I won’t go into all the details, but I’ve calculated his likely 40 time (for purposes of comparison with Bolt), and it’s more like 4.5. Of course, that’s a bit of “apples to oranges” while combine times vs. each other are “apples to apples,” but the point is that Bolt’s advantage over CJ is much bigger than .05.
11:28: Ok, halftime. Unremarkable game so far, though Eli got a good stat boost from a couple of nice catch-and-runs. I would love to see how Vick performs under pressure, so I’m glad they’ve gotten close again. Going to grab a snack.
11:44: Matt: I’ve seen a few things, but I don’t have the links in front of me. Prior to Berlin, Usain was definitely known as a slow starter with a crazy top speed that made up for it, but in his 9.58 WR run he was pretty much textbook and led wire to wire, posting the fastest splits ever at every point.
11:58: Lol, everyone loves when linemen advance the ball. Until they fumble. Then they’re pariahs.
12:07: I haven’t really used Advanced NFL Stats WPA Calculator much, as I’ve been (very slowly) trying to build my own model. But I just noticed it doesn’t take time outs into account. I’m curious whether that’s the same for his internal model or if that’s just the calculator. Obv timeouts make a huge difference in endgame or even end-half scenarios (and accounting for them properly is one of the toughest things to figure out).
12:11: Man, I was just thinking how old I must be that I remember the Simpson’s origins on the Tracy Ullman show, but the Fox promo department made me feel all better by viscerally reminding me that they’re still on.
12:14: Google Search Leading to My Blog of the Day: “what sport does dennis rodman play”
12:22: So Both Donovan McNabb and Michael Vick have been considerably better QB’s in Philadelphia than elsewhere. At some point, does Andy Reid get some credit? Without a Super Bowl ring, he’s generally respected but not revered in the mainstream, and he’s such a poor tactician that he’s dismissed by most analytics types. But he may be one of the best offensive schemers in the modern era.
12:34: Moneyball nit-picking: The Athletics won their last game of the season in 2004, 2005, 2007, and 2010. (It’s not that hard when you don’t make the playoffs).
12:40: I kind of feel the same way about Vick that I felt about Stephen Strasbourg after he hurt his arm last year: their physical skills are so unprecedented that, unfortunately, Bayesian inference suggests that their injury-proneness isn’t a coincidence.
12:45: David: I just mean that he has notoriously bad time management skills, makes ridiculous 4th down decisions, and generally seems clueless about win maximization, esp. in end-game scenarios.
12:48: So if the Eagles go on to lose, does this make Vick 1-0 with 2 “no decisions” for the year?
12:54: Wow, Tom Brady has as many. . . Crap, Aaron Schatz beat me to it:
Tom Brady has as many INT in this game as he had all last year. Egads.
12:57: Dangit, exciting New England end-game and I’m stuck watching the Giants beat Vick’s backup. Argh!
1:03: Really Moneyball is all about money, not statistics. Belichick would be such a better subject for a sports-analytics movie than Billy Beane. It’s dramatic how Belichick has been willing to do whatever it takes to win—whether it be breaking the rules or breaking with convention—plus, you know, with more success.
1:06: “Bonus Coverage” on Fox is Detroit v. Minnesota. CBS just started KC/San Diego.
1:14: Top-notch analysis from Arturo:
Holy effin Christ. Bills/Pats4 minutes ago
1:19: Nate: Are you referring the the uber-exciting Pats/Bills game that I can’t watch? I’ll check the p-b-p.
1:27: Congrats Nate and Lions fans everywhere!
1:30: Ok, I’m going to take a short lunch break, I’ll be back @ 2ish PST.
2:05: Nate asks:
Any thoughts on the Lions kicking a 32-yard FG in overtime from the left hash on first down?
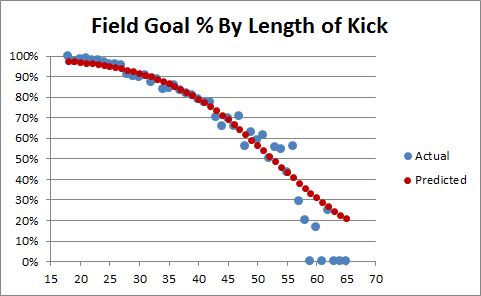
I’ve thought about this situation a bit, and I don’t hate it. Let me pull up this old graph:
So a kneel in the center is maybe slightly better: generically, they lose a percentage or two, but I’m pretty sure that even from that distance you lose a percentage or two for being on the hash. Kickers are good enough at that length that going for extra yards or a TD isn’t really worth it, plus you’re not DOA even if you miss (while you might be if you turn the ball over).
2:08: Btw, I’ve got Green Bay/Chicago of Fox to go with aforementioned KC/SD on CBS.
2:12: Also from that post where the graph came from, the “OT Choke Factor” for kicks of that length is negligible.
2:35: So this Neutrino [measured as faster-than-light, in case you’ve been living under a rock or aren’t a total dork] situation is pretty fascinating to me. What’s amazing is that, even days later, no one has been able to posit a good theory for either the result-as-good OR where the error might be coming from.
Note this wasn’t like some random crackpot scientist, this was a massive team at CERN, which is like the Supreme Court of the particle physics world.
It’s a bit like if you brought the world’s best mathematicians and computer scientists together to design a simple and effective way to calculate Pi, only to have it spit out 3.15. It just can’t possibly be, yet no one has a good explanation for how they screwed up.
To complicate things further, you have previous, “statistically insignificant” results at MINOS that also clocked neutrinos as FTL. Indepedently, this should be irrelevant, but as a Bayesian matter, a prior consistent result — even an “insignificant” one — can exponentially increase the likelihood of the latter being valid. If it had been any other discovery, this would be iron-clad evidence, and it would probably be scientific “consensus” by now.
So, as a second-order observation, assuming they eventually do find whatever the error may be in this case, doesn’t it suggest that there may be other “consensus” issues with similarly difficult-to-find errors underlying them that were simply never challenged b/c they weren’t claiming that 2+2=5?
2:36: Ok, I think I’m required by Nerd Law to post the XKCD comic on the topic:
2:41: Added links.
2:43: Argh. NFL Live Blog, I know. Sorry.
2:52: News says that a 3.3 earthquake “hit” Los Angeles today. Um, 3.3. I’m pretty sure that’s also known as “not an earthquake.”
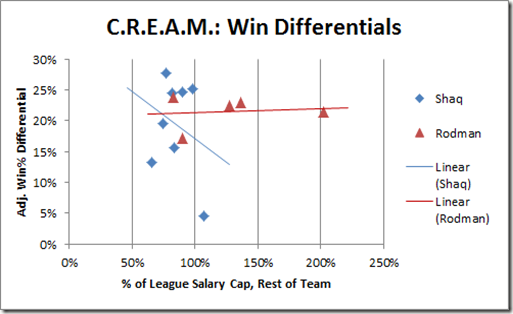
3:05: OK, this has little to do with the game I’m “watching” (something about the non-Detroit NFC central bores me now with Favre gone and Lovie/Martz coaching in Chicago), but here’s a brand new (10 minutes old) bar chart from my salary study:
Obv this stuff becomes more meaningful in a regression context, but it’s interesting even at this level. A little interpretation to follow.
3:20: “Overspending” is the total amount spent above the sum of cap values for all your active players, like “loading up” on one year by paying a lot of pro-rated signing bonuses. For position players, their cap value is the best (salary-based) predictor of their value, so, unsurprisingly, teams with high immediate cap values tend to have the better teams (while total money spent also correlates positively, it’s entirely because it also correlates with total cap value).
What’s interesting about running backs is that RB cap value correlates positively, but signing bonus correlates negatively. My unconsidered interpretation is that RB’s are valuable enough to spend money on when they’re actually good, but they’re too hard to evaluate to try to buy yourself one.
3:36: Matt Glassman asks:
Question re: field goals — What percentage are you looking for your kicker to have at the longest range you are willing to regularly (i.e. throughout the game) use him?
I’ll use a static example: if your kicker was a known 50% from 52 yards, would you regularly take that over a punt? What about 40%, etc. Then make it dynamic, where the kicker has some shrinking probability as he moves back, and the coach has a decision about whether to kick/punt from a given distance. At what maximum distance/percentage do you regularly kick, rather than regularly punt.
This is a good question and topic, but it’s extremely hard to generalize. It depends on your game situation and what your alternatives are. Long kicks, for example, are generally bad—even with a relatively good long-range kicker. But in late-game or late-half scenarios, clearly being able to take long kicks can be very valuable.
It is demonstrable, however, that NFL kickers have gotten incredibly good compared to past kickers. Aside from end-game scenarios, kicking FG’s used to be almost universally dominated by going for it (or sometimes punting). But since kickers have become so accurate, the balance has gotten more delicate.
Also [sort of contra Brian Burke, I’m thinking of a link but can’t find it], I think individual team considerations are a much bigger factor in these decisions than just raw WPA. It depends a lot on how good your offense is, how good it is at converting particular distances, how good your defense is, etc. While the percentage differences may be fairly small for the instant decision, they pile up on each other in these types of multi-pronged calculations.
3:50: I have to admit, Aaron Rodgers is a great QB who seems to defy my “Show me a QB who doesn’t throw interceptions, and I’ll show you a sucky quarterback” rule of thumb. And it’s not like Tom Brady, who throws INT’s when his team is struggling and doesn’t throw them when his team is awesome (which, ofc, I have NO problem with): Rodgers has a crazy-low INT rate on a team that has been mediocre (2008), good-but-not-great (2009), or all over the place (2010) during his 3 years as a starter.
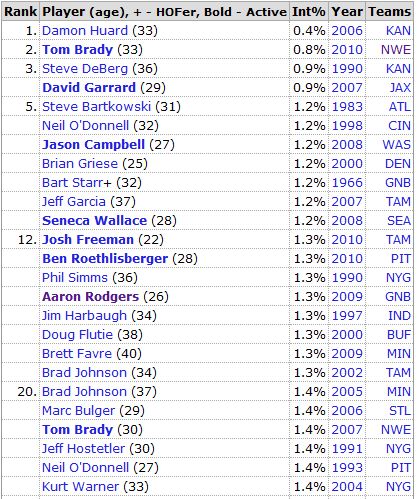
4:05: Ok, purely for fun, let’s compare the all-time single-season leaders in (low) Int% (from Pro Football Reference):
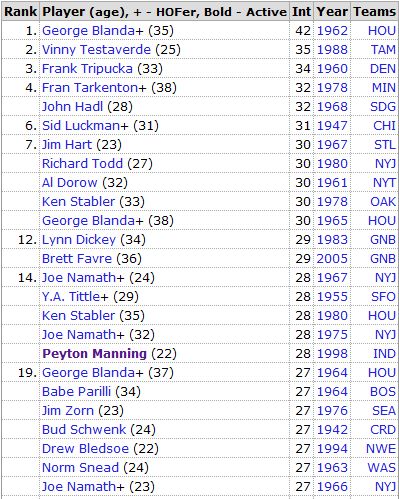
With the all-time leaders for most INT thrown (also from Pro Football Reference):
Not drawing any conclusions or doing any scientific comparisons, but both lists seem to have plenty of studs as well as plenty of duds. (Actually, when I first made this comparison a couple of years ago, the “Most” list had a much better resume than the “Least” list. But since then, the ‘good’ list has added several quality new members.)
4:11: O.K., I think I’m switching to Football Night in America. Peter King! He was the first sports columnist I ever read regularly (though eventually I stopped). I mean, he talks and writes completely out of his ass, but there’s a kind of refreshing sincerity about him.
4:24: So should I be more or less excited about Cam Newton after his win today? He had a much more “rookie-like” box of 18/34 for 158. Here’s how to break that down for rookies: Low yards = bad. High attempts = good. Completion percentage = completely irrelevant. Win = Highly predictive of length of career, not particularly predictive of quality (likely b/c a winning rookie season gets you a lot of mileage whether you’re actually good or not). Oh, and he’s still tall: Height is also a significant indicator (all else being equal).
Short break, back in a few.
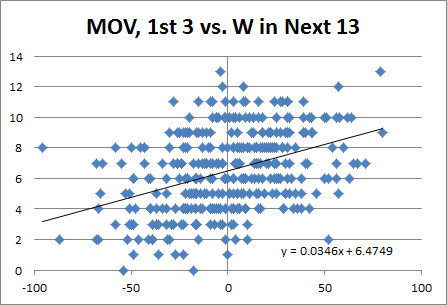
4:43: Detroit is currently 3-0 and leading the league in Point Differential at +55, and unlikely to be passed by anyone any time soon [by which I mean, this weekend].
4:58: That +55 would be the 16th best since 2000. Combined with their 3-0 record, they project to win ~11 games, though with lots of variance:
Yes, this can be calculated more precisely, but it will be around 11 games regardless.
5:12: The teams who led in MOV after 3 weeks since 2000 were:
- 2010: Pittsburgh, +39, Lost Super Bowl
- 2009: New Orleans, +64, Won Super Bowl
- 2008: Tennessee, +43, Lost Divisional
- 2007: New England, +79, Lost Super Bowl
- 2006: San Diego, +57, Lost Divisional
- 2005: Cincinatti, +60, Lost Wild Card
- 2004: Seattle, +52, Lost Wild Card
- 2003: Denver, +65, Lost Wild Card
- 2002: Miami, +63, Missed Playoffs
- 2001: Green Bay, +80, Lost Divisional
- 2000: Tampa Bay, +67, Lost Wild Card
Not bad. Only Miami missed the playoffs, and they were in a 3 way tie atop AFC East at 9-7.
5:23: I hate to keep going back to Schatz, but he posts so much and so fast that he’s dominating my Twitter feed. Anyway, the latest:
Weird week for FO Premium picks. 8-6 vs. spread (4-0 Green/Yellow) but 5-9 straight up.
In 2002, I picked better against the spread than straight up over the entire season (picking every game).
5:34: Shout-out to Matt Glassman for plugging my live blog on his:
One look at his blog will convince you that he’s not only a killer sports statistician, but he’s also an engaging and humorous writer.
Though, at best, this generous praise is a game of “Two Truths and a Lie.” [I’m not even remotely a statistician.]
5:39: If I were more clever, I’d think of some riff off the Jay-Z’s 99 problems line:
Nah, I ain’t pass the bar but i know a little bit
Enough that you won’t illegally search my shit
Incidentally, love the Rap Genius annotation for that lyric (also apt to my situation):
If you represent yourself (pro se), Bar admission is not required, actually
5:55: Since I’m obv watching the Indy game, a few things Peyton Manning coming up. First, a quick over/under: .5, for number of Super Bowls won by Peyton Manning as a coach?
I mean, I’d take the under obv just b/c of the sheer difficulty of winning Super Bowls, but I’d be curious about the moneyline.
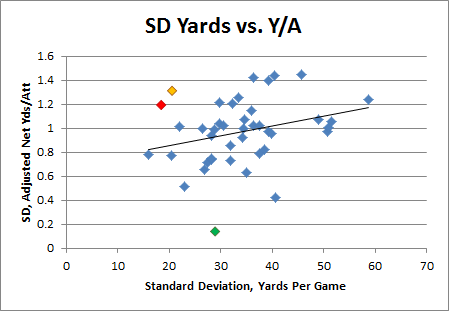
6:20: Sorry, was looking at something completely new to me. Not sure exactly what to make of it, but it’s interesting:
This is QB’s with 7+ seasons of 8+ games who averaged 200+ yards per game (n=42). These are their standard deviations, from season to season (counting only the 8+ gm years), for Yards per Game vs. Adjusted Net Yards Per Attempt.
The red dot is our absentee superstar, Peyton Manning, and the green is Johnny Unitas. The orange is Randall Cunningham, but his numbers I think are skewed a bit because of the Randy Moss effect. The dot at the far left of the trend-line is Jim Kelly.
6:28: So what to make of it? I’ve been mildy critical of Adjusted Net Yards Per Attempt for the same reasons I’ve been critical of Win Percentage Added: Since the QB is involved in basically every offensive play, both of these tend to track two things: 1) Their raw offensive quality, plus (or multiplied by) 2) The amount which the team relies on the passing game. Neither is particularly indicative of a QB doing the best with what he can, as it is literally impossible to put up good numbers in these stats on a bad team.
So it’s interesting to me that Peyton — who most would agree is one of the most consistent QB’s in football — would have such a high ANY/A standard dev (he also has a larger sample than some of the other qualifiers).
6:35: An incredibly superficial interpretation might be that Peyton sacrifices efficiency in order to “get his yards.” OTOH, this may be counter-intuitive, but I wonder if it’s not actually the opposite: Peyton was an extremely consistent winner. Is it possible that the ANY/A to some extent reflected the quality of his supporting cast, but the yards sort of indirectly reflect his ability to transfer whatever he had into actual production? Obv I’d have to think about it more.
6:42: I think when this is over, maybe I should split it into separate parts, roughly grouped by content? Getting unwieldy, but kind of too late to split it now.
7:02: So, according to the commentators, Mike Wallace is now the fastest player in the NFL, which makes him faster than LeSean McCoy, who (as the fastest RB) is faster than Chris Johnson, who (by proclamation) is faster than Usain Bolt, who is the fastest man on the planet. So either someone is an alien (or a neutrino! [sorry, can’t help myself]), or something’s got to give.
7:17: David asks:
Q: The Bills for real? What do they project to over a season?
Um, I don’t know. Generically, being 3-0 and +40 projects to 10 or 11 wins, but there’s a lot of variance in there. The previous season’s results are still fairly significant, as are the million other things most fans could tick off. Another statistically significant factor that most people prob wouldn’t think of is preseason results. The Bills scored 24 and 35 points in games 2 and 3 of the preseason. There’s a ton of work behind this result, but basically I’ve found that points scored plus points scored in games 2 and 3 of the preseason (counting backwards) is approximately as predictive as points scored minus points allowed in one game from the regular season. So, loosely speaking, in this case, you might say that the Bills are more like a 4-0 team, with the extra game worth of data being the equivalent of a fairly quality win over a Denver/Jacksonville Hybrid.
7:27: I’d also note that it’s difficult to take strength of schedule into account at this point, at least in a quantitative way. You can make projections about the quality of a team’s opponents, but the error in those projections are so large at this point that they add more variance to your target team’s projections than they are worth. Or, maybe a simpler way to put it: it’s hard enough to adjust for quality of opponent when you *know* how good they were, and we don’t even know, we just have educated guesses. (Even at the END of the season, I think a lot of ranking models and such don’t sufficiently account for the variance in SoS: that is, when a team beats x number of teams with good records, they can do very well in those rankings, even though some of the teams they beat overperfomed in their other games. In fact, given regression to the mean, this will almost always be the case. Of course, a clever enough model should account for this uncertainty.)
7:28: Man, that was a seriously ramble-y answer to a simple question.
7:44: I remember Mike Wallace being a valuable backup on my fantasy team in 2009, otherwise, meh. Seems to talk a lot of crap that these announcers eat up. Ironically, though, if a rookie or a complete unknown starts a season super-hot, commentary is usually that they’re already the next big thing, while a quality-but-not-superstar veteran with a hot start is often just credited with a hot start. But, in reality, I think the vet, despite being more of a known quantity, is still more likely to take off. In this case, they’re busting out the hyperbole regardless.
8:03: Speaking of which, does anyone remember Ryan Moats? A stringer for Houston in 2009, he ended up starting (briefly) after a rash of injuries to his teammates. In his first start (against Buffalo), he had 150 yards and 3 touchdowns, and some fantasy contestants were falling over each other to pick him up. After that, he had 2 touchdowns the rest of the season, and then was out of football.
8:07: Polamalu to the rescue, of course. He’s so good that I think he improves the Steeler’s offense. (And no, not kidding.)
8:13: So, with Sunday Ticket’s streaming content, instead of watching Monday Night Football, I could watch several whole games instead.
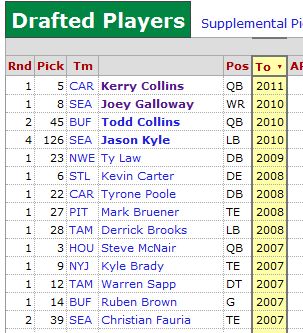
8:20: So I always think of Kerry Collins as a pretty bad QB, but damn: he’s the last man standing from the entire 1995 draft:
And, you know, he’s not dead. So I guess he won that rivalry.
8:25: Oooh, depending on the time out situation, that might have been a spot where dropping just short of the first down would have been better than making it. Too bad Burke’s WPA Calculator doesn’t factor in time outs!
8:31: So before this is over, one more fun fact about Usain Bolt: In his 100M record run, he maintained a minimum speed over a 40 meter stretch that no other man has ever achieved over 10.
8:32: CC just said kickers prefer being on the left hash. [Though the justification was kind of weak.]
8:35: Congrats Steelers, and condolences to Colts fans. With their schedule, Indy may be eliminated from playoff contention before Manning even starts thinking about a return. Could be good for them next year, though: San Antonio Gambit, anyone?
8:38: No Post Game Show for me. Peace out, y’all.
8:59: Okay, one last thought: In this post, Brian Burke estimates Manning’s worth to that team, and uses the team’s total offensive WPA as a sort of “ceiling” for how valuable Manning could be:
In this case, it can tell us how many wins the Peyton Manning passing game can account for. Although we can’t really separate Manning from his blockers and receivers, we can nail down a hard number for the Colts passing game as a whole, of which Manning has been the central fixture.
The analysis, while perfectly good, does ignore two possibilities: First, the Indianapolis offense minus Manning may be below average (negative WPA), in which case the “Colts passing game” as a whole would understate Manning’s value: E.g., he could be taking it from -1 to +2.5, such that he’s actually worth 3.5, etc. Second, even if you could get a proper measure of how much the offense would suffer without Manning, that still may not account for the degree to which the Indianapolis offense bolstered their defense’s stats. When you’re ahead a lot, you force the other team to make sub-optimal plays that increase variance to give themselves some opportunity to catch up: this makes your defense look good. In such a scenario, I would imagine hearing things like, “Oh, the Indianapolis defense is so opportunistic!” Hmmm.