Don’t Play Baseball With Bill Belichick

[Note: I apologize for missing last Wednesday and Friday in my posting schedule. I had some important business-y things going on Wed and then went to Canada for a wedding over the weekend.]

Last week I came across this ESPN article (citing this Forbes article) about how Bill Belichick is the highest-paid coach in American sports:

Bill Belichick tops the list for the second year in a row following the retirement of Phil Jackson, the only coach to have ever made an eight-figure salary. Belichick is believed to make $7.5 million per year. Doc Rivers is the highest-paid NBA coach at $7 million.

Congrats to Belichick for a worthy accomplishment! Though I still think it probably under-states his actual value, at least relative to NFL players. As I tweeted:

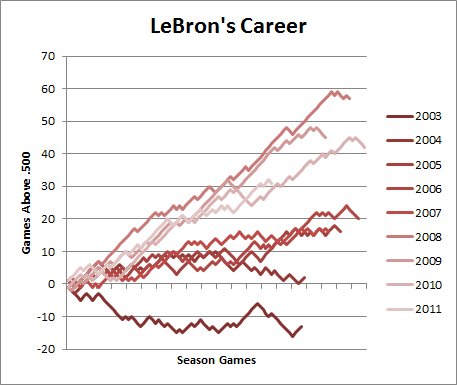
Of course, coaches’ salaries are different from players’: they aren’t constrained by the salary cap, nor are they boosted by the mandatory revenue-sharing in the players’ collective bargaining agreement.  Yet, for comparison, this season Belichick will make a bit more than a third of what Peyton Manning will in Denver. As I’ve said before, I think Belichick and Manning have been (almost indisputably) the most powerful forces in the modern NFL (maybe ever). Here’s the key visual from my earlier post, updated to include last season (press play):

The x axis is wins in season n, y axis is wins in season n+1.

Naturally, Belichick has benefited from having Tom Brady on his team. However, Brady makes about twice as much as Belichick does, and I think you would be hard-pressed to argue that he’s twice as valuable—and I think top QB’s are probably underpaid relative to their value anyway.

But being high on Bill Belichick is about more than just his results. He is well-loved in the analytical community, particularly for some of his high-profile 4th down and other in-game tactical decisions.  But I think those flashy calls are merely a symptom of his broader commitment to making intelligent win-maximizing decisions—a commitment that is probably even more evident in the decisions he has made and strategies he has pursued in his role as the Patriots’ General Manager.

But rather than sorting through everything Belichick has done that I like, I want to take a quick look at one recent adjustment that really impressed me: the Patriots out-of-character machinations in the 2012 draft.

The New Rookie Salary Structure

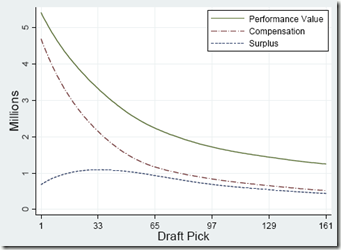
One of the unheralded elements to the Patriots’ success—perhaps rivaling Tom Brady himself in actual importance—is their penchant for stock-piling draft-picks in the “sweet spot” of the NFL draft (late 1st to mid-2nd round), where picks have the most surplus value. Once again, here’s the killer graph from the famous Massey-Thaler study on the topic:

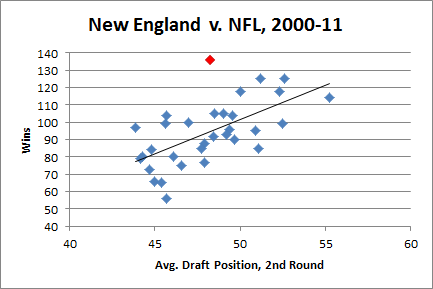
In the 11 drafts since Belichick took over, the Patriots have made 17 picks between numbers 20 and 50 overall, the most in the NFL (the next-most is SF with 15, league average is obv 11). To illustrate how unusual their draft strategy has been, here’s a plot of their 2nd round draft position vs. their total wins over the same period:

Despite New England having the highest win percentage (not to mention most Super Bowl wins and appearances) over the period, there are 15 teams with lower average draft positions in the 2nd round. For comparison, they have the 2nd lowest average draft position in the 1st round and 7th lowest in the third.

Of course, the new collective bargaining agreement includes a rookie salary scale. Without going into all the details (in part because they’re extremely complicated and not entirely public), the key points are that it keeps total rookie compensation relatively stable while flattening the scale at the top, reducing guaranteed money, and shortening the maximum number of years for each deal.

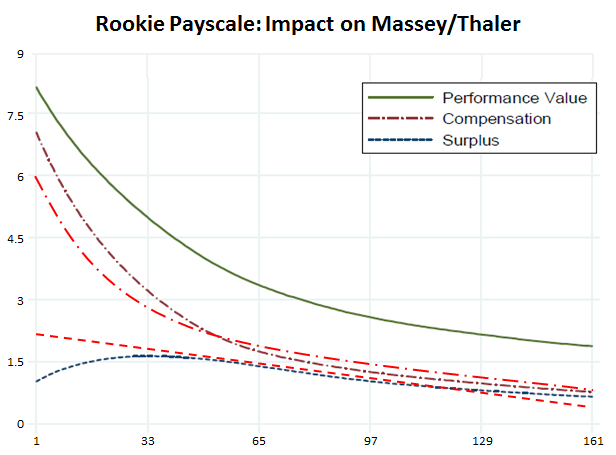
These changes should all theoretically flatten out the “value curve” above. Here’s a rough sketch of what the changes seem to be attempting:

Since the original study was published, the dollar values have gone up and the top end has gotten more skewed. I adjusted the Y-axis to reflect the new top, but didn’t adjust the curve itself, so it should actually be somewhat steeper than it appears.  I tried to make the new curves as conceptually accurate as I could, but they’re not empirical and should be considered more of an “artist’s rendition” of what I think the NFL is aiming for.

With a couple of years of data, this should be a very interesting issue to revisit.  But, for now, I think it’s unlikely that the curve will actually be flattened very much. If I had to guess, I think it may end up “dual-peaked”: By far the greatest drop in guaranteed money will be for top QB prospects taken with the first few picks. These players already provide the most value, and are the main reason the original M/T performance graph inclines so steeply on the left. Additionally, they provide an opportunity for continued surplus value beyond the length of the initial contract. This should make the top of the draft extremely attractive, at least in years with top QB prospects.

On the other hand, I think the bulk of the effect on the rest of the surplus-value curve will be to shift it to the left. My reasons for thinking this are much more complicated, and include my belief that the original Massey/Thaler study has problems with its valuation model, but the extremely short version is that I have reason to believe that people systematically overvalue upper/middle 1st round picks.

How the Patriots Responded

Since I’ve been following the Patriots’ 2nd-round-oriented drafting strategy for years now, naturally my first thoughts after seeing the details of the new deal went to how this could kill their edge. Here’s a question I tweeted at the Sloan conference:

Actually, my concern about the Patriots drafting strategy was two-fold:

  1. The Patriots favorite place to draft could obviously lose its comparative value under the new system. If they left their strategy as-is, it could lead to their picking sub-optimally. At the very least, it should eliminate their exploitation opportunity.
  2. Though a secondary issue for this post, at some point  taking an extreme bang-for-your-buck approach to player value can run into diminishing returns and cause stagnation. Since you can only have so many players on your roster or on the field at a time, your ability to hoard and exploit “cheap” talent is constrained. This is a particularly big concern for teams that are already pretty good, especially if they already have good “value” players in a lot of positions: At some point, you need players who are less cheap but higher quality, even if their value per dollar is lower than the alternative.

Of course, if you followed the draft, you know that the Patriots, entering the draft with far fewer picks than usual, still traded up in the 1st round, twice.

Taken out of context, these moves seem extremely out of character for the Patriots. Yet the moves are perfectly consistent with an approach that understands and attacks my concerns: Making fewer, higher-quality picks is essentially the correct solution, and if the value-curve has indeed shifted up as I expect it has, the new epicenter of the Patriots’ draft activity may be directly on top of the new sweet spot.

Baseball

The entire affair reminds me of an old piece of poker wisdom that goes something like this: In a mixed game with one truly expert poker player and a bunch of completely outclassed amateurs, the expert’s biggest edge wouldn’t come in the poker variant with which he has the most expertise, but in some ridiculous spontaneous variant with tons of complicated made-up rules.

I forget where I first read the concept, but I know it has been addressed in various ways by many authors, ranging from Mike Caro to David Sklansky. I believe it was the latter (though please correct me if I’m wrong), who specifically suggested a Stud variant some of us remember fondly from childhood:

Several different games played only in low-stakes home games are called Baseball, and generally involve many wild cards (often 3s and 9s), paying the pot for wild cards, being dealt an extra upcard upon receiving a 4, and many other ad-hoc rules (for example, the appearance of the queen of spades is called a “rainout” and ends the hand, or that either red 7 dealt face-up is a rainout, but if one player has both red 7s in the hole, that outranks everything, even a 5 of a kind). These same rules can be applied to no peek, in which case the game is called “night baseball”.

The main ideas are that A) the expert would be able to adapt to the new rules much more quickly, and B) all those complicated rules make it much more likely that he would be able to find profitable exploitations (for Baseball in particular, there’s the added virtue of having several betting rounds per hand).

It will take a while to see how this plays out, and of course the abnormal outcome could just be a circumstances-driven coincidence rather than an explicit shift in the Patriots’ approach. But if my intuitions about the situation are right, Belichick may deserve extra credit for making deft adjustments in a changing landscape, much as you would expect from the Baseball-playing shark.

The Clock: A Graph and Some Thoughts

If you’re a hardcore follower of this blog, you know that one of things I have frequently complained about is the failure of NBA play-by-play data to include the shot clock. It’s so obviously important and—relative to other play-by-play data—so easy to track, that it’s a complete mystery to me why doing so isn’t completely standard. OTOH, I see stats broken down by “early” and “late” in the shot clock all the time, so someone must have this information.

In the meantime, I went through the 2010 play-by-play dataset and kluged a proxy stat from the actual clock, reflecting the number of seconds passed since a team took possession. Here’s a chart summarizing the number and outcomes of possessions of various lengths:

The orange X’s represent the number of league-wide possessions in which the first shot took place at the indicated time. The red diamonds represent the average number of points scored on those possessions (including from any subsequent shots following an offensive rebound, etc).

We should expect there to be a constant trade-off at any given time between taking a shot “now” and waiting for a better one to open up: the deeper you get into a possession, the more your shot standards should drop. And, indeed, this is reflected in the graph by the downward-sloping curve.

For now, I’m just throwing this out there. Though it represents a very basic idea, it is difficult to overstate its importance:

  1. Accounting for the clock can help evaluate players where standard efficiency ratings break down. Most simply, you can take the results of each shot and compare them to the expected value of a shot taken under the same amount of time-pressure. E.g., if someone averages .9 points per attempt with only a couple of seconds left, you can spot value where normal efficiency calculations wouldn’t.
  2. Actually, I’ve calculated just such preliminary “value-added” shooting for the entire league (with pretty interesting results), but I’d like to see more accurate data before posting or basing any substantial analysis on it. Among other problems, I think the right side of the curve is overly generous, as it includes possessions where it took a while to get the clock started (a process that is, unfortunately, highly variable), or where time was added and the cause wasn’t scored (also disappointingly common).
  3. Examining this information can tell you some things about the league generally: For example, it’s interesting to me that there’s a noticeable dip right around where the most shots actually take place (14 to 16 seconds in). Though speculative, I suspect that this is when players are most likely to settle for mediocre 2 point jumpers. Similarly, but a bit more difficultly, you can compare the actual curve with a derived curve to examine whether NBA players, on the whole, seem to wait too long (or not long enough) to pull the trigger.

With better data, the possibilities would open up further (even moreso when combined with other play-by-play information, like shot type, position, defense, etc). For example, you could look at the curve for individual players and impute whether they should be more or less aggressive with their shot selection.

So, yeah, if any of you can direct me to a dataset that has what I want, please let me know.

Sports Geek Mecca: Recap and Thoughts, Part 2

This is part 2 of my “recap” of the Sloan Sports Analytics Conference that I attended in March (part 1 is here), mostly covering Day 2 of the event, but also featuring my petty way-too-long rant about Bill James (which I’ve moved to the end).

Day Two

First I attended the Football Analytics despite finding it disappointing last year, and, alas, it wasn’t any better. Eric Mangini must be the only former NFL coach willing to attend, b/c they keep bringing him back:

Overall, I spent more time in day 2 going to niche panels, research paper presentations and talking to people.

The last, in particular, was great. For example, I had a fun conversation with Henry Abbott about Kobe Bryant’s lack of “clutch.” This is one of Abbott’s pet issues, and I admit he makes a good case, particularly that the Lakers are net losers in “clutch” situations (yes, relative to other teams), even over the periods where they have been dominant otherwise.

Kobe is kind of a pivotal case in analytics, I think. First, I’m a big believer in “Count the Rings, Son” analysis: That is, leading a team to multiple championships is really hard, and only really great players do it. I also think he stands at a kind of nexus, in that stats like PER give spray shooters like him an unfair advantage, but more finely tuned advanced metrics probably over-punish the same. Part of the burden of Kobe’s role is that he has to take a lot of bad shots—the relevant question is how good he is at his job.

Abbott also mentioned that he liked one of my tweets, but didn’t know if he could retweet the non-family-friendly “WTF”:

I also had a fun conversation with Neil Paine of Basketball Reference. He seemed like a very smart guy, but this may be attributable to the fact that we seemed to be on the same page about so many things. Additionally, we discussed a very fun hypo: How far back in time would you have to go for the Charlotte Bobcats to be the odds-on favorites to win the NBA Championship?

As for the “sideshow” panels, they’re generally more fruitful and interesting than the ESPN-moderated super-panels, but they offer fewer easy targets for easy blog-griping. If you’re really interested in what went down, there is a ton of info at the SSAC website. The agenda can be found here. Information on the speakers is here. And, most importantly, videos of the various panels can be found here.

Box Score Rebooted

Featuring Dean Oliver, Bill James, and others.

This was a somewhat interesting, though I think slightly off-target, panel. They spent a lot of time talking about new data and metrics and pooh-poohing things like RBI (and even OPS), and the brave new world of play-by-play and video tracking, etc. But too much of this was discussing a different granularity of data than what can be improved in the current granularity levels. Or, in other words:

James acquitted himself a bit on this subject, arguing that boatloads of new data isn’t useful if it isn’t boiled down into useful metrics. But a more general way of looking at this is: If we were starting over from scratch, with a box-score-sized space to report a statistical game summary, and a similar degree of game-scoring resources, what kinds of things would we want to include (or not) that are different from what we have now?  I can think of a few:

  1. In basketball, it’s archaic that free-throws aren’t broken down into bonus free throws and shot-replacing free throws.
  2. In football, I’d like to see passing stats by down and distance, or at least in a few key categories like 3rd and long.
  3. In baseball, I’d like to see “runs relative to par” for pitchers (though this can be computed easily enough from existing box scores).

In this panel, Dean Oliver took the opportunity to plug ESPN’s bizarre proprietary Total Quarterback Rating. They actually had another panel devoted just to this topic, but I didn’t go, so I’ll put a couple of thoughts here.

First, I don’t understand why ESPN is pushing this as a proprietary stat. Sure, no-one knows how to calculate regular old-fashioned quarterback ratings, but there’s a certain comfort in at least knowing it’s a real thing. It’s a bit like Terms of Service agreements, which people regularly sign without reading: at least you know the terms are out there, so someone actually cares enough to read them, and presumably they would raise a stink if you had to sign away your soul.

As for what we do know, I may write more on this come football season, but I have a couple of problems:

One, I hate the “clutch effect.” TQBR makes a special adjustment to value clutch performance even more than its generic contribution to winning. If anything, clutch situations in football are so bizarre that they should count less. In fact, when I’ve done NFL analysis, I’ve often just cut the 4th quarter entirely, and I’ve found I get better results. That may sound crazy, but it’s a bit like how some very advanced Soccer analysts have cut goal-scoring from their models, instead just focusing on how well a player advances the ball toward his goal: even if the former matters more, its unreliability may make it less useful.

Two, I’m disappointed in the way they “assign credit” for play outcomes:

Division of credit is the next step. Dividing credit among teammates is one of the most difficult but important aspects of sports. Teammates rely upon each other and, as the cliché goes, a team might not be the sum of its parts. By dividing credit, we are forcing the parts to sum up to the team, understanding the limitations but knowing that it is the best way statistically for the rating.

I’m personally very interested in this topic (and have discussed it with various ESPN analytics guys since long before TQBR was released). This is basically an attempt to address the entanglement problem that permeates football statistics.  ESPN’s published explanation is pretty cryptic, and it didn’t seem clear to me whether they were profiling individual players and situations or had created credit-distribution algorithms league-wide.

At the conference, I had a chance to talk with their analytics guy who designed this part of the metric (his name escapes me), and I confirmed that they modeled credit distribution for the entire league and are applying it in a blanket way.  Technically, I guess this is a step in the right direction, but it’s purely a reduction of noise and doesn’t address the real issue.  What I’d really like to see is like a recursive model that imputes how much credit various players deserve broadly, then uses those numbers to re-assign credit for particular outcomes (rinse and repeat).

Deconstructing the Rebound With Optical Tracking Data

Rajiv Maheswaran, and other nerds.

This presentation was so awesome that I offered them a hedge bet for the “Best Research Paper” award. That is, I would bet on them at even money, so that if they lost, at least they would receive a consolation prize. They declined. And won. Their findings are too numerous and interesting to list, so you should really check it out for yourself.

Obviously my work on the Dennis Rodman mystery makes me particularly interested in their theories of why certain players get more rebounds than others, as I tweeted in this insta-hypothesis:

Following the presentation, I got the chance to talk with Rajiv for quite a while, which was amazing. Obviously they don’t have any data on Dennis Rodman directly, but Rajiv was also interested in him and had watched a lot of Rodman video. Though anecdotal, he did say that his observations somewhat confirmed the theory that a big part of Rodman’s rebounding advantage seemed to come from handling space very well:

  1. Even when away from the basket, Rodman typically moved to the open space immediately following a shot. This is a bit different from how people often think about rebounding as aggressively attacking the ball (or as being able to near-psychically predict where the ball is going to come down.
  2. Also rather than simply attacking the board directly, Rodman’s first inclination was to insert himself between the nearest opponent and the basket. In theory, this might slightly decrease the chances of getting the ball when it heads in toward his previous position, but would make up for it by dramatically increasing his chances of getting the ball when it went toward the other guy.
  3. Though a little less purely strategical, Rajiv also thought that Rodman was just incredibly good at #2. That is, he was just exceptionally good at jockeying for position.

To some extent, I guess this is just rebounding fundamentals, but I still think it’s very interesting to think about the indirect probabilistic side of the rebounding game.

Live B.S. Report with Bill James

Quick tangent: At one point, I thought Neil Paine summed me up pretty well as a “contrarian to the contrarians.”  Of course, I’m don’t think I’m contrary for the sake of contrariness, or that I’m a negative person (I don’t know how many times I’ve explained to my wife that just because I hated a movie doesn’t mean I didn’t enjoy it!), it’s just that my mind is naturally inclined toward considering the limitations of whatever is put in front of it. Sometimes that means criticizing the status quo, and sometimes that means criticizing its critics.

So, with that in mind, I thought Bill James’s showing at the conference was pretty disappointing, particularly his interview with Bill Simmons.

I have a lot of respect for James.  I read his Historical Baseball Abstract and enjoyed it considerably more than Moneyball.  He has a very intuitive and logical mind. He doesn’t say a bunch of shit that’s not true, and he sees beyond the obvious. In Saturday’s “Rebooting the Box-score” panel, he made an observation that having 3 of 5 people on the panel named John implied that the panel was [likely] older than the rest of the room.  This got a nice laugh from the attendees, but I don’t think he was kidding.  And whether he was or not, he still gets 10 kudos from me for making the closest thing to a Bayesian argument I heard all weekend.  And I dutifully snuck in for a pic with him:

James was somewhat ahead of his time, and perhaps he’s still one of the better sports analytic minds out there, but in this interview we didn’t really get to hear him analyze anything, you know, sportsy. This interview was all about Bill James and his bio and how awesome he was and how great he is and how hard it was for him to get recognized and how much he has changed the game and how, without him, the world would be a cold, dark place where ignorance reigned and nobody had ever heard of “win maximization.”

Bill Simmons going this route in a podcast interview doesn’t surprise me: his audience is obviously much broader than the geeks in the room, and Simmons knows his audience’s expectations better than anyone. What got to me was James’s willingness to play along, and everyone else’s willingness to eat it up. Here’s an example of both, from the conference’s official Twitter account:

Perhaps it’s because I never really liked baseball, and I didn’t really know anyone did any of this stuff until recently, but I’m pretty certain that Bill James had virtually zero impact on my own development as a sports data-cruncher.  When I made my first PRABS-style basketball formula in the early 1990’s (which was absolutely terrible, but is still more predictive than PER), I had no idea that any sports stats other than the box score even existed. By the time I first heard the word “sabermetrics,” I was deep into my own research, and didn’t bother really looking into it deeply until maybe a few months ago.

Which is not to say I had no guidance or inspiration.  For me, a big epiphanous turning point in my approach to the analysis of games did take place—after I read David Sklansky’s Theory of Poker. While ToP itself was published in 1994, Sklansky’s similar offerings date back to the 70s, so I don’t think any broader causal pictures are possible.

More broadly, I think the claim that sports analytics wouldn’t have developed without Bill James is preposterous. Especially if, as i assume we do, we firmly believe we’re right.  This isn’t like L. Ron Hubbard and Incident II: being for sports analytics isn’t like having faith in a person or his religion. It simply means trying to think more rigorously about sports, and using all of the available analytical techniques we can to gain an advantage. Eventually, those who embrace the right will win out, as we’ve seen begin to happen in sports, and as has already happened in nearly every other discipline.

Indeed, by his own admission, James liked to stir controversy, piss people off, and talk down to the old guard whenever possible. As far as we know, he may have set the cause of sports analytics back, either by alienating the people who could have helped it gain acceptance, or by setting an arrogant and confrontational tone for his disciples (e.g., the uplifting “don’t feel the need to explain yourself” message in Moneyball). I’m not saying that this is the case or even a likely possibility, I’m just trying to illustrate that giving someone credit for all that follows—even a pioneer like James—is a dicey game that I’d rather not participate in, and that he definitely shouldn’t.

On a more technical note, one of his oft-quoted and re-tweeted pearls of wisdom goes as follows:

Sounds great, right? I mean, not really, I don’t get the metaphor: if the sea is full of ignorance, why are you collecting water from it with a bucket rather than some kind of filtration system? But more importantly, his argument in defense of this claim is amazingly weak. When Simmons asked what kinds of things he’s talking about, he repeatedly emphasized that we have no idea whether a college sophomore will turn out to be a great Major League pitcher.  True, but, um, we never will. There are too many variables, the input and outputs are too far apart in time, and the contexts are too different.  This isn’t the sea of ignorance, it’s a sea of unknowns.

Which gets at one of my big complaints about stats-types generally.  A lot of people seem to think that stats are all about making exciting discoveries and answering questions that were previously unanswerable. Yes, sometimes you get lucky and uncover some relationship that leads to a killer new strategy or to some game-altering new dynamic. But most of the time, you’ll find static. A good statistical thinker doesn’t try to reject the static, but tries to understand it: Figuring out what you can’t know is just as important as figuring out what you can know.

On Twitter I used this analogy:

Success comes with knowing more true things and fewer false things than the other guy.

Graphs of the Day: Bird vs. Bron

One of my favorite stat-nuggets ever is that “Larry Bird never had a losing month.” So, yesterday, I figured it was about time to check whether or not it’s, you know, true.

To do this, I first had to figure out which Celtics games Bird actually played in. The problem there is that his career began well before 1986, meaning the box score data aren’t in Basketball Reference’s database. But they do have images of the actual box scores, like so:

Fortunately, Bird played in every game in his first two seasons, so figuring this out was just a matter of poring through 4 years of these pics: Easy peasy! (I’ve done more grueling work for even more trivial questions, to be sure.) But results on that later.

Independently, I was trying to come up with a fun way to illustrate the fact that LeBron James won a lot more games in his last two seasons on the lowly Cleveland Cavaliers than he has so far on the perma-hyped Miami Heat:

So that graph reflects every game of LeBron’s career, including the regular season and playoffs (through last night). It’s pretty straightforward: With LeBron an 18-year-old rookie, the Cavs (though much improved) were still pretty shaky, and they pretty much got better and better each year. After a slight decline from their soaring 2008 performance, LeBron left to join the latest Big 3—which is a solid contender, but no threat to the greatest Big 3. (BTW, I would like to thank the Heat for becoming Exhibit A for my long-time contention that having multiple “primary” options is less valuable than having a well-designed supporting cast—even one with considerably less talent.)

But with Mr. Trifecta on my mind (not to mention overloading my browser history), I thought it might be fun to compare the two leading contenders for the small forward spot on any NBA GOAT team. So here’s Larry:

Wow, pretty crazy consistent, yes? Keep in mind that, despite the Celtics long winning tradition, they only won 29 games the year before Bird’s arrival.  Note the practically opposite gradient from LeBron’s: Bird started out hot, and basically stayed hot until injuries cooled him down.

As for the results of the original inquiry: It turns out Bird’s Celtics started the season 2-4 in November 1988, just before Bird had season-ending ankle surgery (of course, Bird’s 1988 games ARE in my database, so this was a bit of a “Doh!” finding). And, of course, he also had losing months in the playoffs.

His worst full month in the regular season, however, was indeed exactly .500: He went 8-8 in March of 1982. So, properly qualified (like, “In the regular season, Bird never had a losing month in which he played more than 6 games”), the claim holds up. If I were a political fact-checker, I would deem it “Mostly True.”

In case you’re interested, here is the complete list of months in Larry Bird’s career:

[table “10” not found /]

The Case Against the Case for Dennis Rodman: Initial Volleys

When I began writing about Dennis Rodman, I was so terrified that I would miss something and the whole argument would come crashing down that I kept pushing it further and further and further, until a piece I initially planned to be about 10 pages of material ended up being more like 150. [BTW, this whole post may be a bit too inside-baseball if you haven’t actually read—or at least skimmed—my original “Case for Dennis Rodman.” If so, that link has a helpful guide.]

The downside of this, I assumed, is that the extra material should open up many angles of attack. It was a conscious trade-off, knowing that individual parts in the argument would be more vulnerable, but the Case as a whole would be thorough and redundant enough to survive any battles I might end up losing.

Ultimately, however, I’ve been a bit disappointed in the critical response. Most reactions I’ve seen have been either extremely complimentary or extremely dismissive.

So a while ago, I decided that if no one really wanted to take on the task, I would do it myself. In one of the Rodman posts, I wrote:

Give me an academic who creates an interesting and meaningful model, and then immediately devotes their best efforts to tearing it apart!

And thus The Case Against the Case for Dennis Rodman is born.

Before starting, here are a few qualifying points:

  1. I’m not a lawyer, so I have no intention of arguing things I don’t believe. I’m calling this “The Case Against the Case For Dennis Rodman,” because I cannot in good faith (barring some new evidence or argument I am as yet unfamiliar with) write The Case Against Dennis Rodman.
  2. Similarly, where I think an argument is worth being raised and discussed but ultimately fails, I will make the defense immediately (much like “Objections and Replies”).
  3. I don’t have an over-arching anti-Case hypothesis to prove, so don’t expect this series to be a systematic takedown of the entire enterprise. Rather, I will point out weaknesses as I consider them, so they may not come in any kind of predictable order.
  4. If you were paying attention, of course you noticed that The Case For Dennis Rodman was really (or at least concurrently) about demonstrating how player valuation is much more dynamic and complicated than either conventional or unconventional wisdom gives it credit for. But, for now, The Case Against the Case will focus mainly on the Dennis Rodman part.

Ok, so with this mission in mind, let me start with a bit of what’s out there already:

A Not-Completely-Stupid Forum Discussion

I admit, I spend a fair amount of time following back links to my blog. Some of that is just ego-surfing, but I’m also desperate to find worthy counter-arguments.

As I said above, that search is sometimes more fruitless than I would like. Even the more intelligent discussions usually include a lot of uninspired drivel. For example, let’s look at a recent thread on RealGM. After one person lays out a decent (though imperfect) summary of my argument, there are several responses along the lines of poster “SVictor”s:

I won’t pay attention to any study that states that [Rodman might be more valuable than Michael Jordan].

Actually, I’m pretty sympathetic to this kind of objection. There can be a bayesian ring of truth to “that is just absurd on its face” arguments (I once made a similar argument against an advanced NFL stat after it claimed Neil O’Donnell was the best QB in football). However, it’s not really a counter-argument, it’s more a meta-argument, and I think I’ve considered most of those to death. Besides, I don’t actually make the claim in question, I merely suggest it as something worth considering.

A much more detailed and interesting response comes from poster “mysticbb.” Now, he starts out pretty insultingly:

The argumentation is biased, it is pretty obvious, which makes it really sad, because I know how much effort someone has to put into such analysis.

I cannot say affirmatively that I have no biases, or that bias never affects my work. Study after study shows that this is virtually impossible. But I can say that I am completely and fundamentally committed to identifying it and stamping it out wherever I can. So, please—as I asked in my conclusion—please point out where the bias is evident and I will do everything in my power to fix it.

Oddly, though, mysticbb seems to endorse (almost verbatim) the proposition that I set out to prove:

Let me start with saying that Dennis Rodman seems to be underrated by a lot of people. He was a great player and deserved to be in the HOF, I have no doubt about that. He had great impact on the game and really improved his team while playing.

(People get so easily distracted: You write one article about a role-player maybe being better than Michael Jordan, and they forget that your overall claim is more modest.)

Of course, my analysis could just be way off, particularly in ways that favor Rodman. To that end, mysticbb raises several valid points, though with various degrees of significance.

Here he is on Rodman’s rebounding:

Let me start with the rebounding aspect. From 1991 to 1998 Rodman was leading the league in TRB% in each season. He had 17.7 ORB%, 33 DRB% and overall 25.4 TRB%. Those are AWESOME numbers, if we ignore context. Let us take a look at the numbers for the playoffs during the same timespan: 15.9 ORB%, 27.6 DRB% and 21.6 TRB%. Still great numbers, but obviously clearly worse than his regular season numbers. Why? Well, Rodman had the tendency to pad his rebounding stats in the regular season against weaker teams, while ignoring defensive assignments and fighting his teammates for rebounds. All that was eliminated during the playoffs and his numbers took a hit.

Now, I don’t know how much I talked about the playoffs per se, but I definitely discussed—and even argued myself—that Rodman’s rebounding numbers are likely inflated. But I also argued that if that IS the case, it probably means Rodman was even more valuable overall (see that same link for more detail). He continues:

Especially when we look at the defensive rebounding part, during the regular season he is clearly ahead of Duncan or Garnett, but in the playoffs they are all basically tied. Now imagine, Rodman brings his value via rebounding, what does that say about him, if that value is matched by players like Duncan or Garnett who both are also great defenders and obviously clearly better offensive players?

Now, as I noted at the outset Rodman’s career offensive rebounding percentage is approximately equal to Kevin Garnett’s career overall rebounding percentage, so I think Mystic is making a false equivalency based on a few cherry-picked stats.

But, for a moment, let’s assume it were true that Garnett/Duncan had similar rebounding numbers to Rodman, so what? Rodman’s crazy rebounding numbers cohere nicely with the rest of the puzzle as an explanation of why he was so valuable—his absurd rebounding stats make his absurd impact stats more plausible and vice versa—but they’re technically incidental. Indeed, they’re even incidental to his rebounding contribution: The number (or even percent) of rebounds a player gets does not correlate very strongly with the number of rebounds he has actually added to his team (nor does a player’s offensive “production” correlate very strongly with improvement in a team’s offense), and it does so the most on the extremes.

But I give the objection credit in this regard: The playoff/regular season disparity in Rodman’s rebounding numbers (though let’s not overstate the case, Rodman has 3 of the top 4 TRB%’s in playoff history) do serve to highlight how dynamic basketball statistics are. The original Case For Dennis Rodman is perhaps too willing to draw straight causal lines, and that may be worth looking into. Also, a more thorough examination of Rodman’s playoff performance may be in order as well.

On the indirect side of The Case, mysticbb has this to say:

[T]he high difference between the team performance in games with Rodman and without Rodman is also caused by a difference in terms of strength of schedule, HCA and other injured players.

I definitely agree that my crude calculation of Win % differentials does not control for a number of things that could be giving Rodman, or any other player, a boost. Controlling for some of these things is probably possible, if more difficult than you might think. This is certainly an area where I would like to implement some more robust comparison methods (and I’m slowly working on it).

But, ultimately, all of the factors mysticbb mentions are noise. Circumstances vary and lots of things happen when players miss games, and there are a lot of players and a lot of circumstances in the sample that Rodman is compared to: everyone has a chance to get lucky. That chance is reflected in my statistical significance calculations.

Mysticbb makes some assertions about Rodman having a particularly favorable schedule, but cites only the 1997 Bulls, and it’s pretty thin gruel:

If we look at the 12 games with Kukoc instead of Rodman we are getting 11.0 SRS. So, Rodman over Kukoc made about 0.5 points.

Of course, if there is evidence that Rodman was especially lucky over his career, I would like to see it. But, hmm, since I’m working on the Case Against myself, I guess that’s my responsibility as well. Fair enough, I’ll look into it.

Finally, mysticbb argues:

The last point which needs to be considered is the offcourt issues Rodman caused, which effected the outcome of games. Take the 1995 Spurs for example, when Rodman refused to guard Horry on the perimeter leading to multiple open 3pt shots for Horry including the later neck-breaker in game 6. The Spurs one year later without Rodman played as good as in 1995 with him.

I don’t really have much to say on the first part of this. As I noted at the outset, there’s some chance that Rodman caused problems on his team, but I feel completely incompetent to judge that sort of thing. But the other part is interesting: It’s true that the Spurs were only 5% worse in 95-96 than they were in 94-95 (OFC, they would be worse measuring only against games Rodman played in), but cross-season comparisons are obviously tricky, for a number of reasons. And if they did exist, I’m not sure they would break the way suggested. For example, the 2nd Bulls 3-peat teams were about as much better than the first Bulls 3-peat as the first Bulls 3-peat was better than the 93-95 teams that were sans Michael Jordan.

That said, I actually do find multi-season comparisons to be a valid area for exploration. So, e.g., I’ve spent some time looking at rookie impact and how predictive it is of future success (answer: probably more than you think).

Finally, a poster named “parapooper” makes some points that he credits to me, including:

He also admits that Rodman actually has a big advantage in this calculation because he missed probably more games than any other player due to reasons other than health and age.

I don’t actually remember making this point, at least this explicitly, but it is a valid concern IMO. A lot of the In/Out numbers my system generated include seasons where players were old or infirm, which disadvantages them. In fact, I initially tried to excise these seasons, and tried accounting for them in a variety of ways, such as comparing “best periods” to “best periods”, etc. But I found such attempts to be pretty unwieldy and arbitrary, and they shrunk the sample size more than I thought they were worth, without affecting the bottom line: Rodman just comes out on top of a smaller pile. That said, some advantage to Rodman relative to others must exist, and quantifying that advantage is a worthy goal.

A similar problem that “para” didn’t mention specifically is that a number of the in/out periods for players include spots where the player was traded. In subsequent analysis, I’ve confirmed what common sense would probably indicate: A player’s differential stats in trade scenarios are much less reliable. Future versions of the differential comparison should account for this, one way or another.

The differential analysis in the series does seem to be the area that most needs upgrading, though the constant trade-off between more information and higher quality information means it will never be as conclusive as we might want it to be. Not mentioned in this thread (that I saw), but what I will certainly deal with myself, are broader objections to the differential comparisons as an enterprise. So, you know. Stay tuned.

Championship Experience Matters! (Super Bowl Edition)

To complete “Championship Week” at Skeptical Sports, I thought I’d post a little fun research I did before this year’s Super Bowl.

Like basketball, teams with championship-winning experience outperform their regular-season records in the playoffs, especially if they make it to the Super Bowl.

So, a bit like my 5-by-5 model, I wanted to come up with a simple metric for picking the Super Bowl winner. Unlike its NBA cousin, however, this method only applies to the championship game, not to the entire playoffs. The main question is, how much better does a team with more Super Bowl winning experience do than it’s opponent?

I feel bad about my text/graphs ratio this week, so I thought I’d tell this story in pictures. Before testing the question, we need to pick the best time period. So, for what number of years does the metric “pick the team with the most super bowl wins” most often pick the ultimate winner:

This was a little surprising to me already: I thought for sure the best n would be a small number, but it turns out to be 6.

Counting 2012, there have been 26 Super Bowls where one team has won more championships in the previous 6 years than the other. Of those games, the team with the greater number has won 20, or 77% of the time—including the Giants. [True story: I was going to publish something on this research before this year’s Super Bowl, but, knowing that it predicted a New York win against the heavily favored Patriots, I chickened out.]

Of course, I’m sure most of you are just itching to pounce right now: Clearly the team with the most recent Super Bowl wins is usually going to be better, right? So clearly this must be confounding this result. So let’s compare it to the predictive accuracy of SRS (Simple Rating System, aka “Margin of Victory adjusted for Strength of Schedule”):

Looking at all 46 Super Bowls, the team with the higher SRS has won 26, or 57%. In Super Bowls where no team had more Super Bowl wins, SRS performs slightly better, correctly picking 12/20 (60%). But the real story is in the games where both had something to say: When SRS and L6 agreed, the team they both picked won 11/14 (79%). But when SRS and L6 disagreed—in other words, where one team had a higher SRS, but the other had more Super Bowl wins in the previous 6 years—the team with the paper qualifications lost to the team with the championship experience 9 of 12 times (75%).

Now, your next thought might be that the years when L6 trumped SRS were probably the years when the teams were very close. But you’d be wrong:

The average SRS difference in 9 years where the L6 team won is actually higher than in the 3 years when it lost!

So how much does L6 add overall? Well, let’s first create a simple method, a bit like 5-by-5:

  1. If one team has more Super Bowl wins in the previous 6 years, pick them.
  2. Otherwise, pick the team with the best SRS.

Following this method, you would correctly pick 32 of the 46 Super Bowls (70%), for a 10% improvement overall, despite step 1 only even applying in about half of the games (also, note that if you just picked randomly in the 20 Super Bowls where L6 doesn’t apply, you would still be expected to get 30 right overall).

Finally, to try to quantify the difference in predictive value between the two measures, I plugged them both into a logistic regression:

As you can see, L6 is much more predictive, though the 95% confidence intervals do overlap. (Though I should also note, this last chart is based on the regression I ran prior to this year’s game, which ended up being another victory for the championship experience side.)

Championship Experience Matters! (Un-Sexy Version)

So in Monday’s post, I included my “5-by-5” method (I probably shouldn’t call it a “model”) for picking NBA champions. In case you missed it, here it is again:

  1. If there are any teams within 5 games of the best record that have won a title within the past 5 years, pick the most recent winner.
  2. Otherwise, pick the team with the best record.

In the 28 seasons since the NBA moved to a 16-team playoff format, this method correctly picked the eventual champion 18 times (64%), comparing favorably to the 10/28 (36%) success rate of the team with the league’s best record.

Henry Abbott blogged about it on ESPN yesterday, raising the obvious follow-up:

The question is, why? Why are teams that have won before so much better at winning again? I’ll kick off the brainstorming:

  • Maybe most teams fall short of their potential because of team dynamics of selfishness — and maybe champions are the teams that know how to move past that.
  • Maybe there are only a few really special coaches, and these teams have them.
  • Maybe there are only a few really special teams, and these teams are them.
  • Maybe there are special strategies to the playoffs that only some teams know. Not even sure what I’m talking about here — Sleep schedules? Nutrition? Injury prevention?
  • Maybe champions get better treatment from referees.

Anyway, it’s certainly fascinating.

UPDATE: John Hollinger with a good point that fits this and other data: Maybe title-winning team don’t value the regular season much.

Though I think some of these ideas are more on point than others, I won’t try to go parse every possibility. On balance, I’m sympathetic to the idea that “winning in the playoffs” has its own skillset independent of just being good at winning basketball games. Conceptually, it’s not too big a leap from the well-documented idea that winning games has its own skillset independent of scoring and allowing points (though the evidence is a lot more indirect).

That said, I think the biggest factor behind this result may be a bit less sexy: It may simply be a matter of information reliability.

Winning Championships is Harder than Winning Games

In stark contrast to other team sports, the NBA Playoffs are extremely deterministic. The best team usually wins (and, conversely, the winner is usually the best team). I’ve made this analogy many times before, but I’ll make it again: The NBA playoffs are a lot more like a Major tournament in men’s tennis than any other crowning competition in popular sports.

This is pretty much a function of design: A moderately better team becomes a huge favorite in a 7 game series. So even if the best team is only moderately better than the 2nd best team, they can be in a dominant position.

Combine this with an uneven distribution of talent (which, incidentally, is probably a function of salary structure), and mix in the empirical reality that the best teams normally don’t change very much from year to year, and its unsurprising that “dynasties” are so common.

On the other side of the equation, regular season standings and leaderboards—whether of wins or its most stable proxies—are highly variable. Note that a 95% confidence interval on an 82 game sample (aka, the “margin of error”) is +/- roughly 10 games.

If you think of the NBA regular season as a lengthy 30-team competition for the #1 seed, its structure is much, much less favorable to the best teams than the playoffs: It’s more like a golf tournament than a tennis tournament.

The Rest is Bayes

Obviously better teams win more often and vice-versa. It’s just that these results have to be interpreted in a context where all results were not equally likely ex ante. For example, the teams who post top records who also have recent championships are far more likely than others to actually be as good as their records indicate. This is pure bayesian inference.

Quick tangent: In my writing, I often reach a point where I say something along the lines of: “From there, it’s all bayesian inference.” I recognize that, for a lot of readers, this is barely a step up from an Underpants Gnomes argument. When I go there, it’s pretty much shorthand for “this is where results inform our beliefs about how likely various causes are to be true” (and all that entails).

There was an interesting comment on Abbott’s ESPN post, pointing out that the 5-by-5 method only picked 5/14 (35.7%) of champions correctly between 1967 and 1980. While there may be unrelated empirical reasons for this, I think this stat may actually confirm the underlying concept. Structurally, having fewer teams in the playoffs, shorter series lengths, a smaller number of teams in the league—basically any of the structural differences between the two eras I can think of—all undermine the combined informational value of [having a championship + having a top record].

To be fair, there may be any number of things in a particular season that undermine our confidence in this inference (I can think of some issues with this season’s inputs, obv). That’s the tricky part of bayesian reasoning: It turns on how plausible you thought things were already.

Stat Geek Smackdown 2012, Round 1: Odds and Ends

So in case any of you haven’t been following, the 2012 edition of the ESPN True Hoop Stat Geek Smackdown  is underway.  Now, obviously this competition shouldn’t be taken too seriously, as it’s roughly the equivalent of picking a weekend’s worth of NFL games, and last year I won only after picking against my actual opinion in the Finals (with good reason, of course).  That said, it’s still a lot of fun to track, and basketball is a deterministic-enough sport that I do think skill is relevant. At least enough that I will talk shit if I win again.

To that end, the first round is going pretty well for me so far.  Like last year, the experts are mostly in agreement. While there is a fair amount of variation in the series length predictions, there are only two matchups that had any dissent as to the likely winner: the 6 actual stat geeks split 4-2 in favor of the Lakers over the Nuggets, and 3-3 between the Clippers and the Grizzlies.  As it happens, I have both Los Angeles teams (yes, I am from Homer), as does Matthew Stahlhut (though my having the Lakers in 5 instead of 7 gives me a slight edge for the moment).  No one has gained any points on anyone else yet, but here is my rough account of possible scenarios:

[table “9” not found /]

On to some odds and ends:

The Particular Challenges of Predicting 2012

Making picks this year was a bit harder than in years past.  At one point I seriously considered picking Dallas against OKC (in part for strategic purposes), before reason got the better of me.  Abbott only published part of my comment on the series, so here’s the full version I sent him:

Throughout NBA history, defending champions have massively over-performed in the playoffs relative to their regular season records, so I wouldn’t count Dallas out.  In fact, the spot Dallas finds itself in is quite similar to Houston’s in 1995, and this season’s short lead -time and compressed schedule should make us particularly wary of the usual battery of predictive models.

Thus, if I had to pick which of these teams is more likely to win the championship, I might take Dallas (or at least it would be a closer call).  But that’s a far different question from who is most likely to win this particular series: Oklahoma City is simply too solid and Dallas too shaky to justify an upset pick. E.g., my generic model makes OKC a >90% favorite, so even a 50:50 chance that Dallas really is the sleeping giant Mark Cuban dreams about probably wouldn’t put them over the top.

That last little bit is important: The “paper gap” between Dallas and OKC is so great that even if Dallas were considerably better than they appeared during the regular season, that would only make them competitive, while if they were about as good as they appeared, they would be a huge dog (this kind of situation should be very familiar to any serious poker players out there).

But why on earth would I think Dallas might be any good in the first place? Well, I’ll discuss more below why champions should never be ignored, but the “paper difference” this year should be particularly inscrutable.  The normal methods for predicting playoff performance (both my own and others) are particularly ill-suited for the peculiar circumstances of this season:

  1. Perhaps most obviously, fewer regular season games means smaller sample sizes.  In turn, this means that sample-sensitive indicators (like regular season statistics) should have less persuasive value relative to non-sensitive ones (like championship pedigree).  It also affects things like head to head record, which is probably more valuable than a lot of stats people think, though less valuable than a lot of non-stats people think.  I’ve been working on some research about this, but for an example, look at this post about how I thought there seemed to be a market error w/r/t Dallas vs. Miami in game 6, partly b/c of the bayesian value of Dallas’s head to head advantage.
  2. Injuries are a bigger factor. This is not just that there are more of them (which is debatable), but there is less flexibility to effectively manage them: e.g., there’s obv less time to rehab players, but also less time to develop new line-ups and workarounds or make other necessary adjustments. In other words, a very good team might be hurt more by a role-player being injured than usual.
  3. What is the most reliable data? Two things I discussed last year were that (contra unconventional wisdom) Win% is more reliable for post-season predictions than MOV-type stats, and that (contra conventional wisdom) early season performance is typically more predictive than late season performance.  But both of these are undermined by the short season.  The fundamental value of MOV is as a proxy for W% that is more accurate for smaller sample sizes. And the predictive power of early-season performance most likely stems from its being more representative of playoff basketball: e.g., players are more rested and everyone tries their hardest.  However, not only are these playoffs not your normal playoffs, but this season was thrown together so quickly that a lot of teams had barely figured out their lineups by the quarter-pole. While late-season records have the same problems as usual, they may be more predictive just from being more similar to years past.
  4. Finally, it’s not just the nature of the data, but the nature of the underlying game as well. For example, in a lockout year, teams concerned with injury may be quicker to pull starting players in less lopsided scenarios than usual, making MOV less useful, etc. I won’t go into every possible difference, but here’s a related Twitter exchange:


Which brings us to the next topic:

The Simplest Playoff Model You’ll Never Beat

The thing that Henry Abbott most highlighted from my Smackdown picks (which he quoted at least 3 times in 3 different places) was my little piece of dicta about the Spurs:

I have a ‘big pot’ playoff model (no matchups, no simulations, just stats and history for each playoff team as input) that produces some quirky results that have historically out-predicted my more conventional models. It currently puts San Antonio above 50 percent. Not just against Utah, but against the field. Not saying I believe it, but there you go.

I really didn’t mean for this to be taken so seriously: it’s just one model.  And no, I’m not going to post it. It’s experimental, and it’s old and needs updating (e.g., I haven’t adjusted it to account for last season yet).

But I can explain why it loves the Spurs so much: it weights championship pedigree very strongly, and the Spurs this year are the only team near the top that has any.

Now some stats-loving people argue that the “has won a championship” variable is unreliable, but I think they are precisely wrong.  Perhaps this will change going forward, but, historically, there are no two ways to cut it: No matter how awesomely designed and complicated your models/simulations are, if you don’t account for championship experience, you will lose to even the most rudimentary model that does.

So case in point, I came up with this 2-step method for picking NBA Champions:

  1. If there are any teams within 5 games of the best record that have won a title within the past 5 years, pick the most recent.
  2. Otherwise, pick the team with the best record.

Following this method, you would correctly pick the eventual NBA Champion in 64.3% of years since the league moved to a 16-team playoff in 1984 (with due respect to the slayer, I call this my “5-by-5” model ).

Of course, thinking back, it seems like picking the winner is sometimes easy, as the league often has an obvious “best team” that is extremely unlikely to ever lose a 7 game series.  So perhaps the better question to ask is: How much do you gain by including the championship test in step 1?

The answer is: a lot. Over the same period, the team with the league’s best record has won only 10/28 championships, or ~35%. So the 5-by-5 model almost doubles your hit rate.

And in case you’re wondering, using Margin of Victory, SRS, or any other advanced stat instead of W-L record doesn’t help: other methods vary from doing slightly worse to slightly better. While there may still be room to beef up the complexity of your predictive model (such as advanced stats, situational simulations, etc), your gains will be (comparatively) marginal at best. Moreover, there is also room for improvement on the other side: by setting up a more formal and balanced tradeoff between regular season performance and championship history, the macro-model can get up to 70+% without danger of significant over-fitting.

In fairness, I should note that the 5-by-5 model has had a bit of a rough patch recently—but, in its defense, so has every other model. The NBA has had some wacky results recently, but there is no indication that stats have supplanted history. Indeed, if you break the historical record into groups of more-predictable and less-predictable seasons, the 5-by-5 model trumps pure statistical models in all of them.

Uncertainty and Series Lengths

Finally, I’d like to quickly address the complete botching of series-length analysis that I put forward last year. Not only did I make a really elementary mistake in my explanation (that an emailer thankfully pointed out), but I’ve come to reject my ultimate conclusion as well.

Aside from strategic considerations, I’m now fairly certain that picking the home team in 5 or the away team in 6 is always right, no matter how close you think the series is. I first found this result when running playoff simulations that included margin for error (in other words, accounting for the fact that teams may be better or worse than their stats would indicate, or that they may match up more or less favorably than the underlying records would suggest), but I had some difficulty getting this result to comport with the empirical data, which still showed “home team in 6” as the most common outcome.  But now I think I’ve figured this problem out, and it has to do with the fact that a lot of those outcomes came in spots where you should have picked the other team, etc. But despite the extremely simple-sounding outcome,  it’s a rich and interesting topic, so I’ll save the bulk of it for another day.

Starting this Week: Crappier Posts! (but, you know, posts)

There’s no denying that it has been pretty slow around here this year.  This is partly due to my unreliable new co-blogger:

I mean, it’s practically like I have to teach him everything from scratch.

On the other hand, I think this has just exacerbated a pre-existing issue, which is my chronic terror that something I post might not be interesting or awesome or air-tight enough (Incidentally, this is one reason I don’t publish model results or predictions very often: Even if they’re right, they’re still going to be wrong half the time, which is obv unacceptable). This gets even worse after any period of inactivity, since I feel extra pressure to come back with a bang.  But expecting everything I post to be a 150-page ebook in the making is pretty ridiculous, especially now that my time is more of a limited resource.

After considering various options, I’ve decided the best thing to do is commit to a minimal but rigid release schedule, quality be damned. So, starting tomorrow, I will be posting something every Monday, Wednesday, and Friday by 5PM PST, even if I have to pull a thought out of thin air at 4:45 and text it in. Presumably this will decrease the average quality of my posts, but I’m hopeful that it will be an improvement on no posts at all (no guarantees).

Tomorrow’s edition will be some odds and ends about this year’s ESPN Stat Geek Smackdown. But after that, it’s mystery meat as far as the eye can see.