The Case Against the Case for Dennis Rodman: Initial Volleys

When I began writing about Dennis Rodman, I was so terrified that I would miss something and the whole argument would come crashing down that I kept pushing it further and further and further, until a piece I initially planned to be about 10 pages of material ended up being more like 150. [BTW, this whole post may be a bit too inside-baseball if you haven’t actually read—or at least skimmed—my original “Case for Dennis Rodman.” If so, that link has a helpful guide.]

The downside of this, I assumed, is that the extra material should open up many angles of attack. It was a conscious trade-off, knowing that individual parts in the argument would be more vulnerable, but the Case as a whole would be thorough and redundant enough to survive any battles I might end up losing.

Ultimately, however, I’ve been a bit disappointed in the critical response. Most reactions I’ve seen have been either extremely complimentary or extremely dismissive.

So a while ago, I decided that if no one really wanted to take on the task, I would do it myself. In one of the Rodman posts, I wrote:

Give me an academic who creates an interesting and meaningful model, and then immediately devotes their best efforts to tearing it apart!

And thus The Case Against the Case for Dennis Rodman is born.

Before starting, here are a few qualifying points:

  1. I’m not a lawyer, so I have no intention of arguing things I don’t believe. I’m calling this “The Case Against the Case For Dennis Rodman,” because I cannot in good faith (barring some new evidence or argument I am as yet unfamiliar with) write The Case Against Dennis Rodman.
  2. Similarly, where I think an argument is worth being raised and discussed but ultimately fails, I will make the defense immediately (much like “Objections and Replies”).
  3. I don’t have an over-arching anti-Case hypothesis to prove, so don’t expect this series to be a systematic takedown of the entire enterprise. Rather, I will point out weaknesses as I consider them, so they may not come in any kind of predictable order.
  4. If you were paying attention, of course you noticed that The Case For Dennis Rodman was really (or at least concurrently) about demonstrating how player valuation is much more dynamic and complicated than either conventional or unconventional wisdom gives it credit for. But, for now, The Case Against the Case will focus mainly on the Dennis Rodman part.

Ok, so with this mission in mind, let me start with a bit of what’s out there already:

A Not-Completely-Stupid Forum Discussion

I admit, I spend a fair amount of time following back links to my blog. Some of that is just ego-surfing, but I’m also desperate to find worthy counter-arguments.

As I said above, that search is sometimes more fruitless than I would like. Even the more intelligent discussions usually include a lot of uninspired drivel. For example, let’s look at a recent thread on RealGM. After one person lays out a decent (though imperfect) summary of my argument, there are several responses along the lines of poster “SVictor”s:

I won’t pay attention to any study that states that [Rodman might be more valuable than Michael Jordan].

Actually, I’m pretty sympathetic to this kind of objection. There can be a bayesian ring of truth to “that is just absurd on its face” arguments (I once made a similar argument against an advanced NFL stat after it claimed Neil O’Donnell was the best QB in football). However, it’s not really a counter-argument, it’s more a meta-argument, and I think I’ve considered most of those to death. Besides, I don’t actually make the claim in question, I merely suggest it as something worth considering.

A much more detailed and interesting response comes from poster “mysticbb.” Now, he starts out pretty insultingly:

The argumentation is biased, it is pretty obvious, which makes it really sad, because I know how much effort someone has to put into such analysis.

I cannot say affirmatively that I have no biases, or that bias never affects my work. Study after study shows that this is virtually impossible. But I can say that I am completely and fundamentally committed to identifying it and stamping it out wherever I can. So, please—as I asked in my conclusion—please point out where the bias is evident and I will do everything in my power to fix it.

Oddly, though, mysticbb seems to endorse (almost verbatim) the proposition that I set out to prove:

Let me start with saying that Dennis Rodman seems to be underrated by a lot of people. He was a great player and deserved to be in the HOF, I have no doubt about that. He had great impact on the game and really improved his team while playing.

(People get so easily distracted: You write one article about a role-player maybe being better than Michael Jordan, and they forget that your overall claim is more modest.)

Of course, my analysis could just be way off, particularly in ways that favor Rodman. To that end, mysticbb raises several valid points, though with various degrees of significance.

Here he is on Rodman’s rebounding:

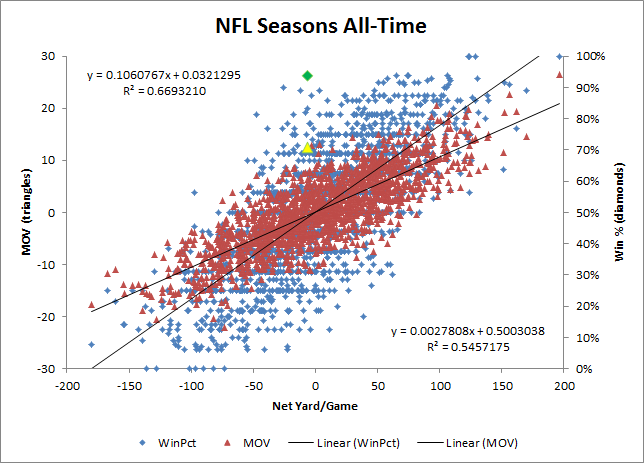
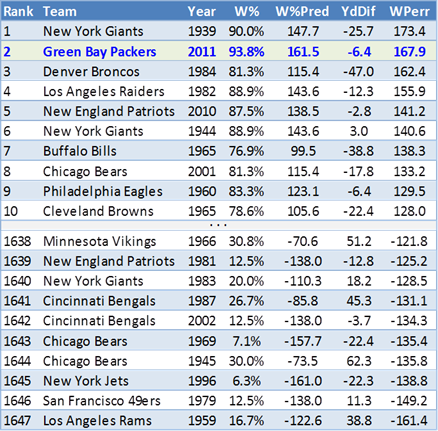
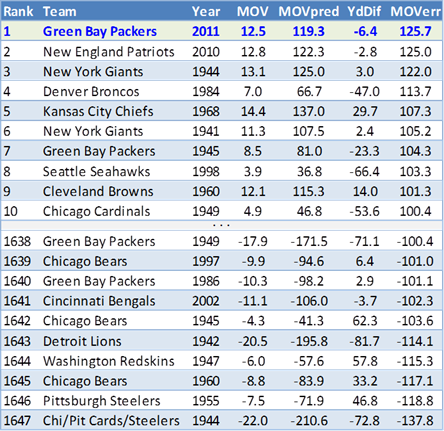
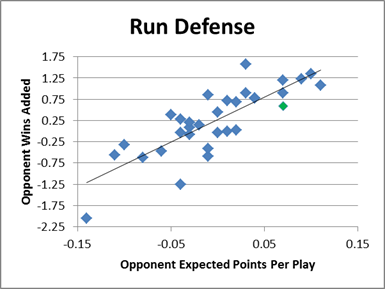
Let me start with the rebounding aspect. From 1991 to 1998 Rodman was leading the league in TRB% in each season. He had 17.7 ORB%, 33 DRB% and overall 25.4 TRB%. Those are AWESOME numbers, if we ignore context. Let us take a look at the numbers for the playoffs during the same timespan: 15.9 ORB%, 27.6 DRB% and 21.6 TRB%. Still great numbers, but obviously clearly worse than his regular season numbers. Why? Well, Rodman had the tendency to pad his rebounding stats in the regular season against weaker teams, while ignoring defensive assignments and fighting his teammates for rebounds. All that was eliminated during the playoffs and his numbers took a hit.

Now, I don’t know how much I talked about the playoffs per se, but I definitely discussed—and even argued myself—that Rodman’s rebounding numbers are likely inflated. But I also argued that if that IS the case, it probably means Rodman was even more valuable overall (see that same link for more detail). He continues:

Especially when we look at the defensive rebounding part, during the regular season he is clearly ahead of Duncan or Garnett, but in the playoffs they are all basically tied. Now imagine, Rodman brings his value via rebounding, what does that say about him, if that value is matched by players like Duncan or Garnett who both are also great defenders and obviously clearly better offensive players?

Now, as I noted at the outset Rodman’s career offensive rebounding percentage is approximately equal to Kevin Garnett’s career overall rebounding percentage, so I think Mystic is making a false equivalency based on a few cherry-picked stats.

But, for a moment, let’s assume it were true that Garnett/Duncan had similar rebounding numbers to Rodman, so what? Rodman’s crazy rebounding numbers cohere nicely with the rest of the puzzle as an explanation of why he was so valuable—his absurd rebounding stats make his absurd impact stats more plausible and vice versa—but they’re technically incidental. Indeed, they’re even incidental to his rebounding contribution: The number (or even percent) of rebounds a player gets does not correlate very strongly with the number of rebounds he has actually added to his team (nor does a player’s offensive “production” correlate very strongly with improvement in a team’s offense), and it does so the most on the extremes.

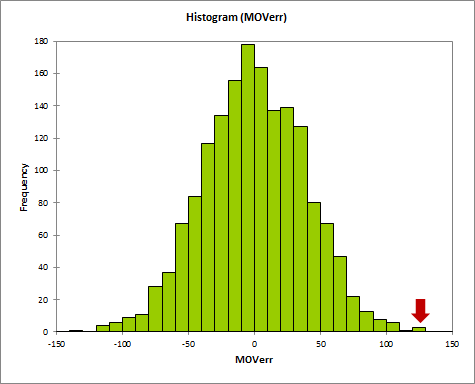
But I give the objection credit in this regard: The playoff/regular season disparity in Rodman’s rebounding numbers (though let’s not overstate the case, Rodman has 3 of the top 4 TRB%’s in playoff history) do serve to highlight how dynamic basketball statistics are. The original Case For Dennis Rodman is perhaps too willing to draw straight causal lines, and that may be worth looking into. Also, a more thorough examination of Rodman’s playoff performance may be in order as well.

On the indirect side of The Case, mysticbb has this to say:

[T]he high difference between the team performance in games with Rodman and without Rodman is also caused by a difference in terms of strength of schedule, HCA and other injured players.

I definitely agree that my crude calculation of Win % differentials does not control for a number of things that could be giving Rodman, or any other player, a boost. Controlling for some of these things is probably possible, if more difficult than you might think. This is certainly an area where I would like to implement some more robust comparison methods (and I’m slowly working on it).

But, ultimately, all of the factors mysticbb mentions are noise. Circumstances vary and lots of things happen when players miss games, and there are a lot of players and a lot of circumstances in the sample that Rodman is compared to: everyone has a chance to get lucky. That chance is reflected in my statistical significance calculations.

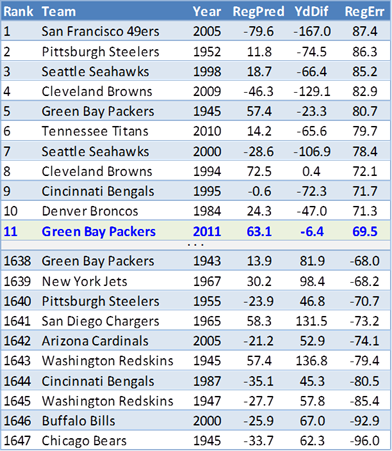
Mysticbb makes some assertions about Rodman having a particularly favorable schedule, but cites only the 1997 Bulls, and it’s pretty thin gruel:

If we look at the 12 games with Kukoc instead of Rodman we are getting 11.0 SRS. So, Rodman over Kukoc made about 0.5 points.

Of course, if there is evidence that Rodman was especially lucky over his career, I would like to see it. But, hmm, since I’m working on the Case Against myself, I guess that’s my responsibility as well. Fair enough, I’ll look into it.

Finally, mysticbb argues:

The last point which needs to be considered is the offcourt issues Rodman caused, which effected the outcome of games. Take the 1995 Spurs for example, when Rodman refused to guard Horry on the perimeter leading to multiple open 3pt shots for Horry including the later neck-breaker in game 6. The Spurs one year later without Rodman played as good as in 1995 with him.

I don’t really have much to say on the first part of this. As I noted at the outset, there’s some chance that Rodman caused problems on his team, but I feel completely incompetent to judge that sort of thing. But the other part is interesting: It’s true that the Spurs were only 5% worse in 95-96 than they were in 94-95 (OFC, they would be worse measuring only against games Rodman played in), but cross-season comparisons are obviously tricky, for a number of reasons. And if they did exist, I’m not sure they would break the way suggested. For example, the 2nd Bulls 3-peat teams were about as much better than the first Bulls 3-peat as the first Bulls 3-peat was better than the 93-95 teams that were sans Michael Jordan.

That said, I actually do find multi-season comparisons to be a valid area for exploration. So, e.g., I’ve spent some time looking at rookie impact and how predictive it is of future success (answer: probably more than you think).

Finally, a poster named “parapooper” makes some points that he credits to me, including:

He also admits that Rodman actually has a big advantage in this calculation because he missed probably more games than any other player due to reasons other than health and age.

I don’t actually remember making this point, at least this explicitly, but it is a valid concern IMO. A lot of the In/Out numbers my system generated include seasons where players were old or infirm, which disadvantages them. In fact, I initially tried to excise these seasons, and tried accounting for them in a variety of ways, such as comparing “best periods” to “best periods”, etc. But I found such attempts to be pretty unwieldy and arbitrary, and they shrunk the sample size more than I thought they were worth, without affecting the bottom line: Rodman just comes out on top of a smaller pile. That said, some advantage to Rodman relative to others must exist, and quantifying that advantage is a worthy goal.

A similar problem that “para” didn’t mention specifically is that a number of the in/out periods for players include spots where the player was traded. In subsequent analysis, I’ve confirmed what common sense would probably indicate: A player’s differential stats in trade scenarios are much less reliable. Future versions of the differential comparison should account for this, one way or another.

The differential analysis in the series does seem to be the area that most needs upgrading, though the constant trade-off between more information and higher quality information means it will never be as conclusive as we might want it to be. Not mentioned in this thread (that I saw), but what I will certainly deal with myself, are broader objections to the differential comparisons as an enterprise. So, you know. Stay tuned.

Championship Experience Matters! (Super Bowl Edition)

To complete “Championship Week” at Skeptical Sports, I thought I’d post a little fun research I did before this year’s Super Bowl.

Like basketball, teams with championship-winning experience outperform their regular-season records in the playoffs, especially if they make it to the Super Bowl.

So, a bit like my 5-by-5 model, I wanted to come up with a simple metric for picking the Super Bowl winner. Unlike its NBA cousin, however, this method only applies to the championship game, not to the entire playoffs. The main question is, how much better does a team with more Super Bowl winning experience do than it’s opponent?

I feel bad about my text/graphs ratio this week, so I thought I’d tell this story in pictures. Before testing the question, we need to pick the best time period. So, for what number of years does the metric “pick the team with the most super bowl wins” most often pick the ultimate winner:

This was a little surprising to me already: I thought for sure the best n would be a small number, but it turns out to be 6.

Counting 2012, there have been 26 Super Bowls where one team has won more championships in the previous 6 years than the other. Of those games, the team with the greater number has won 20, or 77% of the time—including the Giants. [True story: I was going to publish something on this research before this year’s Super Bowl, but, knowing that it predicted a New York win against the heavily favored Patriots, I chickened out.]

Of course, I’m sure most of you are just itching to pounce right now: Clearly the team with the most recent Super Bowl wins is usually going to be better, right? So clearly this must be confounding this result. So let’s compare it to the predictive accuracy of SRS (Simple Rating System, aka “Margin of Victory adjusted for Strength of Schedule”):

Looking at all 46 Super Bowls, the team with the higher SRS has won 26, or 57%. In Super Bowls where no team had more Super Bowl wins, SRS performs slightly better, correctly picking 12/20 (60%). But the real story is in the games where both had something to say: When SRS and L6 agreed, the team they both picked won 11/14 (79%). But when SRS and L6 disagreed—in other words, where one team had a higher SRS, but the other had more Super Bowl wins in the previous 6 years—the team with the paper qualifications lost to the team with the championship experience 9 of 12 times (75%).

Now, your next thought might be that the years when L6 trumped SRS were probably the years when the teams were very close. But you’d be wrong:

The average SRS difference in 9 years where the L6 team won is actually higher than in the 3 years when it lost!

So how much does L6 add overall? Well, let’s first create a simple method, a bit like 5-by-5:

  1. If one team has more Super Bowl wins in the previous 6 years, pick them.
  2. Otherwise, pick the team with the best SRS.

Following this method, you would correctly pick 32 of the 46 Super Bowls (70%), for a 10% improvement overall, despite step 1 only even applying in about half of the games (also, note that if you just picked randomly in the 20 Super Bowls where L6 doesn’t apply, you would still be expected to get 30 right overall).

Finally, to try to quantify the difference in predictive value between the two measures, I plugged them both into a logistic regression:

As you can see, L6 is much more predictive, though the 95% confidence intervals do overlap. (Though I should also note, this last chart is based on the regression I ran prior to this year’s game, which ended up being another victory for the championship experience side.)

Championship Experience Matters! (Un-Sexy Version)

So in Monday’s post, I included my “5-by-5” method (I probably shouldn’t call it a “model”) for picking NBA champions. In case you missed it, here it is again:

  1. If there are any teams within 5 games of the best record that have won a title within the past 5 years, pick the most recent winner.
  2. Otherwise, pick the team with the best record.

In the 28 seasons since the NBA moved to a 16-team playoff format, this method correctly picked the eventual champion 18 times (64%), comparing favorably to the 10/28 (36%) success rate of the team with the league’s best record.

Henry Abbott blogged about it on ESPN yesterday, raising the obvious follow-up:

The question is, why? Why are teams that have won before so much better at winning again? I’ll kick off the brainstorming:

  • Maybe most teams fall short of their potential because of team dynamics of selfishness — and maybe champions are the teams that know how to move past that.
  • Maybe there are only a few really special coaches, and these teams have them.
  • Maybe there are only a few really special teams, and these teams are them.
  • Maybe there are special strategies to the playoffs that only some teams know. Not even sure what I’m talking about here — Sleep schedules? Nutrition? Injury prevention?
  • Maybe champions get better treatment from referees.

Anyway, it’s certainly fascinating.

UPDATE: John Hollinger with a good point that fits this and other data: Maybe title-winning team don’t value the regular season much.

Though I think some of these ideas are more on point than others, I won’t try to go parse every possibility. On balance, I’m sympathetic to the idea that “winning in the playoffs” has its own skillset independent of just being good at winning basketball games. Conceptually, it’s not too big a leap from the well-documented idea that winning games has its own skillset independent of scoring and allowing points (though the evidence is a lot more indirect).

That said, I think the biggest factor behind this result may be a bit less sexy: It may simply be a matter of information reliability.

Winning Championships is Harder than Winning Games

In stark contrast to other team sports, the NBA Playoffs are extremely deterministic. The best team usually wins (and, conversely, the winner is usually the best team). I’ve made this analogy many times before, but I’ll make it again: The NBA playoffs are a lot more like a Major tournament in men’s tennis than any other crowning competition in popular sports.

This is pretty much a function of design: A moderately better team becomes a huge favorite in a 7 game series. So even if the best team is only moderately better than the 2nd best team, they can be in a dominant position.

Combine this with an uneven distribution of talent (which, incidentally, is probably a function of salary structure), and mix in the empirical reality that the best teams normally don’t change very much from year to year, and its unsurprising that “dynasties” are so common.

On the other side of the equation, regular season standings and leaderboards—whether of wins or its most stable proxies—are highly variable. Note that a 95% confidence interval on an 82 game sample (aka, the “margin of error”) is +/- roughly 10 games.

If you think of the NBA regular season as a lengthy 30-team competition for the #1 seed, its structure is much, much less favorable to the best teams than the playoffs: It’s more like a golf tournament than a tennis tournament.

The Rest is Bayes

Obviously better teams win more often and vice-versa. It’s just that these results have to be interpreted in a context where all results were not equally likely ex ante. For example, the teams who post top records who also have recent championships are far more likely than others to actually be as good as their records indicate. This is pure bayesian inference.

Quick tangent: In my writing, I often reach a point where I say something along the lines of: “From there, it’s all bayesian inference.” I recognize that, for a lot of readers, this is barely a step up from an Underpants Gnomes argument. When I go there, it’s pretty much shorthand for “this is where results inform our beliefs about how likely various causes are to be true” (and all that entails).

There was an interesting comment on Abbott’s ESPN post, pointing out that the 5-by-5 method only picked 5/14 (35.7%) of champions correctly between 1967 and 1980. While there may be unrelated empirical reasons for this, I think this stat may actually confirm the underlying concept. Structurally, having fewer teams in the playoffs, shorter series lengths, a smaller number of teams in the league—basically any of the structural differences between the two eras I can think of—all undermine the combined informational value of [having a championship + having a top record].

To be fair, there may be any number of things in a particular season that undermine our confidence in this inference (I can think of some issues with this season’s inputs, obv). That’s the tricky part of bayesian reasoning: It turns on how plausible you thought things were already.

Stat Geek Smackdown 2012, Round 1: Odds and Ends

So in case any of you haven’t been following, the 2012 edition of the ESPN True Hoop Stat Geek Smackdown  is underway.  Now, obviously this competition shouldn’t be taken too seriously, as it’s roughly the equivalent of picking a weekend’s worth of NFL games, and last year I won only after picking against my actual opinion in the Finals (with good reason, of course).  That said, it’s still a lot of fun to track, and basketball is a deterministic-enough sport that I do think skill is relevant. At least enough that I will talk shit if I win again.

To that end, the first round is going pretty well for me so far.  Like last year, the experts are mostly in agreement. While there is a fair amount of variation in the series length predictions, there are only two matchups that had any dissent as to the likely winner: the 6 actual stat geeks split 4-2 in favor of the Lakers over the Nuggets, and 3-3 between the Clippers and the Grizzlies.  As it happens, I have both Los Angeles teams (yes, I am from Homer), as does Matthew Stahlhut (though my having the Lakers in 5 instead of 7 gives me a slight edge for the moment).  No one has gained any points on anyone else yet, but here is my rough account of possible scenarios:

[table “9” not found /]

On to some odds and ends:

The Particular Challenges of Predicting 2012

Making picks this year was a bit harder than in years past.  At one point I seriously considered picking Dallas against OKC (in part for strategic purposes), before reason got the better of me.  Abbott only published part of my comment on the series, so here’s the full version I sent him:

Throughout NBA history, defending champions have massively over-performed in the playoffs relative to their regular season records, so I wouldn’t count Dallas out.  In fact, the spot Dallas finds itself in is quite similar to Houston’s in 1995, and this season’s short lead -time and compressed schedule should make us particularly wary of the usual battery of predictive models.

Thus, if I had to pick which of these teams is more likely to win the championship, I might take Dallas (or at least it would be a closer call).  But that’s a far different question from who is most likely to win this particular series: Oklahoma City is simply too solid and Dallas too shaky to justify an upset pick. E.g., my generic model makes OKC a >90% favorite, so even a 50:50 chance that Dallas really is the sleeping giant Mark Cuban dreams about probably wouldn’t put them over the top.

That last little bit is important: The “paper gap” between Dallas and OKC is so great that even if Dallas were considerably better than they appeared during the regular season, that would only make them competitive, while if they were about as good as they appeared, they would be a huge dog (this kind of situation should be very familiar to any serious poker players out there).

But why on earth would I think Dallas might be any good in the first place? Well, I’ll discuss more below why champions should never be ignored, but the “paper difference” this year should be particularly inscrutable.  The normal methods for predicting playoff performance (both my own and others) are particularly ill-suited for the peculiar circumstances of this season:

  1. Perhaps most obviously, fewer regular season games means smaller sample sizes.  In turn, this means that sample-sensitive indicators (like regular season statistics) should have less persuasive value relative to non-sensitive ones (like championship pedigree).  It also affects things like head to head record, which is probably more valuable than a lot of stats people think, though less valuable than a lot of non-stats people think.  I’ve been working on some research about this, but for an example, look at this post about how I thought there seemed to be a market error w/r/t Dallas vs. Miami in game 6, partly b/c of the bayesian value of Dallas’s head to head advantage.
  2. Injuries are a bigger factor. This is not just that there are more of them (which is debatable), but there is less flexibility to effectively manage them: e.g., there’s obv less time to rehab players, but also less time to develop new line-ups and workarounds or make other necessary adjustments. In other words, a very good team might be hurt more by a role-player being injured than usual.
  3. What is the most reliable data? Two things I discussed last year were that (contra unconventional wisdom) Win% is more reliable for post-season predictions than MOV-type stats, and that (contra conventional wisdom) early season performance is typically more predictive than late season performance.  But both of these are undermined by the short season.  The fundamental value of MOV is as a proxy for W% that is more accurate for smaller sample sizes. And the predictive power of early-season performance most likely stems from its being more representative of playoff basketball: e.g., players are more rested and everyone tries their hardest.  However, not only are these playoffs not your normal playoffs, but this season was thrown together so quickly that a lot of teams had barely figured out their lineups by the quarter-pole. While late-season records have the same problems as usual, they may be more predictive just from being more similar to years past.
  4. Finally, it’s not just the nature of the data, but the nature of the underlying game as well. For example, in a lockout year, teams concerned with injury may be quicker to pull starting players in less lopsided scenarios than usual, making MOV less useful, etc. I won’t go into every possible difference, but here’s a related Twitter exchange:


Which brings us to the next topic:

The Simplest Playoff Model You’ll Never Beat

The thing that Henry Abbott most highlighted from my Smackdown picks (which he quoted at least 3 times in 3 different places) was my little piece of dicta about the Spurs:

I have a ‘big pot’ playoff model (no matchups, no simulations, just stats and history for each playoff team as input) that produces some quirky results that have historically out-predicted my more conventional models. It currently puts San Antonio above 50 percent. Not just against Utah, but against the field. Not saying I believe it, but there you go.

I really didn’t mean for this to be taken so seriously: it’s just one model.  And no, I’m not going to post it. It’s experimental, and it’s old and needs updating (e.g., I haven’t adjusted it to account for last season yet).

But I can explain why it loves the Spurs so much: it weights championship pedigree very strongly, and the Spurs this year are the only team near the top that has any.

Now some stats-loving people argue that the “has won a championship” variable is unreliable, but I think they are precisely wrong.  Perhaps this will change going forward, but, historically, there are no two ways to cut it: No matter how awesomely designed and complicated your models/simulations are, if you don’t account for championship experience, you will lose to even the most rudimentary model that does.

So case in point, I came up with this 2-step method for picking NBA Champions:

  1. If there are any teams within 5 games of the best record that have won a title within the past 5 years, pick the most recent.
  2. Otherwise, pick the team with the best record.

Following this method, you would correctly pick the eventual NBA Champion in 64.3% of years since the league moved to a 16-team playoff in 1984 (with due respect to the slayer, I call this my “5-by-5” model ).

Of course, thinking back, it seems like picking the winner is sometimes easy, as the league often has an obvious “best team” that is extremely unlikely to ever lose a 7 game series.  So perhaps the better question to ask is: How much do you gain by including the championship test in step 1?

The answer is: a lot. Over the same period, the team with the league’s best record has won only 10/28 championships, or ~35%. So the 5-by-5 model almost doubles your hit rate.

And in case you’re wondering, using Margin of Victory, SRS, or any other advanced stat instead of W-L record doesn’t help: other methods vary from doing slightly worse to slightly better. While there may still be room to beef up the complexity of your predictive model (such as advanced stats, situational simulations, etc), your gains will be (comparatively) marginal at best. Moreover, there is also room for improvement on the other side: by setting up a more formal and balanced tradeoff between regular season performance and championship history, the macro-model can get up to 70+% without danger of significant over-fitting.

In fairness, I should note that the 5-by-5 model has had a bit of a rough patch recently—but, in its defense, so has every other model. The NBA has had some wacky results recently, but there is no indication that stats have supplanted history. Indeed, if you break the historical record into groups of more-predictable and less-predictable seasons, the 5-by-5 model trumps pure statistical models in all of them.

Uncertainty and Series Lengths

Finally, I’d like to quickly address the complete botching of series-length analysis that I put forward last year. Not only did I make a really elementary mistake in my explanation (that an emailer thankfully pointed out), but I’ve come to reject my ultimate conclusion as well.

Aside from strategic considerations, I’m now fairly certain that picking the home team in 5 or the away team in 6 is always right, no matter how close you think the series is. I first found this result when running playoff simulations that included margin for error (in other words, accounting for the fact that teams may be better or worse than their stats would indicate, or that they may match up more or less favorably than the underlying records would suggest), but I had some difficulty getting this result to comport with the empirical data, which still showed “home team in 6” as the most common outcome.  But now I think I’ve figured this problem out, and it has to do with the fact that a lot of those outcomes came in spots where you should have picked the other team, etc. But despite the extremely simple-sounding outcome,  it’s a rich and interesting topic, so I’ll save the bulk of it for another day.

Starting this Week: Crappier Posts! (but, you know, posts)

There’s no denying that it has been pretty slow around here this year.  This is partly due to my unreliable new co-blogger:

I mean, it’s practically like I have to teach him everything from scratch.

On the other hand, I think this has just exacerbated a pre-existing issue, which is my chronic terror that something I post might not be interesting or awesome or air-tight enough (Incidentally, this is one reason I don’t publish model results or predictions very often: Even if they’re right, they’re still going to be wrong half the time, which is obv unacceptable). This gets even worse after any period of inactivity, since I feel extra pressure to come back with a bang.  But expecting everything I post to be a 150-page ebook in the making is pretty ridiculous, especially now that my time is more of a limited resource.

After considering various options, I’ve decided the best thing to do is commit to a minimal but rigid release schedule, quality be damned. So, starting tomorrow, I will be posting something every Monday, Wednesday, and Friday by 5PM PST, even if I have to pull a thought out of thin air at 4:45 and text it in. Presumably this will decrease the average quality of my posts, but I’m hopeful that it will be an improvement on no posts at all (no guarantees).

Tomorrow’s edition will be some odds and ends about this year’s ESPN Stat Geek Smackdown. But after that, it’s mystery meat as far as the eye can see.

Sports Geek Mecca: Recap and Thoughts, Part 1

So, over the weekend, I attended my second MIT Sloan Sports Analytics Conference. My experience was much different than in 2011: Last year, I went into this thing barely knowing that other people were into the same things I was. An anecdote: In late 2010, I was telling my dad how I was about to have a 6th or 7th round interview for a pretty sweet job in sports analysis, when he speculated, “How many people can there even be in that business? 10? 20?” A couple of months later, of course, I would learn.

A lot has happened in my life since then: I finished my Rodman series, won the ESPN Stat Geek Smackdown (which, though I am obviously happy to have won, is not really that big a deal—all told, the scope of the competition is about the same as picking a week’s worth of NFL games), my wife and I had a baby, and, oh yeah, I learned a ton about the breadth, depth, and nature of the sports analytics community.

For the most part, I used Twitter as sort of my de facto notebook for the conference.  Thus, I’m sorry if I’m missing a bunch of lengthier quotes and/or if I repeat a bunch of things you already saw in my live coverage, but I will try to explain a few things in a bit more detail.

For the most part, I’ll keep the recap chronological.  I’ve split this into two parts: Part 1 covers Friday, up to but not including the Bill Simmons/Bill James interview.  Part 2 covers that interview and all of Saturday.

Opening Remarks:

From the pregame tweets, John Hollinger observed that 28 NBA teams sent representatives (that we know of) this year.  I also noticed that the New England Revolution sent 2 people, while the New England Patriots sent none, so I’m not sure that number of official representatives reliably indicates much.

The conference started with some bland opening remarks by Dean David Schmittlein.  Tangent: I feel like political-speak (thank everybody and say nothing) seems to get more and more widespread every year. I blame it on fear of the internet. E.g., in this intro segment, somebody made yet another boring joke about how there were no women present (personally, I thought there were significantly more than last year), and was followed shortly thereafter by a female speaker, understandably creating a tiny bit of awkwardness. If that person had been more important (like, if I could remember his name to slam him), I doubt he would have made that joke, or any other joke. He would have just thanked everyone and said nothing.

The Evolution of Sports Leagues

Featuring Gary Bettman (NHL), Rob Manfred (MLB), Adam Silver (NBA), Steve Tisch (NYG) and Michael Wilbon moderating.

This panel really didn’t have much of a theme, it was mostly Wilbon creatively folding a bunch of predictable questions into arbitrary league issues.  E.g.: ” “What do you think about Jeremy Lin?!? And, you know, overseas expansion blah blah.”

I don’t get the massive cultural significance of Jeremy Lin, personally.  I mean, he’s not the first ethnically Chinese player to have NBA success (though he is perhaps the first short one).  The discussion of China, however, was interesting for other reasons. Adam Silver claimed that Basketball is already more popular in China than soccer, with over 300 million Chinese people playing it.  Those numbers, if true, are pretty mind-boggling.

Finally, there was a whole part about labor negotiations that was pretty well summed up by this tweet:

Hockey Analytics

Featuring Brian Burke, Peter Chiarelli, Mike Milbury and others.

The panel started with Peter Chiarelli being asked how the world champion Boston Bruins use analytics, and in an ominous sign, he rambled on for a while about how, when it comes to scouting, they’ve learned that weight is probably more important than height.

Overall, it was a bit like any scene from the Moneyball war room, with Michael Schuckers (the only pro-stats guy) playing the part of Jonah Hill, but without Brad Pitt to protect him.

When I think of Brian Burke, I usually think of Advanced NFL Stats, but apparently there’s one in Hockey as well.  Burke is GM/President of the Toronto Maple Leafs. At one point he was railing about how teams that use analytics have never won anything, which confused me since I haven’t seen Toronto hoisting any Stanley Cups recently, but apparently he did win a championship with the Mighty Ducks in 2007, so he clearly speaks with absolute authority.

This guy was a walking talking quote machine for the old school. I didn’t take note of all the hilarious and/or non-sensical things he said, but for some examples, try searching Twitter for “#SSAC Brian Burke.” To give an extent of how extreme, someone tweeted this quote at me, and I have no idea if he actually said it or if this guy was kidding.

In other words, Burke was literally too over the top to effectively parody.

On the other hand, in the discussion of concussions, I thought Burke had sort of a folksy realism that seemed pretty accurate to me.  I think his general point is right, if a bit insensitive: If we really changed hockey so much as to eliminate concussions entirely, it would be a whole different sport (which he also claimed no one would watch, an assertion which is more debatable imo).  At the end of the day, I think professional sports mess people up, including in the head.  But, of course, we can’t ignore the problem, so we have to keep proceeding toward some nebulous goal.

Mike Milbury, presently a card-carrying member of the media, seemed to mostly embrace the alarmist media narrative, though he did raise at least one decent point about how the increase in concussions—which most people are attributing to an increase in diagnoses—may relate to recent rules changes that have sped up the game.

But for all that, the part that frustrated me the most was when Michael Schuckers, the legitimate hockey statistician at the table, was finally given the opportunity to talk.  90% of the things that came out of his mouth were various snarky ways of asserting that face-offs don’t matter.  I mean, I assume he’s 100% right, but just had no clue how to talk to these guys.  Find common ground: you both care about scoring goals, defending goals, and winning.  Good face-off skill get you the puck more often in the right situations. The question is how many extra possessions you get and how valuable those possessions are? And finally, what’s the actual decision in question?

Baseball Analytics

Featuring Scott Boras, Scott Boras, Scott Boras, some other guys, Scott Boras, and, oh yeah, Bill James.

In stark constrast to the Hockey panel, the Baseball guys pretty much bent over backwards to embrace analytics as much as possible.  As I tweeted at the time:

Scott Boras seems to like hearing Scott Boras talk.  Which is not so bad, because Scott Boras actually did seem pretty smart and well informed: Among other things, Scott Boras apparently has a secret internal analytics team. To what end, I’m not entirely sure, since Scott Boras also seemed to say that most GM’s overvalue players relative to what Scott Boras’s people tell Scott Boras.

At this point, my mind wandered:

How awesome would that be, right?

Anyway, in between Scott Boras’s insights, someone asked this Bill James guy about his vision for the future of baseball analytics, and he gave two answers:

  1. Evaluating players from a variety of contexts other than the minor leagues (like college ball, overseas, Cubans, etc).
  2. Analytics will expand to look at the needs of the entire enterprise, not just individual players or teams.

Meh, I’m a bit underwhelmed.  He talked a bit about #1 in his one-on-one with Bill Simmons, so I’ll look at that a bit more in my review of that discussion. As for #2, I think he’s just way way off: The business side of sports is already doing tons of sophisticated analytics—almost certainly way more than the competition side—because, you know, it’s business.

E.g., in the first panel, there was a fair amount of discussion of how the NBA used “sophisticated modeling” for many different lockout-related analyses (I didn’t catch the Ticketing Analytics panel, but from its reputation, and from related discussions on other panels, it sounds like that discipline has some of the nerdiest analysis of all).

Scott Boras let Bill James talk about a few other things as well:  E.g., James is not a fan of new draft regulations, analogizing them to government regulations that “any economist would agree” inevitably lead to market distortions and bursting bubbles.  While I can’t say I entirely disagree, I’m going to go out on a limb and guess that his political leanings are probably a bit Libertarian?

Basketball Analytics

Featuring Jeff Van Gundy, Mike Zarren, John Hollinger, and Mark Cuban Dean Oliver.

If every one of these panels was Mark Cuban + foil, it would be just about the most awesome weekend ever (though you might not learn the most about analytics). So I was excited about this one, which, unfortunately, Cuban missed. Filling in on zero/short notice was Dean Oliver.  Overall, here’s Nathan Walker’s take:

This panel actually had some pretty interesting discussions, but they flew by pretty fast and often followed predictable patterns, something like this:

  1. Hollinger says something pro-stats, though likely way out of his depth.
  2. Zarren brags about how they’re already doing that and more on the Celtics.
  3. Oliver says something smart and nuanced that attempts to get at the underlying issues and difficulties.
  4. Jeff Van Gundy uses forceful pronouncements and “common sense” to dismiss his strawman version of what the others have been saying.

E.g.:

Zarren talked about how there is practically more data these days than they know what to do with.  This seems true and I think it has interesting implications. I’ll discuss it a little more in Part 2 re: the “Rebooting the Box Score” talk.

There was also an interesting discussion of trades, and whether they’re more a result of information asymmetry (in other words, teams trying to fleece each other), or more a result of efficient trade opportunities (in other words, teams trying to help each other).  Though it really shouldn’t matter—you trade when you think it will help you, whether it helps your trade partner is mostly irrelevant—Oliver endorsed the latter.  He makes the point that, with such a broad universe of trade possibilities, looking for mutually beneficial situations is the easiest way to find actionable deals.  Fair enough.

Coaching Analytics

Featuring coaching superstars Jeff Van Gundy, Eric Mangini, and Bill Simmons.  Moderated by Daryl Morey.

OK, can I make the obvious point that Simmons and Morey apparently accidentally switched role cards?  As a result, this talk featured a lot of Simmons attacking coaches and Van Gundy defending them.  I honestly didn’t remember Mangini was on this panel until looking back at the book (which is saying something, b/c Mangini usually makes my blood boil).

There was almost nothing on, say, how to evaluate coaches, say, by analyzing how well their various decisions comported with the tenets of win maximization.  There was a lengthy (and almost entirely non-analytical) discussion of that all-important question of whether an NBA coach should foul or not up by 3 with little time left.  Fouling probably has a tiny edge, but I think it’s too close and too infrequent to be very interesting (though obviously not as rare, it reminds me a bit of the impassioned debates you used to see on Poker forums about whether you should fast-play or slow-play flopped quads in limit hold’em).

There was what I thought was a funny moment when Bill Simmons was complaining about how teams seem to recycle mediocre older coaches rather than try out young, fresh talent. But when challenged by Van Gundy, Simmons drew a blank and couldn’t think of anyone.  So, Bill, this is for you.  Here’s a table of NBA coaches who have coached at least 1000 games for at least 3 different teams, while winning fewer than 60% of their games and without winning any championships:

[table “8” not found /]

Note that I’m not necessarily agreeing with Simmons: Winning championships in the NBA is hard, especially if your team lacks uber-stars (you know, Michael Jordan, Magic Johnson, Dennis Rodman, et al).

Part 2 coming soon!

Honestly, I got a little carried away with my detailed analysis/screed on Bill James, and I may have to do a little revising. So due to some other pressing writing commitments, you can probably expect Part 2 to come out this Saturday (Friday at the earliest).

Graph of the Day: Quarterbacks v. Coaches, Draft Edition

[Note: With the recent amazing addition to my office, I’ve considered just turning this site into a full-on baby photo-blog (much like my Twitter feed).  While that would probably mean a more steady stream of content, it would also probably require a new name, a re-design, and massive structural changes.  Which, in turn, would raise a whole bevy of ontological issues that I’m too tired to deal with at the moment. So I guess back to sports analysis!]

In “A History of Hall of Fame QB-Coach Entanglement,” I talked a bit about the difficulty of “detangling” QB and coach accomplishments.  For a slightly more amusing historical take, here’s a graph illustrating how first round draft picks have gotten a much better return on investment (a full order of magnitude better vs. non-#1 overalls) when traded for head coaches than when used to draft quarterbacks:

Note: Since 1950. List of #1 Overall QB’s is here.  Other 1st Round QB’s here.  Other drafted QB’s here.  Super Bowl starters here.  QB’s that were immediately traded count for the team that got them.

Note*: . . that I know of. I googled around looking for coaches that cost their teams at least one first round draft pick to acquire, and I could only find 3: Bill Parcells (Patriots -> Jets), Bill Belichick (Jets -> Patriots), and Jon Gruden (Raiders -> Bucs).  If I’m missing anyone, please let me know.

Sample, schmample.

But seriously, the other 3 bars are interesting too.

Thoughts on the Packers Yardage Anomaly

In their win over Detroit on Sunday, Green Bay once again managed to emerge victorious despite giving up more yards than they gained. This is practically old hat for them, as it’s the 10th time that they’ve done it this year. Over the course of the season, the 15-1 Packers gave up a stunning 6585 yards, while gaining “just” 6482—thus losing the yardage battle despite being the league’s most dominant team.

This anomaly certainly captures the imagination, and I’ve received multiple requests for comment.  E.g., a friend from my old poker game emails:

Just heard that the Packers have given up more yards than they’ve gained and was wondering how to explain this.  Obviously the Packers’ defense is going to be underrated by Yards Per Game metrics since they get big leads and score quickly yada yada, but I don’t see how this has anything to do with the fact they’re being outgained.  I assume they get better starting field position by a significant amount relative to their opponents so they can have more scoring drives than their opponents while still giving up more yards than they gain, but is that backed up by the stats?

Last week Advanced NFL Stats posted a link to this article from Smart Football looking into the issue in a bit more depth. That author does a good job examining what this stat means, and whether or not it implies that Green Bay isn’t as good as they seem (he more or less concludes that it doesn’t).

But that doesn’t really answer the question of how the anomaly is even possible, much less how or why it came to be.  With that in mind, I set out to solve the problem.  Unfortunately, after having looked at the issue from a number of angles, and having let it marinate in my head for a week, I simply haven’t found an answer that I find satisfying.  But, what the hell, one of my resolutions is to pull the trigger on this sort of thing, so I figure I should post what I’ve got.

How Anomalous?

The first thing to do when you come across something that seems “crazy on its face” is to investigate how crazy it actually is (frequently the best explanation for something unusual is that it needs no explanation).  In this case, however, I think the Packers’ yardage anomaly is, indeed, “pretty crazy.”  Not otherworldly crazy, but, say, on a scale of 1 to “Kurt Warner being the 2000 MVP,” it’s at least a 6.

First, I was surprised to discover that just last year, the New England Patriots also had the league’s best record (14-2), and also managed to lose the yardage battle.  But despite such a recent example of a similar anomaly, it is still statistically pretty extreme.  Here’s a plot of more or less every NFL team season from 1936 through the present, excluding seasons where the relevant stats weren’t available or were too incomplete to be useful (N=1647):

The green diamond is the Packers net yardage vs. Win%, and the yellow triangle is their net yardage vs. Margin of Victory (net points).  While not exactly Rodman-esque outliers, these do turn out to be very historically unusual:

Win %

Using the trendline equation on the graph above (plus basic algebra), we can use a team’s season Win percentage to calculate their expected yardage differential.  With that prediction in hand, we can compare how much each team over or under-performed its “expectation”:

Both the 2011 Packers and the 2010 Patriots are in the top 5 all-time, and I should note that the 1939 New York Giants disparity is slightly overstated, because I excluded tie games entirely (ties cause problems elsewhere b/c of perfect correlation with MOV).

Margin of Victory

Toward the conclusion of that Smart Football article, the author notes that Green Bay’s Margin of Victory isn’t as strong as their overall record, noting that the Packers “Pythagorian Record” (expectation computed from points scored and points allowed) is more like 11-5 or 12-4 than 15-1 (note that getting from extremely high Win % to very high MOV is incidental: 15-win teams are usually 11 or 12 win teams that have experienced good fortune).  Green Bay’s MOV of 12.5 is a bit lower than the historical average for 15-1 teams (13.8) but don’t let this mislead you: the disparity between the yardage differential that we would expect based on Green Bay’s MOV and their actual result (using a linear projection, as above) is every bit as extreme as what we saw from Win %:

And here, in histogram form:

So, while not the most unusual thing to ever happen in sports, this anomaly is certainly unusual enough to look into.

For the record, the Packers’ MOV -> yard diff error is 3.23 standard deviations above the mean, while the Win% -> yard diff is 3.28.  But since MOV correlates more strongly with the target stat (note an average error of only 125 yards instead of 170), a similar degree of abnormality leaves it as the more stable and useful metric to look at.

Thus, the problem can be framed as follows: The 2011 Packers fell around 2000 yards (the 125.7 above * 16 games) short of their expected yardage differential.  Where did that 2000 yard gap come from?

Possible Factors and/or Explanations

Before getting started, I should note that, out of necessity, some of these “explanations” are more descriptive than actually explanatory, and even the ones that seem plausible and significant are hopelessly mixed up with one another.  At the end of the day, I think the question of “What happened?” is addressable, though still somewhat unclear.  The question of “Why did it happen?” remains largely a mystery: The most substantial claim that I’m willing to make with any confidence is that none of the obvious possibilities are sufficient explanations by themselves.

While I’m somewhat disappointed with this outcome, it makes sense in a kind of Fermi Paradox, “Why Aren’t They Here Yet?” kind of way.  I.e., if any of the straightforward explanations (e.g., that their stats were skewed by turnovers or “garbage time” distortions) could actually create an anomaly of this magnitude, we’d expect it to have happened more often.

And indeed, the data is actually consistent with a number of different factors (granted, with significant overlap) being present at once.

Line of Scrimmage, and Friends

As suggested in the email above, one theoretical explanation for the anomaly could be the Packers’ presumably superior field position advantage.  I.e., with their offense facing comparatively shorter fields than their opponents, they could have literally had fewer yards available to gain.  This is an interesting idea, but it turns out to be kind of a bust.

The Packers did enjoy a reciprocal field position advantage of about 5 yards.  But, unfortunately, there doesn’t seem to be a noticeable relationship between average starting field position and average yards gained per drive (which would have to be true ex ante for this “explanation” to have any meaning):

Note: Data is from the Football Outsiders drive stats.

This graph plots both offenses and defenses from 2011.  I didn’t look at more historical data, but it’s not really necessary: Even if a larger dataset revealed a statistically significant relationship, the large error rate (which converges quickly) means that it couldn’t alter expectation in an individual case by more than a fraction of a yard or so per possession.  Since Green Bay only traded 175ish possessions this season, it couldn’t even make a dent in our 2000 missing yards (again, that’s if it existed at all).

On the other hand, one thing in the F.O. drive stats that almost certainly IS a factor, is that the Packers had a net of 10 fewer possessions this season than their opponents.  As Green Bay averaged 39.5 yards per possession, this difference alone could account for around 400 yards, or about 20% of what we’re looking for.

Moreover, 5 of those 10 possessions come from a disparity in “zero yard touchdowns,” or net touchdowns scored by their defense and special teams: The Packers scored 7 of these (5 from turnovers, 2 from returns) while only allowing 2 (one fumble recovery and one punt return).  Such scores widen a team’s MOV without affecting their total yardage gap.

[Warning: this next point is a bit abstract, so feel free to skip to the end.] Logically, however, this doesn’t quite get us where we want to go.  The relevant question is “What would the yardage differential have been if the Packers had the same number of possessions as their opponents?”  Some percentage of our 10 counterfactual drives would result in touchdowns regardless.  Now, the Packers scored touchdowns on 37% of their actual drives, but scored touchdowns on at least 50% of their counterfactual drives (the ones that we can actually account for via the “zero yard touchdown” differential).  Since touchdown drives are, on average, longer than non-touchdown drives, this means that the ~400 yards that can be attributed to the possession gap is at least somewhat understated.

Garbage Time

When considering this issue, probably the first thing that springs to minds is that the Packers have won a lot of games easily.  It seems highly plausible that, having rushed out to so many big leads, the Packers must have played a huge amount of “garbage time,” in which their defense could have given up a lot of “meaningless” yards that had no real consequence other than to confound statisticians.

The proportion of yards on each side of the ball that came after Packers games got out of hand should be empirically checkable—but, unfortunately, I haven’t added 2011 Play-by-Play data to my database yet.  That’s okay, though, because there are other ways—perhaps even more interesting ways—to attack the problem.

In fact, it’s pretty much right up my alley: Essentially, what we are looking for here is yet another permutation of “Reverse Clutch” (first discussed in my Rodman series, elaborated in “Tim Tebow and the Taxonomy of Clutch”). Playing soft in garbage time is a great way for a team to “underperform” in statistical proxies for true strength.  In football, there are even a number of sound tactical and strategic reasons why you should explicitly sacrifice yards in order to maximize your chances of winning.  For example, if you have a late lead, you should be more willing to soften up your defense of non-sideline runs and short passes—even if it means giving up more yards on average than a conventional defense would—since those types of plays hasten the end of the game.  And the converse is true on offense:  With a late lead, you want to run plays that avoid turnovers and keep the clock moving, even if it means you’ll be more predictable and easier to defend.

So how might we expect this scenario to play out statistically?  Recall, by definition, “clutch” and “reverse clutch” look the same in a stat sheet.  So what kind of stats—or relationships between stats—normally indicate “clutchness”?  As it turns out, Brian Burke at Advanced NFL Stats has two metrics pretty much at the core of everything he does: Expected Points Added, and Win Percentage Added.  The first of these (EPA) takes the down and distance before and after each play and uses historical empirical data to model how much that result normally affects a team’s point differential.  WPA adds time and score to the equation, and attempts to model the impact each play has on the team’s chances of winning.

A team with “clutch” results—whether by design or by chance—might be expected to perform better in WPA (which ultimately just adds up to their number of wins) than in EPA (which basically measures generic efficiency).

For most aspects of the game, the relationship between these two is strong enough to make such comparisons possible.  Here are plots of this comparison for each of the 4 major categories (2011 NFL, Green Bay in green), starting with passing offense (note that the comparison is technically between wins added overall and expected points per play):

And here’s passing defense:

Rushing offense:

And rushing defense:

Obviously there’s nothing strikingly abnormal about Green Bay’s results in these graphs, but there are small deviations that are perfectly consistent with the garbage time/reverse clutch theory.  For the passing game (offense and defense), Green Bay seems to hew pretty close to expectation.  But in the rushing game they do have small but noticeable disparities on both sides of the ball.  Note that in the scenario I described where a team intentionally trades efficiency for win potential, we would expect the difference to be most acute in the running game (which would be under-defended on defense and overused on offense).

Specifically: Green Bay’s offensive running game has a WPA of 1.1, despite having an EPA per play of zero (which corresponds to a WPA of .25).  On defense, the Packers’ EPA/p is .07, which should correspond to an expected WPA of 1.0, while their actual result is .59.

Clearly, both of these effects are small, considering there isn’t a perfect correlation.  But before dismissing them entirely, I should note that we don’t immediately know how much of the variation in the graphs above is due to variance for a given team and how much is due to variation between teams.  Moreover, without knowing the balance, the fact that both variance and variation contribute to the “entropy” of the observed relationship between EPA/p and WPA, the actual relationship between the two is likely to be stronger than these graphs would make it seem.

The other potential problem is that this comparison is between wins and points, while the broader question is comparing points to yards.  But there’s one other statistical angle that helps bridge the two, while supporting the speculated scenario to boot: Green Bay gained 3.9 yards per attempt on offense, and allowed 4.7 yards per attempt on defense—while the league average is 4.3 yards per attempt.  So, at least in terms of raw yardage, Green Bay performed “below average” in the running game by about .4 yards/attempt on each side of the ball.  Yet, the combined WPA for the Packers running game is positive! Their net rushing WPA is +.5, despite having an expected combined WPA (actually based on their EPA) of -.75.

So, if we thought this wasn’t a statistical artifact, there would be two obvious possible explanations: 1) That Green Bay has a sub-par running game that has happened to be very effective in important spots, or 2) that Green Bay actually has an average (or better) running game that has appeared ineffective (especially as measured by yards gained/allowed) in less important spots. Q.E.D.

For the sake of this analysis, let’s assume that the observed difference for Green Bay here really is a product of strategic adjustments stemming from (or at least related to) their winning ways, how much of our 2000 yard disparity could it account for?

So let’s try a crazy, wildly speculative, back-of-the-envelope calculation: Give Green Bay and its opponents the same number of rushing attempts that they had this season, but with both sides gaining an average number of yards per attempt.  The Packers had 395 attempts and their opponents had 383, so at .4 yards each, the yardage differential would swing by 311 yards.  So again, interesting and plausibly significant, but doesn’t even come close to explaining our anomaly on its own.

Turnover Effect?

One of the more notable features of the Packers season is their incredible +22 turnover margin.  How they managed that and whether it was simply variance or something more meaningful could be its own issue.  But in this context, give them the +22, how helpful is that as an explanation for the yardage disparity?  Turnovers affect scores and outcomes a ton, but are relatively neutral w/r/t yards, so surely this margin is relevant.  But exactly how much does it neutralize the problem?

Here, again, we can look at the historical data.  To predict yardage differential based on MOV and turnover differential, we can set up an extremely basic linear regression:

The R-Square value of .725 means that this model is pretty accurate (MOV alone achieved around .66).  Both variables are extremely significant (from p value, or absolute value of t-stat).  Based on these coefficients, the resulting predictive equation is

YardsDiff = 7.84*MOV – 23.3*TOdiff/gm

Running the dataset through the same process as above (comparing predictions with actual results and calculating the total error), here’s how the new rankings turns out:

In other words, if we account for turnovers in our predictions, the expected/actual yardage discrepancy drops from ~125 to ~70 yards per game.  This obv makes the results somewhat less extreme, though still pretty significant: 11th of 1647.  Or, in histogram form:

So what’s the bottom line?  At 69.5 yards per game, the total “missing” yardage drops to around 1100.  Therefore, inasmuch as we accept it as an “explanation,” Green Bay’s turnover differential seems to account for about 900 yards.

It’s probably obvious, but important enough to say anyway, that there is extensive overlap between this “explanation” and our others above: E.g., the interception differential contributes to the possession differential, and is exacerbated by garbage time strategy, which causes the EPA/WPA differential, etc.

“Bend But Don’t Break”

Finally, I have to address a potential cause of this anomaly that I would almost rather not: The elusive “Bend But Don’t Break” defense.  It’s a bit like the Dark Matter of this scenario: I can prove it exists, and estimate about how much is there, but that doesn’t mean I have any idea what it is or where it comes from, and it’s almost certainly not as sexy as people think it is.

Typically, “Bend But Don’t Break” is the description that NFL analysts use for bad defenses that get lucky.  As a logical and empirical matter, they mostly don’t make sense: Pretty much every team in history (save, possibly, the 2007 New England Patriots) has a steeply inclined expected points by field position curve.  See, e.g., the “Drive Results” chart in this post.  Any time you “bend” enough to give up first downs, you’re giving up expected points. In other words, barring special circumstances, there is simply no way to trade significant yards for a decreased chance of scoring.

Of course, you can have defenses that are stronger at defending various parts of the field, or certain down/distance combinations, which could have the net effect of allowing fewer points than you would expect based on yards allowed, but that’s not some magical defensive rope-a-dope strategy, it’s just being better at some things than others.

But for whatever reason, on a drive-by-drive basis, did the Green Bay defense “bend” more than it “broke”? In other words, did they give up fewer points than expected?

And the answer is “yes.”  Which should be unsurprising, since it’s basically a minor variant of the original problem.  In other words, it begs the question.

In fact, with everything that we’ve looked at so far, this is pretty much all that is left: if there weren’t a significant “Bend But Don’t Break” effect observable, the yardage anomaly would be literally impossible.

And, in fact, this observation “accounts” for about 650 yards, which, combined with everything else we’ve looked at (and assuming a modest amount of overlap), puts us in the ballpark of our initial 2000 yard discrepancy.

Extremely Speculative Conclusions

Some of the things that seem speculative above must be true, because there has to be an accounting: even if it’s completely random, dumb luck with no special properties and no elements of design, there still has to be an avenue for the anomaly to manifest.

So, given that some speculation is necessary, the best I can do is offer a sort of “death by a thousand cuts” explanation.  If we take the yardage explained by turnovers, the “dark matter” yards of “bend but don’t break”, and then roughly half of our speculated consequences of the fewer drives/zero yard TD’s and the “Garbage Time” reverse-clutch effect (to account for overlap), you actually end up with around 2100 yards, with a breakdown like so:

So why cut drives and reverse clutch in half instead of the others?  Mostly just to be conservative. We have to account for overlap somewhere, and I’d rather leave more in the unknown than in the known.

At the end of the day, the stars definitely had to align for this anomaly to happen: Any one of the contributing factors may have been slightly unusual, but combine them and you get something rare.

Google Autocomplete Error in My Favor

So I was scanning for funny search terms that have led wary surfers to the blog, but stumbled into the following instead (click to enlarge):

In case you’re wondering, yes, I signed out of Google and turned off search personalization first.  The URL of the search just leads to “the case for dennis rodman” results, so if you want to duplicate it, you have to enter “+/- for Dennis Rodman” yourself (without pressing enter or the search button, obv).  Incidentally, this site is only the #6 result for the original search.

I understand that my humble offering may be the only study of Dennis Rodman’s +/- stats in existence (I have no idea), but, regardless, this seems like a clear flaw in the autocomplete algorithm to me. Personally, I would like to see Google get better at making semantic distinctions, while this seems to flub one of the most basic: between search term and search result.

Incidentally, I was just going to title this post “Dennis Rodman Still Looks Like the Scariest Clown Ever,” but I didn’t want to set expectations too high.