Quantum Randy Moss—An Introduction to Entanglement

[Update: This post from 2010 has been getting some renewed attention in response to Randy Moss’s mildly notorious statement in New Orleans. I’ve posted a follow-up with more recent data here: “Is Randy Moss the Greatest?” For discussion of the broader idea, however, you’re in the right place.]

As we all know, even the best-intentioned single-player statistical metrics will always be imperfect indicators of a player’s skill. They will always be impacted by external factors such as variance, strength of opponents, team dynamics, and coaching decisions. For example, a player’s shooting % in basketball is a function of many variables – such as where he takes his shots, when he takes his shots, how often he is double-teamed, whether the team has perimeter shooters or big space-occupying centers, how often his team plays Oklahoma, etc – only one of which is that player’s actual shooting ability. Some external factors will tend to even out in the long-run (like opponent strength in baseball). Others persist if left unaccounted for, but are relatively easy to model (such as the extra value of made 3 pointers, which has long been incorporated into “true shooting percentage”). Some can be extremely difficult to work with, but should at least be possible to model in theory (such as adjusting a running back’s yards per carry based on the run-blocking skill of their offensive line). But some factors can be impossible (or at least practically impossible) to isolate, thus creating systematic bias that cannot be accurately measured. One of these near-impossible external factors is what I call “entanglement,” a phenomenon that occurs when more than one player’s statistics determine and depend on each other. Thus, when it comes to evaluating one of the players involved, you run into an information black hole when it comes to the entangled statistic, because it can be literally impossible to determine which player was responsible for the relevant outcomes.

While this problem exists to varying degrees in all team sports, it is most pernicious in football. As a result, I am extremely skeptical of all statistical player evaluations for that sport, from the most basic to the most advanced. For a prime example, no matter how detailed or comprehensive your model is, you will not be able to detangle a quarterback’s statistics from those of his other offensive skill position players, particularly his wide receivers. You may be able to measure the degree of entanglement, for example by examining how much various statistics vary when players change teams. You may even be able to make reasonable inferences about how likely it is that one player or another should get more credit, for example by comparing the careers of Joe Montana with Kansas City and Jerry Rice with Steve Young (and later Oakland), and using that information to guess who was more responsible for their success together. But even the best statistics-based guess in that kind of scenario is ultimately only going to give you a probability (rather than an answer), and will be based on a miniscule sample.

Of course, though stats may never be the ultimate arbiter we might want them to be, they can still tell us a lot in particular situations. For example, if only one element (e.g., a new player) in a system changes, corresponding with a significant change in results, it may be highly likely that that player deserves the credit (note: this may be true whether or not it is reflected directly in his stats). The same may be true if a player changes teams or situations repeatedly with similar outcomes each time. With that in mind, let’s turn to one of the great entanglement case-studies in NFL history: Randy Moss.
I’ve often quipped to my friends or other sports enthusiasts that I can prove that Randy Moss is probably the best receiver of all time in 13 words or less. The proof goes like this:

Chad Pennington, Randall Cunningham, Jeff George, Daunte Culpepper, Tom Brady, and Matt Cassell.

The entanglement between QB and WR is so strong that I don’t think I am overstating the case at all by saying that, while a receiver needs a good quarterback to throw to him, ultimately his skill-level may have more impact on his quarterback’s statistics than on his own. This is especially true when coaches or defenses key on him, which may open up the field substantially despite having a negative impact on his stat-line. Conversely, a beneficial implication of such high entanglement is that a quarterback’s numbers may actually provide more insight into a wide receiver’s abilities than the receiver’s own – especially if you have had many quarterbacks throwing to the same receiver with comparable success, as Randy Moss has.

Before crunching the data, I would like to throw some bullet points out there:

There have been 6 quarterbacks who have started 9 or more games in a season with Randy Moss as one of their receivers (for obvious reasons, I have replaced Chad Pennington with Kerry Collins for this analysis).
Only two of them had starting jobs in the seasons immediately prior to those with Moss (Kerry Collins, Tom Brady).
Only one of them had a starting job in the season immediately following those with Moss (Matt Cassell).
Pro Bowl appearances of quarterbacks throwing to Moss: 6. Pro-Bowl appearances of quarterbacks after throwing to Moss: 0.
Daunte Culpepper made the Pro Bowl 3 times in his 5 seasons throwing to Moss. He has won a combined 5 games as a starting quarterback in 5 seasons since.

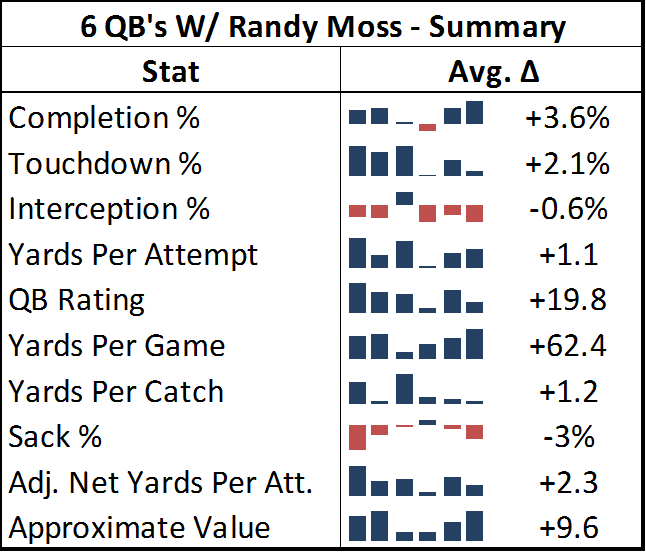
With the exception of Kerry Collins, all of the QB’s who have thrown to Moss have had “career” years with him (Collins improved, but not by as much at the others). To illustrate this point, I’ve compiled a number of popular statistics for each quarterback for their Moss years and their other years, in order to figure out the average affect Moss has had. To qualify as a “Moss year,” they had to have been his quarterback for at least 9 games. I have excluded all seasons where the quarterback was primarily a reserve, or was only the starting quarterback for a few games. The “other” seasons include all of that QB’s data in seasons without Moss on his team. This is not meant to bias the statistics, the reason I exclude partial seasons in one case and not the other is that I don’t believe occasional sub work or participation in a QB controversy accurately reflects the benefit of throwing to Moss, but those things reflect the cost of not having Moss just fine. In any case, to be as fair as possible, I’ve included the two Daunte Culpepper seasons where he was seemingly hampered by injury, and the Kerry Collins season where Oakland seemed to be in turmoil, all three of which could arguably not be very representative.

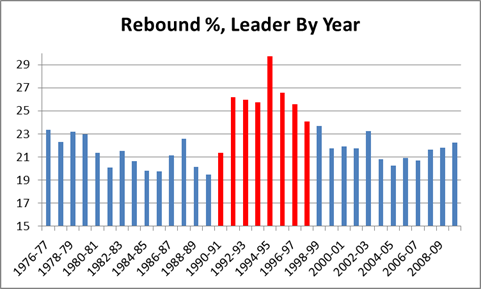
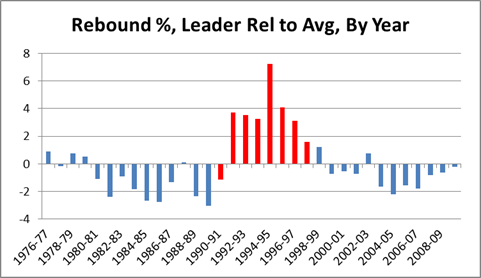
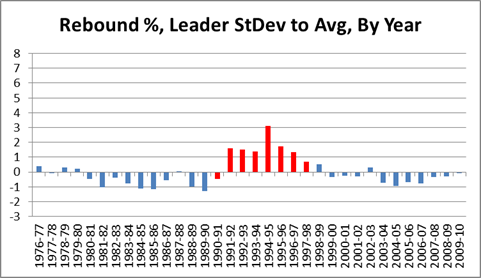
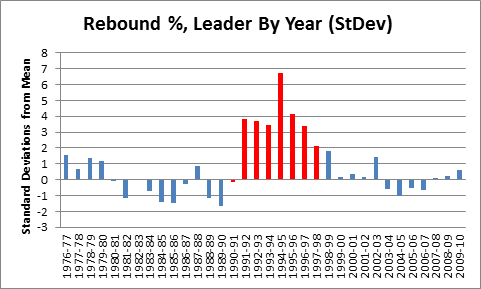
As you can see in the table below, the quarterbacks throwing to Moss posted significantly better numbers across the board:

_{[Edit to note: in this table’s sparklines and in the charts below, the 2nd and third positions are actually transposed from their chronological order. Jeff George was Moss’s 2nd quarterback and Culpepper was his 3rd, rather than vice versa. This happened because I initially sorted the seasons by year and team, forgetting that George and Culpepper both came to Minnesota at the same time.]}

^{Note: Adjusted Net Yards Per Attempt incorporates yardage lost due to sacks, plus gives bonuses for TD’s and penalties for interceptions. Approximate Value is an advanced stat from Pro Football Reference that attempts to summarize all seasons for comparison across positions. Details here.}

Out of 60 metrics, only 3 times did one of these quarterbacks fail to post better numbers throwing to Moss than in the rest of his career: Kerry Collins had a slightly lower completion percentage and slightly higher sack percentage, and Jeff George had a slightly higher interception percentage for his 10-game campaign in 1999 (though this was still his highest-rated season of his career). For many of these stats, the difference is practically mind-boggling: QB Rating may be an imperfect statistic overall, but it is a fairly accurate composite of the passing statistics that the broader football audience cares the most about, and 19.8 points is about the difference in career rating between Peyton Manning and J.P. Losman.

Though obviously Randy Moss is a great player, I still maintain that we can never truly measure exactly how much of this success was a direct result of Moss’s contribution and how much was a result of other factors. But I think it is very important to remember that, as far as highly entangled statistics like this go, independent variables are rare, and this is just about the most robust data you’ll ever get. Thus, while I can’t say for certain that Randy Moss is the greatest receiver in NFL History, I think it is unquestionably true that there is more statistical evidence of Randy Moss’s greatness than there is for any other receiver.

Full graphs for all 10 stats after the jump:

Read the rest of this entry »

Graph of the Day 2: NFL Regression—Descent Into Chaos

I guess it’s funky graph day here at SSA:
This one corresponds to the bubble-graphs in this post about regression to the mean before and after the introduction of the salary cap. Each colored ball represents one of the 32 teams, with wins in year n on the x axis and wins in year n+1 on the y axis. In case you don’t find the visual interesting enough in its own right, you’re supposed to notice that it gets crazier right around 1993.

Graph of the Day: Rodman, Visualized—An Outlier in Motion

(Just press play.)

The Case for Dennis Rodman, Part 1/4 (c)—Rodman v. Ancient History

One of the great false myths in basketball lore is that Wilt Chamberlain and Bill Russell were Rebounding Gods who will never be equaled, and that dominant rebounders like Dennis Rodman should count their blessings that they got to play in a era without those two deities on the court. This myth is so pervasive that it is almost universally referenced as a devastating caveat whenever sports commentators and columnists discuss Rodman’s rebounding prowess. In this section, I will attempt to put that caveat to death forever.

The less informed version of the “Chamberlain/Russell Caveat” (CRC for short) typically goes something like this: “Rodman led the league in rebounding 7 times, making him the greatest re bounder of his era, even though his numbers come nowhere near those of Chamberlain and Russell.” It is true that, barring some dramatic change in the way the game is played, Chamberlain’s record of 27.2 rebounds per game, set in the 1960-61 season, will stand forever. This is because, due to the fast pace and terrible shooting, the typical game in 1960-61 featured an average of 147 rebounding opportunities. During Rodman’s 7-year reign as NBA rebounding champion (from 1991-92 through 1997-98), the typical game featured just 84 rebounding opportunities. Without further inquiry, this difference alone means that Chamberlain’s record 27.2 rpg would roughly translate to 15.4 in Rodman’s era – over a full rebound less than Rodman’s ~16.7 rpg average over that span.

The slightly more informed (though equally wrong) version of the CRC is a plea of ignorance, like so: “Rodman has the top 7 rebounding percentages since the NBA started to keep the necessary statistics in 1970. Unfortunately, there is no game-by-game or individual opponent data prior to this, so it is impossible to tell whether Rodman was as good as Russell or Chamberlain” (this point also comes in many degrees of snarky, like, “I’ll bet Bill and Wilt would have something to say about that!!!”). We may not have the necessary data to calculate Russell and Chamberlain’s rebounding rates, either directly or indirectly. But, as I will demonstrate, there are quite simple and extremely accurate ways to estimate these figures within very tight ranges (which happen to come nowhere close to Dennis Rodman).

Before getting into rebounding percentages, however, let’s start with another way of comparing overall rebounding performance: Team Rebound Shares. Simply put, this metric is the percentage of team rebounds that were gotten by the player in question. This can be done for whole seasons, or it can be approximated over smaller periods, such as per-game or per-minute, even if you don’t have game-by-game data. For example, to roughly calculate the stat on a per-game basis, you can simply take a player’s total share of rebounds (their total rebounds/team’s total rebounds), and divide by the percentage of games they played (player gms/team gms). I’ve done this for all of Rodman, Russell and Chamberlain’s seasons, and organized the results as follows:

As we can see, Rodman does reasonably well in this metric, still holding the top 4 seasons and having a better average through 7. This itself is impressive, considering Rodman averaged about 35 minutes per game and Wilt frequently averaged close to 48.

I should note, in Chamberlain’s favor, that one of the problems I have with PER and its relatives is that they don’t give enough credit for being able to contribute extra minutes, as Wilt obviously could. However, since here I’m interested more in each player’s rebounding ability than in their overall value, I will use the same equation as above (plus dividing by 5, corresponding to the maximum minutes for each player) to break the team rebounding shares down by minute:

This is obviously where Rodman separates himself from the field, even pulling in >50% of his team’s rebounds in 3 different seasons. Of course, this only tells us what it tells us, and we’re looking for something else: Total Rebounding percentage. Thus, the question naturally arises: how predictive of TRB% are “minute-based team rebound shares”?

In order to answer this question, I created a slightly larger data-set, by compiling relevant full-season statistics from the careers of Dennis Rodman, Dwight Howard, Tim Duncan, David Robinson, and Hakeem Olajuwon (60 seasons overall). I picked these names to represent top-level rebounders in a variety of different situations (and though these are somewhat arbitrary, this analysis doesn’t require a large sample). I then calculated TRS by minute for each season and divided by 2 — roughly corresponding to the player’s share against 10 players instead of 5. Thus, all combined, my predictive variable is determined as follows:

$PV=\frac{Player Rebounds/Team Rebounds}{Player Minutes/Team Minutes}/10$

Note that this formula may have flaws as an independent metric, but if it’s predictive enough of the metric we really care about — Total Rebound % — those no longer matter. To that end, I ran a linear regression in Excel comparing this new variable to the actual values for TRB%, with the following output:

If you don’t know how to read this, don’t sweat it. The “R Square” of .98 pretty much means that our variable is almost perfectly predictive of TRB%. The two numbers under “Coefficients” tell us the formula we should use to make predictions based on our variable:

$Predicted TRB\% = 1.08983*PV - .01154$

Putting the two equations together, we have a model that predicts a player’s rebound percentage based on 4 inputs:

$TRB\% = 1.08983 * \frac{Player Rebounds/Team Rebounds}{Player Minutes/Team Minutes} /10 - .0115$

Now again, if you’re familiar with regression output, you can probably already see that this model is extremely accurate. But to demonstrate that fact, I’ve created two graphs that compare the predicted values with actual values, first for Dennis Rodman alone:

And then for the full sample:

So, the model seems solid. The next step is obviously to calculate the predicted total rebound percentages for each of Wilt Chamberlain and Bill Russell’s seasons. After this, I selected the top 7 seasons for each of the three players and put them on one graph (Chamberlain and Russell’s estimates vs. Rodman’s actuals):

It’s not even close. It’s so not close, in fact, that our model could be way off and it still wouldn’t be close. For the next two graphs, I’ve added error bars to the estimation lines that are equal to the single worst prediction from our entire sample (which was a 1.21% error, or 6.4% of the underlying number): [I should add a technical note, that the actual expected error should be slightly higher when applied to “outside” situations, since the coefficients for this model were “extracted” from the same data that I tested the model on. Fortunately, that degree of precision is not necessary for our purposes here.] First Rodman vs. Chamberlain:

Then Rodman vs. Russell:

In other words, if the model were as inaccurate in Russell and Chamberlain’s favor as it was for the worst data point in our data set, they would still be crushed. In fact, over these top 7 seasons, Rodman beats R&C by an average of 7.2%, so if the model understated their actual TRB% every season by 5 times as much as the largest single-season understatement in our sample, Rodman would still be ahead [edit: I’ve just noticed that Pro Basketball Reference has a TRB% listed for each of Chamberlain’s last 3 seasons. FWIW, this model under-predicts one by about 1%, over-predicts one by about 1%, and gets the third almost on the money (off by .1%)].

To stick one last dagger in CRC’s heart, I should note that this model predicts that Chamberlain’s best TRB% season would have been around 20.16%, which would rank 67th on the all-time list. Russell’s best of 20.08 would rank 72nd. Arbitrarily giving them 2% for the benefit of the doubt, their best seasons would still rank 22nd and 24th respectively.

This Week in Skeptical Sports Analysis

I’ve just returned from a weekend wedding getaway in NoCal, and I’m excited to get back to work on the blog. In this weekly feature (which will normally be posted on Sundays), I will post blog-related news, review some of the site activity from the previous week, give quick previews of what’s to come in the following week and what’s in the works, plus respond to any questions or requests.

Blog news:

There is now a sweet iPhone/mobile version of the blog, thanks to the WPTouch plug-in. To see it, just open the blog in any iPhone, Android, Blackberry or Palm Pre device.
I’ve added my Twitter feed to the right sidebar, using the Twitter Goodies plug-in. It works nicely, although it currently won’t display my re-tweets. If you happen to know how to fix this, please email me.
I added a “praise for Skeptical Sports” section to the “about this blog” page. By default, I assume that public statements of praise (e.g., from Twitter, in the comments, or on a public forum) are OK to duplicate there, but if for whatever reason you don’t want your statement to appear anymore, just let me know and I’ll remove it.
There’s a thread on 2+2 (a poker/gambling forum with an excellent sports section) about this blog that contains a decent amount of discussion about some of the topics I’ve posted on, especially Dennis Rodman and Carmello Anthony. It also includes some silly speculation about what my “secret identity” on 2+2 might be, but the sports analysis is interesting. Also, if any of those guys are reading, feel free to post in the comments here as well (and I don’t mind cross-posting).

Last week on the blog:

On Sunday, I posted an analysis of Tiger Woods’ horrible performance this year, focusing on whether it is consistent with a natural decline, and questioning what the consequences would be if the change is permanent.
On Monday I posted this criticism of Nate Silver criticizing an ESPN study about baseball umpiring.
On Tuesday and Friday I posted parts 1(a) and 1(b) of my Dennis Rodman series, both addressing the issue of just how good a rebounder he was.
On Wednesday I posted an article ostensibly about the 1-15 St. Louis Rams, which was really an attempt to quantify the effects of the salary cap on regression to the mean in the NFL.
On Thursday I conducted some “research” into the origins of the Brett Favre/Hamlet analogy, with entertaining results.

This week on the blog:

I will be posting parts 1(c) and 2 of my Rodman series. The first will examine whether Wilt Chamberlain and Bill Russell were the Gods of Rebounding that Bill Simmons and others always claim they were, and the second will try to pin down exactly how valuable Rodman’s rebounding was to the teams he played for (criticizing PER’s in the process).
I will be posting my Tennis Service Aggression Calculator, which will use a tiny bit of calculus to model whether a player should be more aggressive in their service game.
I will post something on the NFL, either a model for evaluating pre-season predictions that I’ve been working on, or my long-promised “Show Me a Quarterback that Doesn’t Throw Interceptions and I’ll Show You a Sucky Quarterback” analysis.

In the works:

Death, Taxes, and Randy Moss: a discussion of statistical entanglement in the NFL, and the implications for player analysis.
A comprehensive criticism of Hollinger statistics: This will probably be my next big series after the one on Rodman. I hate to do basketball back-to-back, but this research is practically done and dying to be published.
Is Usain Bolt a natural 400 runner?: An examination of the 10m splits for Bolt’s record-setting runs, and what they say about his top speed advantage and his endurance.

By request:

In the comments for Rodman 1(b), Jake asked what the “Ambicourtedness” graph would look like if Rodman were taken out of the sample. This was not difficult, particularly since it looks virtually the same. Here it is:

A friend privately asked me what other NBA stars’ Offensive v. Defensive rebound % graphs looked like, suggesting that, while there may be a tradeoff overall, that doesn’t necessarily mean that the particular lack of tradeoff that Rodman shows is rare. This is a very good question, so I looked at similar graphs for virtually every player who had 5 or more seasons in the “Ambicourtedness Top 1000.” There are other players who have positively sloping trend-lines, though none that come close to Rodman’s. I put together a quick graph to compare Rodman to a number of other big name players who were either great rebounders (e.g., Moses Malone), perceived-great rebounders (e.g., Karl Malone, Dwight Howard), or Charles Barkley:

If you have requests or questions that you would like me to answer on the blog, let me know. And it doesn’t have to be a follow-up to a post I’ve already made: If you have some completely different topic that you would like to see analyzed, or some article that you would like to see reviewed, let me know and I will try to get to it. I can promise that if I get any topic requests that meet the minimal interestingness threshold (that is, I think “hmm, interesting”), I will address at least one of them every week or so.

The Case for Dennis Rodman, Part 1/4 (b)—Defying the Laws of Nature

In this post I will be continuing my analysis of just how dominant Dennis Rodman’s rebounding was. Subsequently, section (c) will cover my analysis of Wilt Chamberlain and Bill Russell, and Part 2 of the series will begin the process of evaluating Rodman’s worth overall.

For today’s analysis, I will be examining a particularly remarkable aspect of Rodman’s rebounding: his ability to dominate the boards on both ends of the court. I believe this at least partially gets at a common anti-Rodman argument: that his rebounding statistics should be discounted because he concentrated on rebounding to the exclusion of all else. This position was publicly articulated by Charles Barkley back when they were both still playing, with Charles claiming that he could also get 18+ rebounds every night if he wanted to. Now that may be true, and it’s possible that Rodman would have been an even better player if he had been more well-rounded, but one thing I am fairly certain of is that Barkley could not have gotten as many rebounds as Rodman the same way that Rodman did.

The key point here is that, normally, you can be a great offensive rebounder, or you can be a great defensive rebounder, but it’s very hard to be both. Unless you’re Dennis Rodman:

To prepare the data for this graph, I took the top 1000 rebounding seasons by total rebounding percentage (the gold-standard of rebounding statistics, as discussed in section (a)), and ranked them 1-1000 for both offensive (ORB%) and defensive (DRB%) rates. I then scored each season by the higher (larger number) ranking of the two. E.g., if a particular season scored a 25, that would mean that it ranks in the top 25 all-time for offensive rebounding percentage and in the top 25 all-time for defensive rebounding percentage (I should note that many players who didn’t make the top 1000 seasons overall would still make the top 1000 for one of the two components, so to be specific, these are the top 1000 ORB% and DRB% seasons of the top 1000 TRB% seasons).

This score doesn’t necessarily tell us who the best rebounder was, or even who was the most balanced, but it should tell us who was the strongest in the weakest half of their game (just as you might rank the off-hand of boxers or arm wrestlers). Fortunately, however, Rodman doesn’t leave much room for doubt: his 1994-1995 season is #1 all-time on both sides. He has 5 seasons that are dual top-15, while no other NBA player has even a single season that ranks dual top-30. The graph thus shows how far down you have to go to find any player with n number of seasons at or below that ranking: Rodman has 6 seasons register on the (jokingly titled) “Ambicourtedness” scale before any other player has 1, and 8 seasons before any player has 2 (for the record, Charles Barkley’s best rating is 215).

This outcome is fairly impressive alone, and it tells us that Rodman was amazingly good at both ORB and DRB – and that this is rare — but it doesn’t tell us anything about the relationship between the two. For example, if Rodman just got twice as many rebounds as any normal player, we would expect him to lead lists like this regardless of how he did it. Thus, if you believe the hypothesis that Rodman could have dramatically increased his rebounding performance just by focusing intently on rebounds, this result might not be unexpected to you.

The problem, though, is that there are both competitive and physical limitations to how much someone can really excel at both simultaneously. Not the least of which is that offensive and defensive rebounds literally take place on opposite sides of the floor, and not everyone gets up and set for every possession. Thus, if someone wanted to cheat toward getting more rebounds on the offensive end, it would likely come, at least in some small part, at the expense of rebounds on the defensive end. Similarly, if someone’s playing style favors one, it probably (at least slightly), disfavors the other. Whether or not that particular factor is in play, at the very least you should expect a fairly strong regression to the mean: thus, if a player is excellent at one or the other, you should expect them to be not as good at the other, just as a result of the two not being perfectly correlated. To examine this empirically, I’ve put all 1000 top TRB% seasons on a scatterplot comparing offensive and defensive rebound rates:

Clearly there is a small negative correlation, as evidenced by the negative coefficient in the regression line. Note that technically, this shouldn’t be a linear relationship overall – if we graphed every pair in history from 0,0 to D,R, my graph’s trendline would be parallel to the tangent of that curve as it approaches Dennis Rodman. But what’s even more stunning is the following:

Rodman is in fact not only an outlier, he is such a ridiculously absurd alien-invader outlier that when you take him out of the equation, the equation changes drastically: The negative slope of the regression line nearly doubles in Rodman’s absence. In case you’ve forgotten, let me remind you that Rodman only accounts for 12 data points in this 1000 point sample: If that doesn’t make your jaw drop, I don’t know what will! For whatever reason, Rodman seems to be supernaturally impervious to the trade-off between offensive and defensive rebounding. Indeed, if we look at the same graph with only Rodman’s data points, we see that, for him, there is actually an extremely steep, upward sloping relationship between the two variables:

In layman’s terms, what this means is that Rodman comes in varieties of Good, Better, and Best — which is how we would expect this type of chart to look if there were no trade-off at all. Yet clearly the chart above proves that such a tradeoff exists! Dennis Rodman almost literally defies the laws of nature (or at least the laws of probability).

The ultimate point contra Barkley, et al, is that if Rodman “cheated” toward getting more rebounds all the time, we might expect that his chart would be higher than everyone else’s, but we wouldn’t have any particular reason to expect it to slope in the opposite direction. Now, this is slightly more plausible if he was “cheating” on the offensive side on the floor while maintaining a more balanced game on the defensive side, and there are any number of other logical speculations to be made about how he did it. But to some extent this transcends the normal “shift in degree” v. “shift in kind” paradigm: what we have here is a major shift in degree of a shift in kind, and we don’t have to understand it perfectly to know that it is otherworldly. At the very least, I feel confident in saying that if Charles Barkley or anyone else really believes they could replicate Rodman’s results simply by changing their playing styles, they are extremely naive.

Addendum (4/20/11):

Commenter AudacityOfHoops asks:

I don’t know if this is covered in later post (working my way through the series – excellent so far), or whether you’ll even find the comment since it’s 8 months late, but … did you create that same last chart, but for other players? Intuitively, it seems like individual players could each come in Good/Better/Best models, with positive slopes, but that when combined together the whole data set could have a negative slope.

I actually addressed this in an update post (not in the Rodman series) a while back:

A friend privately asked me what other NBA stars’ Offensive v. Defensive rebound % graphs looked like, suggesting that, while there may be a tradeoff overall, that doesn’t necessarily mean that the particular lack of tradeoff that Rodman shows is rare. This is a very good question, so I looked at similar graphs for virtually every player who had 5 or more seasons in the “Ambicourtedness Top 1000.” There are other players who have positively sloping trend-lines, though none that come close to Rodman’s. I put together a quick graph to compare Rodman to a number of other big name players who were either great rebounders (e.g., Moses Malone), perceived-great rebounders (e.g., Karl Malone, Dwight Howard), or Charles Barkley:

By my accounting, Moses Malone is almost certainly the 2nd-best rebounder of all time, and he does show a healthy dose of “ambicourtedness.” Yet note that the slope of his trendline is .717, meaning the difference between him and Rodman’s 2.346 is almost exactly twice the difference between him and the -.102 league average (1.629 v .819).

Hey, Do You Think Brett Favre is Maybe Like Hamlet?

On a lighter note: Earlier I was thinking about how tired I am of hearing various ESPN commentators complain about Brett Favre’s “Hamlet impression” – though I was just using the term “Hamlet impression” for the rant in my head, no one was actually saying it (at least this time). I quickly realized how completely unoriginal my internal dialogue was being, and after scolding myself for a few moments, I resolved to find the identity of the first person to ever make the Favre/Hamlet comparison.

Lo and behold, the earliest such reference in the history of the internet – that is, according to Google – was none other than Gregg Easterbrook, in this TMQ column from August 27th, 2003:

TMQ loves Brett Favre. This guy could wake up from a knee operation and fire a touchdown pass before yanking out the IV line. It’s going to be a sad day when he cuts the tape off his ankles for the final time. And it’s wonderful that Favre has played his entire (meaningful) career in the same place, honoring sports lore and appeasing the football gods, never demanding a trade to a more glamorous media market.

But even as someone who loves Favre, TMQ thinks his Hamlet act on retirement has worn thin. Favre keeps planting, and then denying, rumors that he is about to hang it up. He calls sportswriters saying he might quit, causing them to write stories about how everyone wants him to stay; then he calls more sportswriters denying that he will quit, causing them to write stories repeating how everyone wants him to stay. Maybe Favre needs to join a publicity-addiction recovery group. The retire/unretire stuff got pretty old with Frank Sinatra and Michael Jordan; it’s getting old with Favre.

Ha!

The 1-15 Rams and the Salary Cap—Watch Me Crush My Own Hypothesis

It is a quirky little fact that 1-15 teams have tended to bounce back fairly well. Since expanding to 16 games in 1978, 9 teams have hit the ignoble mark, including last year’s St. Louis Rams. Of the 8 that did it prior to 2009, all but the 1980 Saints made it back to the playoffs within 5 years, and 4 of the 8 eventually went on to win Super Bowls, combining for 8 total. The median number of wins for a 1-15 team in their next season is 7:

My grand hypothesis about this was that the implementation of the salary cap after the 1993-94 season, combined with some of the advantages I discuss below (especially 2 and 3), has been a driving force behind this small-but-sexy phenomenon: note that at least for these 8 data points, there seems to be an upward trend for wins and downward trend for years until next playoff appearance. Obviously, this sample is way too tiny to generate any conclusions, but before looking at harder data, I’d like to speculate a bit about various factors that could be at play. In addition to normally-expected regression to the mean, the chain of consequences resulting from being horrendously bad is somewhat favorable:

The primary advantages are explicitly structural: Your team picks at the top of each round in the NFL draft. According to ESPN’s “standard” draft-pick value chart, the #1 spot in the draft is worth over twice as much as the 16th pick [side note: I don’t actually buy this chart for a second. It massively overvalue 1st round picks and undervalues 2nd round picks, particularly when it comes to value added (see a good discussion here)]:
The other primary benefit, at least for one year, comes from the way the NFL sets team schedules: 14 games are played in-division and against common divisional opponents, but the last two games are set between teams that finished in equal positions the previous year (this has obviously changed many times, but there have always been similar advantages). Thus, a bottom-feeder should get a slightly easier schedule, as evidenced by the Rams having the 2nd-easiest schedule for this coming season.
There are also reliable secondary benefits to being terrible, some of which get greater the worse you are. A huge one is that, because NFL statistics are incredibly entangled (i.e., practically every player on the team has an effect on every other player’s statistics), having a bad team tends to drag everyone’s numbers down. Since the sports market – and the NFL’s in particular – is stats-based on practically every level, this means you can pay your players less than what they’re worth going forward. Under the salary cap, this leaves you more room to sign and retain key players, or go for quick fixes in free agency (which is generally unwise, but may boost your performance for a season or two).
A major tertiary effect – one that especially applies to 1-15 teams, is that embarrassed clubs tend to “clean house,” meaning, they fire coaches, get rid of old and over-priced veterans, make tough decisions about star players that they might not normally be able to make, etc. Typically they “go young,” which is advantageous not just for long-term team-building purposes, but because young players are typically the best value in the short term as well.
An undervalued quaternary effect is that new personnel and new coaching staff, in addition to hopefully being better at their jobs than their predecessors, also make your team harder to prepare for, just by virtue of being new (much like the “backup quarterback effect,” but for your whole team).
A super-important quinary effect is that. . . Ok, sorry, I can’t do it.

Of course, most of these effects are relevant to more than just 1-15 teams, so perhaps it would be better to expand the inquiry a tiny bit. For this purpose, I’ve compiled the records of every team since the merger, so beginning in 1970, and compared them to their record the following season (though it only affects one data point, I’ve treated the first Ravens season as a Browns season, and treated the new Browns as an expansion team). I counted ties as .5 wins, and normalized each season to 16 games (and rounded). I then grouped the data by wins in the initial season and plotted it on a “3D Bubble Chart.” This is basically a scatter-plot where the size of each data-point is determined by the number of examples (e.g., only 2 teams have gone undefeated, so the top-right bubble is very small). The 3D is not just for looks: the size of each sphere is determined by using the weights for volume, which makes it much less “blobby” than 2D, and it allows you to see the overlapping data points instead of just one big ink-blot:

^{*Note: again, the x-axis on this graph is wins in year n, and the y axis is wins in year n+1. Also, note that while there are only 16 “bubbles,” they represent well over a thousand data points, so this is a fairly healthy sample.}

The first thing I can see is that there’s a reasonably big and fat outlier there for 1-15 teams (the 2nd bubble from the left)! But that’s hardly a surprise considering we started this inquiry knowing that group had been doing well, and there are other issues at play: First, we can see that the graph is strikingly linear. The equation at the bottom means that to predict a team’s wins for one year, you should multiply their previous season’s win total by ~.43 and add ~4.7 (e.g.’s: an 8-win team should average about 8 wins the next year, a 4-win team should average around 6.5, and a 12-win team should average around 10). The number highlighted in blue tells you how important the previous season’s win’s are as a predictor: the higher the number, the more predictive.

So naturally the next thing to see is a breakdown of these numbers between the pre- and post-salary cap eras:

Again, these are not small sample-sets, and they both visually and numerically confirm that the salary-cap era has greatly increased parity: while there are still plenty of excellent and terrible teams overall, the better teams regress and the worse teams get better, faster. The equations after the split lead to the following predictions for 4, 8, and 12 win teams (rounded to the nearest .25):

W	Pre-SC	Post-SC
4	6.25	7
8	8.25	8
12	10.5	9.25

Yes, the difference in expected wins between a 4-win team and a 12-win team in the post-cap era is only just over 2 wins, down from over 4.

While this finding may be mildly interesting in its own right, sadly this entire endeavor was a complete and utter failure, as the graphs failed to support my hypothesis that the salary cap has made the difference for 1-15 teams specifically. As this is an uncapped season, however, I guess what’s bad news for me is good news for the Rams.

The Case for Dennis Rodman, Part 1/4 (a)—Rodman v. Jordan

For reasons which should become obvious shortly, I’ve split Part 1 of this series into sub-parts. This section will focus on rating Rodman’s accomplishments as a rebounder (in painstaking detail), while the next section(s) will deal with the counterarguments I mentioned in my original outline.

For the uninitiated, the main stat I will be using for this analysis is “rebound rate,” or “rebound percentage,” which represents the percentage of available rebounds that the player grabbed while he was on the floor. Obviously, because there are 10 players on the floor for any given rebound, the league average is 10%. The defensive team typically grabs 70-75% of rebounds overall, meaning the average rates for offensive and defensive rebounds are approximately 5% and 15% respectively. This stat is a much better indicator of rebounding skill than rebounds per game, which is highly sensitive to factors like minutes played, possessions per game, and team shooting and shooting defense. Unlike many other “advanced” stats out there, it also makes perfect sense intuitively (indeed, I think the only thing stopping it from going completely mainstream is that the presently available data can technically only provide highly accurate “estimates” for this stat. When historical play-by-play data becomes more widespread, I predict this will become a much more popular metric).

Dennis Rodman has dominated this stat like few players have dominated any stat. For overall rebound % by season, not only does he hold the career record, he led the league 8 times, and holds the top 7 spots on the all-time list (red bars are Rodman):

^{Note this chart only goes back as far as the NBA/ABA merger in 1976, but going back further makes no difference for the purposes of this argument. As I will explain in my discussion of the “Wilt Chamberlain and Bill Russell Were Rebounding Gods” myth, the rebounding rates for the best rebounders tend to get worse as you go back in time, especially before Moses Malone.}
As visually impressive as that chart may seem, it is only the beginning of the story. Obviously we can see that the Rodman-era tower is the tallest in the skyline, but our frame of reference is still arbitrary: e.g., if the bottom of the chart started at 19 instead of 15, his numbers would look even more impressive. So one thing we can do to eliminate bias is put the average in the middle, and count percentage points above or below, like so:

With this we get a better visual sense of the relative greatness of each season. But we’re still left with percentage points as our unit of measurement, which is also arbitrary: e.g., how much better is “6%” better? To answer this question, in addition to the average, we need to calculate the standard deviation of the sample (if you’re normally not comfortable working with standard deviations, just think of them as standardized units of measurement that can be used to compare stats of different types, such as shooting percentages against points per game). Then we re-do the graph using standard deviations above or below the mean, like so:

^{Note this graph is actually exactly the same shape as the one above, it’s just compressed to fit on a scale from –3 to +8 for easy comparison with subsequent graphs. The SD for this graph is 2.35%.}
There is one further, major, problem with our graph: As strange as it may sound, Dennis Rodman’s own stats are skewing the data in a way that biases the comparison against him. Specifically, with the mean and standard deviation set where they are, Rodman is being compared to himself as well as to others. E.g., notice that most of the blue bars in the graph are below the average line: this is because the average includes Rodman. For most purposes, this bias doesn’t matter much, but Rodman is so dominant that he raises the league average by over a percent, and he is such an outlier that he alone nearly doubles the standard deviation. Thus, for the remaining graphs targeting individual players, I’ve calculated the average and standard deviations for the samples from the other players only:

^{Note that a negative number in this graph is not exactly a bad thing: that person still led the league in rebounding % that year. The SD for this graph is 1.22%.}
But not all rebounding is created equal: Despite the fact that they get lumped together in both conventional rebounding averages and in player efficiency ratings, offensive rebounding is worth considerably more than defensive rebounding. From a team perspective, there is not much difference (although not necessarily *no* difference – I suspect, though I haven’t yet proved, that possessions beginning with offensive rebounds have higher expected values than those beginning with defensive rebounds), but from an individual perspective, the difference is huge. This is because of what I call “duplicability”: simply put, if you failed to get a defensive rebound, there’s a good chance that your team would have gotten it anyway. Conversely, if you failed to get an offensive rebound, the chances of your team having gotten it anyway are fairly small. This effect can be very crudely approximated by taking the league averages for offensive and defensive rebounding, multiplying by .8, and subtracting from 1. The .8 comes from there being 4 other players on your team, and the subtraction from 1 gives you the value added for each rebound: The league averages are typically around 25% and 75%, so, very crudely, you should expect your team to get around 20% of the offensive and 60% of the defensive rebounds that you don’t. Thus, each offensive rebound is adding about .8 rebounds to your team’s total, and each defensive rebound is adding about .4. There are various factors that can affect the exact values one way or the other, but on balance I think it is fair to assume that offensive rebounds are about twice as valuable overall.

To that end, I calculated an adjusted rebounding % for every player since 1976 using the formula (2ORB% + DRB%)/3, and then ran it through all of the same steps as above:

Mindblowing, really. But before putting this graph in context, a quick mathematical aside: If these outcomes were normally distributed, a 6 standard deviation event like Rodman’s 1994-1995 season would theoretically happen only about once every billion seasons. But because each data point on this chart actually represents a maximum of a large sample of (mostly) normally distributed seasonal rebounding rates, they should instead be governed by the Gumbel distribution for extreme values: this leads to a much more manageable expected frequency of approximately once every 400 years (of course, that pertains to the odds of someone like Rodman coming along in the first place; now that we’ve had Rodman, the odds of another one showing up are substantially higher). In reality, there are so many variables at play from era to era, season to season, or even team to team, that a probability model probably doesn’t tell us as much as we would like (also, though standard deviations converge fairly quickly, the sample size is relatively modest).

Rather than asking how abstractly probable or improbable Rodman’s accomplishments were, it may be easier to get a sense of his rebounding skill by comparing this result to results of the same process for other statistics. To start with, note that weighting the offensive rebounding more heavily cuts both ways for Rodman: after the adjustment, he only holds the top 6 spots in NBA history, rather than the top 7. On the other hand, he led the league in this category 10 times instead of 8, which is perfect for comparing him to another NBA player who led a major statistical category 10 times — Michael Jordan:

^{Red bars are Jordan. Mean and standard deviation are calculated from 1976, excluding MJ, as with Rodman above.}

As you can see, the data suggests that Rodman was a better rebounder than Jordan was a scorer. Of course, points per game isn’t a rate stat, and probably isn’t as reliable as rebounding %, but that cuts in Rodman’s favor. Points per game should be more susceptible to varying circumstances that lead to extreme values. Compare, say, to a much more stable stat, Hollinger’s player efficiency rating:

Actually, it is hard to find any significant stat where someone has dominated as thoroughly as Rodman. One of the closest I could find is John Stockton and the extremely obscure “Assist %” stat:

^{Red bars are Stockton, mean and SD are calculated from the rest.}

Stockton amazingly led the league in this category 15 times, though he didn’t dominate individual seasons to the extent that Rodman did. This stat is also somewhat difficult to “detangle” (another term/concept I will use frequently on this blog), since assists always involve more than one player. Regardless, though, this graph is the main reason John Stockton is (rightfully) in the Hall of Fame today. Hmm…

On Nate Silver on ESPN Umpire Study

I was just watching the Phillies v. Mets game on TV, and the announcers were discussing this Outside the Lines study about MLB umpires, which found that 1 in 5 “close” calls were missed over their 184 game sample. Interesting, right?

So I opened up my browser to find the details, and before even getting to ESPN, I came across this criticism of the ESPN story by Nate Silver of FiveThirtyEight, which knocks his sometimes employer for framing the story on “close calls,” which he sees as an arbitrary term, rather than something more objective like “calls per game.” Nate is an excellent quantitative analyst, and I love when he ventures from the murky world of politics and polling to write about sports. But, while the ESPN study is far from perfect, I think his criticism here is somewhat off-base ill-conceived.

The main problem I have with Nate’s analysis is that the study’s definition of “close call” is not as “completely arbitrary” as Nate suggests. Conversely, Nate’s suggested alternative metric – blown calls per game – is much more arbitrary than he seems to think.

First, in the main text of the ESPN.com article, the authors clearly state that the standard for “close” that they use is: “close enough to require replay review to determine whether an umpire had made the right call.” Then in the 2nd sidebar, again, they explicitly define “close calls” as “those for which instant replay was necessary to make a determination.” That may sound somewhat arbitrary in the abstract, but let’s think for a moment about the context of this story: Given the number of high-profile blown calls this season, there are two questions on everyone’s mind: “Are these umps blind?” and “Should baseball have more instant replay?” Indeed, this article mentions “replay” 24 times. So let me be explicit where ESPN is implicit: This study is about instant replay. They are trying to assess how many calls per game could use instant replay (their estimate: 1.3), and how many of those reviews would lead to calls being overturned (their estimate: 20%).

Second, what’s with a quantitative (sometimes) sports analyst suddenly being enamored with per-game rather than rate-based stats? Sure, one blown call every 4 games sounds low, but without some kind of assessment of how many blown call opportunities there are, how would we know? In his post, Nate mentions that NBA insiders tell him that there were “15 or 20 ‘questionable’ calls” per game in their sport. Assuming ‘questionable’ means ‘incorrect,’ does that mean NBA referees are 60 to 80 times worse than MLB umpires? Certainly not. NBA refs may or may not be terrible, but they have to make double or even triple digit difficult calls every night. If you used replay to assess every close call in an NBA game, it would never end. Absent some massive longitudinal study comparing how often officials miss particular types of calls from year to year or era to era, there is going to be a subjective component when evaluating officiating. Measuring by performance in “close” situations is about as good a method as any.

Which is not to say that the ESPN metric couldn’t be improved: I would certainly like to see their guidelines for figuring out whether a call is review-worthy or not. In a perfect world, they might even break down the sets of calls by various proposals for replay implementation. As a journalistic matter, maybe they should have spent more time discussing their finding that only 1.3 calls per game are “close,” as that seems like an important story in its own right. On balance, however, when it comes to the two main issues that this study pertains to (the potential impact of further instant replay, and the relative quality of baseball officiating), I think ESPN’s analysis is far more probative than Nate’s.