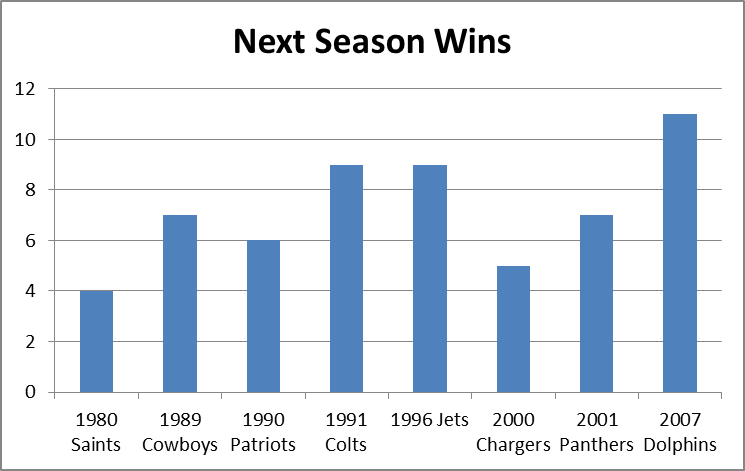
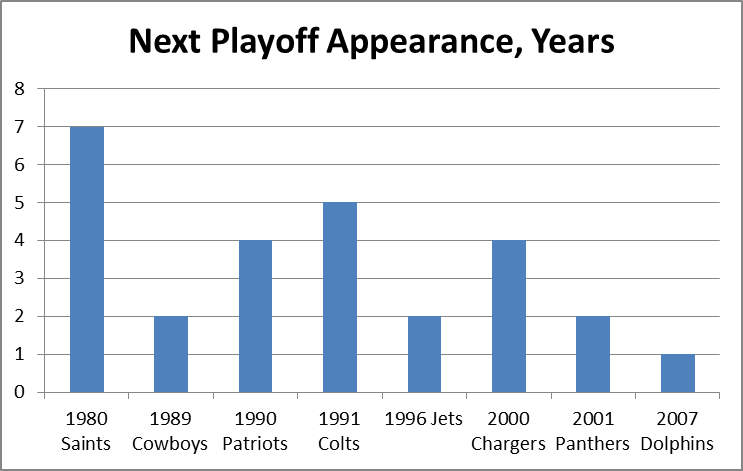
It is a quirky little fact that 1-15 teams have tended to bounce back fairly well. Since expanding to 16 games in 1978, 9 teams have hit the ignoble mark, including last year’s St. Louis Rams. Of the 8 that did it prior to 2009, all but the 1980 Saints made it back to the playoffs within 5 years, and 4 of the 8 eventually went on to win Super Bowls, combining for 8 total. The median number of wins for a 1-15 team in their next season is 7:
My grand hypothesis about this was that the implementation of the salary cap after the 1993-94 season, combined with some of the advantages I discuss below (especially 2 and 3), has been a driving force behind this small-but-sexy phenomenon: note that at least for these 8 data points, there seems to be an upward trend for wins and downward trend for years until next playoff appearance. Obviously, this sample is way too tiny to generate any conclusions, but before looking at harder data, I’d like to speculate a bit about various factors that could be at play. In addition to normally-expected regression to the mean, the chain of consequences resulting from being horrendously bad is somewhat favorable:
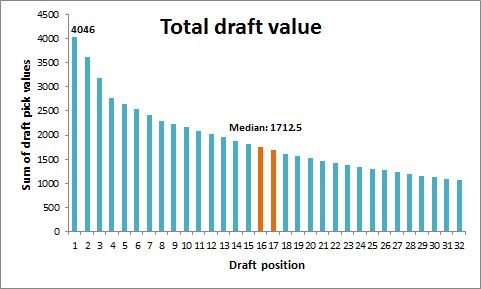
- The primary advantages are explicitly structural: Your team picks at the top of each round in the NFL draft. According to ESPN’s “standard” draft-pick value chart, the #1 spot in the draft is worth over twice as much as the 16th pick [side note: I don’t actually buy this chart for a second. It massively overvalue 1st round picks and undervalues 2nd round picks, particularly when it comes to value added (see a good discussion here)]:
- The other primary benefit, at least for one year, comes from the way the NFL sets team schedules: 14 games are played in-division and against common divisional opponents, but the last two games are set between teams that finished in equal positions the previous year (this has obviously changed many times, but there have always been similar advantages). Thus, a bottom-feeder should get a slightly easier schedule, as evidenced by the Rams having the 2nd-easiest schedule for this coming season.
- There are also reliable secondary benefits to being terrible, some of which get greater the worse you are. A huge one is that, because NFL statistics are incredibly entangled (i.e., practically every player on the team has an effect on every other player’s statistics), having a bad team tends to drag everyone’s numbers down. Since the sports market – and the NFL’s in particular – is stats-based on practically every level, this means you can pay your players less than what they’re worth going forward. Under the salary cap, this leaves you more room to sign and retain key players, or go for quick fixes in free agency (which is generally unwise, but may boost your performance for a season or two).
- A major tertiary effect – one that especially applies to 1-15 teams, is that embarrassed clubs tend to “clean house,” meaning, they fire coaches, get rid of old and over-priced veterans, make tough decisions about star players that they might not normally be able to make, etc. Typically they “go young,” which is advantageous not just for long-term team-building purposes, but because young players are typically the best value in the short term as well.
- An undervalued quaternary effect is that new personnel and new coaching staff, in addition to hopefully being better at their jobs than their predecessors, also make your team harder to prepare for, just by virtue of being new (much like the “backup quarterback effect,” but for your whole team).
- A super-important quinary effect is that. . . Ok, sorry, I can’t do it.
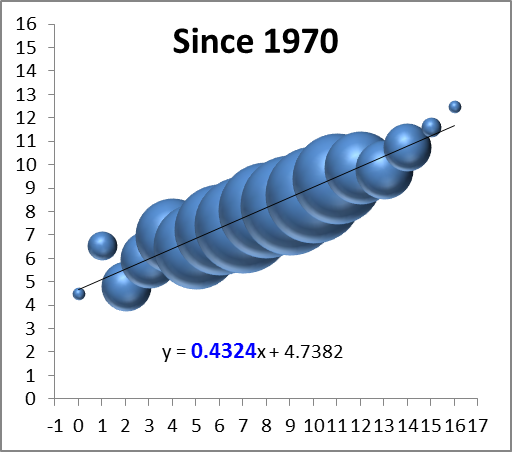
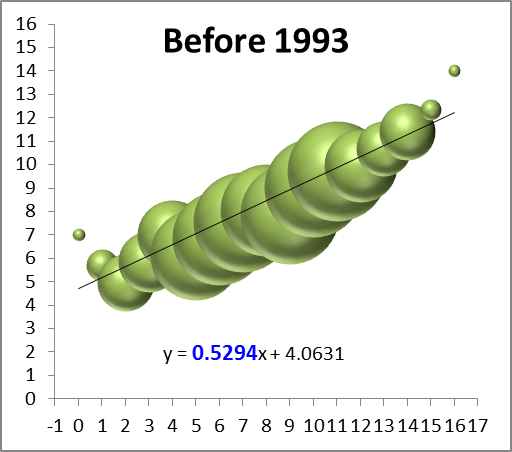
Of course, most of these effects are relevant to more than just 1-15 teams, so perhaps it would be better to expand the inquiry a tiny bit. For this purpose, I’ve compiled the records of every team since the merger, so beginning in 1970, and compared them to their record the following season (though it only affects one data point, I’ve treated the first Ravens season as a Browns season, and treated the new Browns as an expansion team). I counted ties as .5 wins, and normalized each season to 16 games (and rounded). I then grouped the data by wins in the initial season and plotted it on a “3D Bubble Chart.” This is basically a scatter-plot where the size of each data-point is determined by the number of examples (e.g., only 2 teams have gone undefeated, so the top-right bubble is very small). The 3D is not just for looks: the size of each sphere is determined by using the weights for volume, which makes it much less “blobby” than 2D, and it allows you to see the overlapping data points instead of just one big ink-blot:
*Note: again, the x-axis on this graph is wins in year n, and the y axis is wins in year n+1. Also, note that while there are only 16 “bubbles,” they represent well over a thousand data points, so this is a fairly healthy sample.
The first thing I can see is that there’s a reasonably big and fat outlier there for 1-15 teams (the 2nd bubble from the left)! But that’s hardly a surprise considering we started this inquiry knowing that group had been doing well, and there are other issues at play: First, we can see that the graph is strikingly linear. The equation at the bottom means that to predict a team’s wins for one year, you should multiply their previous season’s win total by ~.43 and add ~4.7 (e.g.’s: an 8-win team should average about 8 wins the next year, a 4-win team should average around 6.5, and a 12-win team should average around 10). The number highlighted in blue tells you how important the previous season’s win’s are as a predictor: the higher the number, the more predictive.
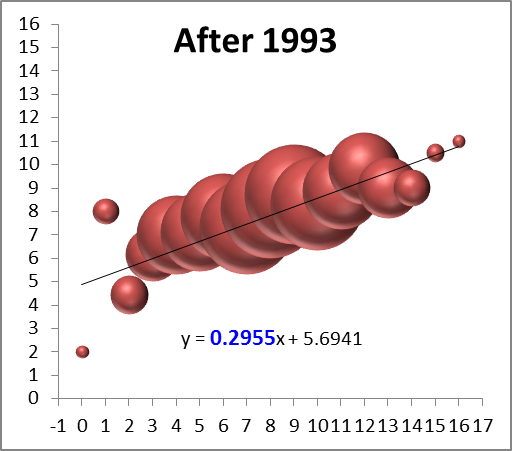
So naturally the next thing to see is a breakdown of these numbers between the pre- and post-salary cap eras:
Again, these are not small sample-sets, and they both visually and numerically confirm that the salary-cap era has greatly increased parity: while there are still plenty of excellent and terrible teams overall, the better teams regress and the worse teams get better, faster. The equations after the split lead to the following predictions for 4, 8, and 12 win teams (rounded to the nearest .25):
| W | Pre-SC | Post-SC |
| 4 | 6.25 | 7 |
| 8 | 8.25 | 8 |
| 12 | 10.5 | 9.25 |
While this finding may be mildly interesting in its own right, sadly this entire endeavor was a complete and utter failure, as the graphs failed to support my hypothesis that the salary cap has made the difference for 1-15 teams specifically. As this is an uncapped season, however, I guess what’s bad news for me is good news for the Rams.
Very interesting analysis, love the blog!
I still don’t understand what makes 1-15 teams *more special* than 0-16 teams or 2-14 teams. All four of the effects you outline should still be present for teams with 0 or 2 wins, should they not? Then why, in the first bubble graph (with the blue color), are 1-15 teams well above the fitted line? Do they make more coaching changes than teams with 0 or 2 wins? Do they make better draft picks?
That’s a question with a surprisingly complicated answer.
First the major difference for 0-16 teams is that there is no floor to their badness. Going 1-15 is much, much more likely than going 0-16, especially considering that 1-15 teams are almost always running really badly anyway (meaning, their true expectation per game is likely way above 1/16). There’s a whole Bayes’ Theorem thing behind it, but put simply: 0-16 teams, on average, are probably much worse than 1-15 teams. So the advantages are still there, but their starting point is much lower on average.
As for 2-14 teams, etc: yes, particularly if they finish last in the league, all of the same effects should come into play, but each to a lesser degree. So if you think of the outcome as a product of the different factors, even a small difference — if present in all of them — can compound into a big difference overall (think of exponents: .3^4 is 5 times larger than .2^4).
A broader study of such structural advantages is on my ultra-long-term agenda.