Tiger Woods is obviously having a terrible season. His scoring average so far (71.66) is almost 2 strokes higher than his previous worst year (69.75 in 1997). He has no wins, no top 3’s, and has only finished top 10 in 2 of 9 tournaments. That 22%, if it holds up, would be the worst of his career by 20%. For the first time basically ever, his eventually capturing the all-time major championships record is in doubt. Of course, 9 tournaments is not a large sample, and this could just be a slump. As I see it, there are basically 4 possibilities:
- Tiger is running very badly.
- Tiger is in serious decline.
- Tiger is declining somewhat and running somewhat badly.
- Tiger needs a shrink.
So the questions of the day are: a) How likely are each of these possibilities? and b) What does each say about his chances of winning 19 majors? For reasons I will explain, I believe 1 and 2 are very unlikely, and 3 is somewhat unlikely. Which is fine, since Tiger should basically pray this is all in his head, because otherwise his chances of catching and passing Nicklaus are diminishing considerably.
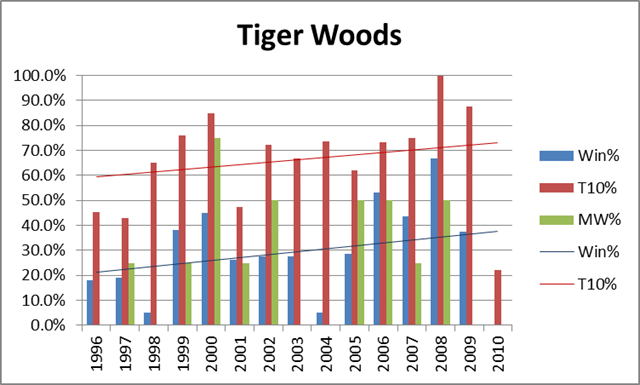
I would normally be the first to promote a “bad variance” explanation of this kind of phenomena, but in this case: a) Tiger doesn’t really have slumps like this; and b) the timing is too much of a coincidence. For some historical perspective, here’s a graph of Tiger’s overall winning %, top-10 finish %, and winning % in majors, by year:
For the record, his averages are 28.4%, 66.4% and 24.6%, respectively. As should be obvious, not only is his 2010 historically awful, but there is nothing to suggest that he was in decline beforehand. Despite having recently run slightly worse in majors than he did in the early 2000’s, his Win% and Top-10% trendlines have still been sloping upwards.
Of course, 2/3 of a season is still a small sample, and it is certainly possible that this is variance, but just because something *could* be a statistical artifact doesn’t mean that it is *likely* to be. In fact, one problem with statistically-oriented sports analysis is that its proponents can sometimes be overly (even dogmatically) committed to neutral or variance-based explanations for observed anomalies, even when the conventional explanation is highly plausible (ironically, I think this happens because people often apply Bayes’ Theorem-style reasoning implicitly, even if the statisticians forget to apply it explicitly). I believe this is one of those situations.
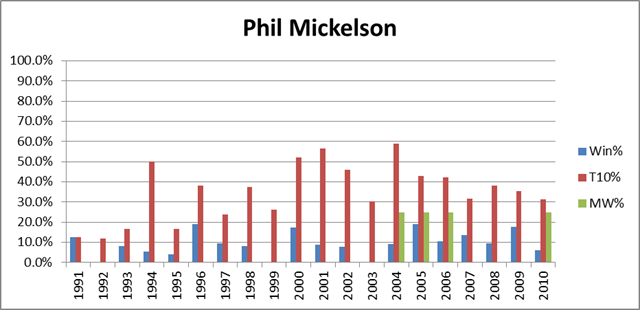
That said, whether it stems from diminishing skills or ongoing psychological unrest, a significant and continuing Tiger decline is still a realistic possibility. From the chart above, it should be clear that Tiger circa 2009 shouldn’t have any problem blowing past Jack, but what would happen if he were a different Tiger? Fortunately for him, he has a long way to drop before being a non-factor. For comparison, let’s look at the same graph as above, but for the 2nd-best player of the recent era, Phil Mickelson:
Mickleson’s averages are 9.2%, 35.8%, and 5.6%, respectively. Half a Tiger would still be much better. Of course, Mickelson has won 4 majors in recent years, but has still been much worse than Tiger: over that period his averages are 12.2%, 40.1%, and 14.3%. It should not go without notice that if Tiger transformed into Phil Mickelson, played 7 more years, and won majors at the same rate that Mickelson has over the last 7 (Phil is about 6 years older), it would put him at exactly the magic number: 18.
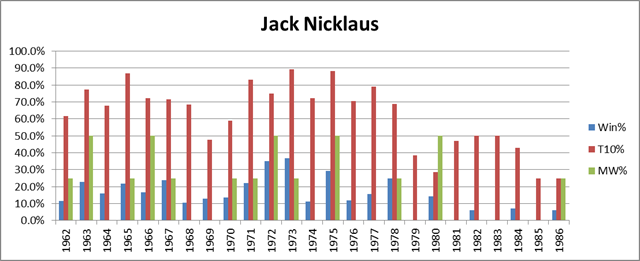
Finally, let’s look at the graph for the man himself — Jack Nicklaus:
Note: For years prior to 1970, only official PGA Tour events are included.
Jack’s averages over this span (from the year he turned pro to the year of his final major) are 15.5%, 63.4%, and 18%. These numbers are slightly understated, since in truth Jack was well past his prime when he won the Masters in ’86. As we can see, Jack began to decline significantly around 1979, but still won 3 more majors after that point. A similar pattern for Woods would put him at 17, and at least in contention for the record. On the other hand, not everyone is Jack Nicklaus. Nicklaus, incredibly, won a higher percentage of majors than tournaments overall. This is especially apparent in his post-decline career: note the small amount of blue compared to the amount of green from 1979 on. Whether he just ran well in the right spots, or whether he had preternatural competitive spirit, not even Tiger Woods can count on having Nicklaus’s knack for winning majors. So if Tiger hopes to catch up, he had better be out of his mind.