Applied Epistemology in Politics and the Playoffs

Two nights ago, as I was watching cable news and reading various online articles and blog posts about Christine O’Donnell’s upset win over Michael Castle in Delaware’s Republican Senate primary, the hasty, almost ferocious emergence of consensus among the punditocracy – to wit, that the GOP now has virtually zero chance of picking up that seat in November – reminded me of an issue that I’ve wanted to blog about since long before I began blogging in earnest: NFL playoff prediction models.

Specifically, I have been critical of those models that project the likelihood of each surviving team winning the Super Bowl by applying a logistic regression model (i.e., “odds of winning based on past performance”) to each remaining game. In January, I posted a number of comments to this article on Advanced NFL Stats, in which I found it absurd that, with 8 teams left, his model predicted that the Dallas Cowboys had about the same chance of winning the Super Bowl as the Jets, Ravens, Vikings, and Cardinals combined. In the brief discussion, I gave two reasons (in addition to my intuition): first, that these predictions were wildly out of whack with contract prices in sports-betting markets, and second, that I didn’t believe the model sufficiently accounted for “variance in the underlying statistics.” Burke suggested that the first point is explained by a massive epidemic of conjunction-fallacyitis among sports bettors. On its face, I think this is a ridiculous explanation: i.e., does he really believe that the market-movers in sports betting — people who put up hundreds of thousands (if not millions) of dollars of their own money — have never considered multiplying the odds of several games together? Regardless, in this post I will put forth a much better explanation for this disparity than either of us proffered at the time, hopefully mooting that discussion. On my second point, he was more dismissive, though I was being rather opaque (and somehow misspelled “beat” in one reply), so I don’t blame him. However, I do think Burke’s intellectual hubris regarding his model (aka “model hubris”) is notable – not because I have any reason to think Burke is a particularly hubristic individual, but because I think it is indicative of a massive epidemic of model-hubrisitis among sports bloggers.

In Section 1 of this post, I will discuss what I personally mean by “applied epistemology” (with apologies to any actual applied epistemologists out there) and what I think some of its more-important implications are. In Section 2, I will try to apply these concepts by taking a more detailed look at my problems with the above-mentioned playoff prediction models.

Section 1: Applied Epistemology Explained, Sort Of

For those who might not know, “epistemology” is essentially a fancy word for the “philosophical study of knowledge,” which mostly involves philosophers trying to define the word “knowledge” and/or trying to figure out what we know (if anything), and/or how we came to know it (if we do). For important background, read my Complete History of Epistemology (abridged), which can be found here: In Plato’s Theaetetus, Socrates suggests that knowledge is something like “justified true belief.” Agreement ensues. In 1963, Edmund Gettier suggests that a person could be justified in believing something, but it could be true for the wrong reasons. Debate ensues. The End.

A “hot” topic in the field recently has been dealing with the implications of elaborate thought experiments similar to the following:

*begin experiment*
Imagine yourself in the following scenario: From childhood, you have one burning desire: to know the answer to Question X. This desire is so powerful that you dedicate your entire life to its pursuit. You work hard in school, where you excel greatly, and you master every relevant academic discipline, becoming a tenured professor at some random elite University, earning multiple doctorates in the process. You relentlessly refine and hone your (obviously considerable) reasoning skills using every method you can think of, and you gather and analyze every single piece of empirical data relevant to Question X available to man. Finally, after decades of exhaustive research and study, you have a rapid series of breakthroughs that lead you to conclude – not arbitrarily, but completely based on the proof you developed through incredible amounts of hard work and ingenuity — that the answer to Question X is definitely, 100%, without a doubt: 42. Congratulations! To celebrate the conclusion of this momentous undertaking, you decide to finally get out of the lab/house/library and go celebrate, so you head to a popular off-campus bar. You are so overjoyed about your accomplishment that you decide to buy everyone a round of drinks, only to find that some random guy — let’s call him Neb – just bought everyone a round of drinks himself. What a joyous occasion: two middle-aged individuals out on the town, with reason to celebrate (and you can probably see where this is going, but I’ll go there anyway)! As you quickly learn, it turns out that Neb is around your same age, and is also a professor at a similarly elite University in the region. In fact, it’s amazing how much you two have in common: you have relatively similar demographic histories, identical IQ, SAT, and GRE scores, you both won multiple academic awards at every level, you have both achieved similar levels of prominence in your academic community, and you have both been repeatedly published in journals of comparable prestige. In fact, as it turns out, you have both been spent your entire lives studying the same question! You have both read all the same books, you have both met, talked or worked with many comparably intelligent — or even identical — people: It is amazing that you have never met! Neb, of course, is feeling so celebratory because finally, after decades of exhaustive research and study, he has just had a rapid series of breakthroughs that lead him to finally conclude – not arbitrarily, but completely based on the proof he developed through incredible amounts of hard work and ingenuity — that the answer to Question X is definitely, 100%, without a doubt: 54.

You spend the next several hours drinking and arguing about Question X: while Neb seemed intelligent enough at first, everything he says about X seems completely off base, and even though you make several excellent points, he never seems to understand them. He argues from the wrong premises in some areas, and draws the wrong conclusions in others. He massively overvalues many factors that you are certain are not very important, and is dismissive of many factors that you are certain are crucial. His arguments, though often similar in structure to your own, are extremely unpersuasive and don’t seem to make any sense, and though you try to explain yourself to him, he stubbornly refuses to comprehend your superior reasoning. The next day, you stumble into class, where your students — who had been buzzing about your breakthrough all morning — begin pestering you with questions about Question X and 42. In your last class, you had estimated that the chances of 42 being “the answer” were around 90%, and obviously they want to know if you have finally proved 42 for certain, and if not, how likely you believe it is now. What do you tell them?

All of the research and analysis you conducted since your previous class had, indeed, led you to believe that 42 is a mortal lock. In the course of your research, everything you have thought about or observed or uncovered, as well as all of the empirical evidence you have examined or thought experiments you have considered, all lead you to believe that 42 is the answer. As you hesitate, your students wonder why, even going so far as to ask, “Have you heard any remotely persuasive arguments against 42 that we should be considering?” Can you, in good conscience, say that you know the answer to Question X? For that matter, can you even say that the odds of 42 are significantly greater than 50%? You may be inclined, as many have been, to “damn the torpedoes” and act as if Neb’s existence is irrelevant. But that view is quickly rebutted: Say one of your most enterprising students brings a special device to class: when she presses the red button marked “detonate,” if the answer to Question X is actually 42, the machine will immediately dispense $20 bills for everyone in the room; but if the answer is not actually 42, it will turn your city into rubble. And then it will search the rubble, gather any surviving puppies or kittens, and blend them.

So assuming you’re on board that your chance encounter with Professor Neb implies that, um, you might be wrong about 42, what comes next? There’s a whole interesting line of inquiry about what the new likelihood of 42 is and whether anything higher than 50% is supportable, but that’s not especially relevant to this discussion. But how about this: Say the scenario proceeds as above, you dedicate your life, yadda yadda, come to be 100% convinced of 42, but instead of going out to a bar, you decide to relax with a bubble bath and a glass of Pinot, while Neb drinks alone. You walk into class the next day, and proudly announce that the new odds of 42 are 100%. Mary Kate pulls out her special money-dispensing device, and you say sure, it’s a lock, press the button. Yay, it’s raining Andrew Jacksons in your classroom! And then: **Boom** **Meow** **Woof** **Whirrrrrrrrrrrrrr**. Apparently Mary Kate had a twin sister — she was in Neb’s class.

*end experiment*

In reality, the fact that you might be wrong, even when you’re so sure you’re right, is more than a philosophical curiosity, it is a mathematical certainty. The processes that lead you to form beliefs, even extremely strong ones, are imperfect. And when you are 100% certain that a belief-generating process is reliable, the process that led you to that belief is likely imperfect. This line of thinking is sometimes referred to as skepticism — which would be fine if it weren’t usually meant as a pejorative.

When push comes to shove, people will usually admit that there is at least some chance they are wrong, yet they massively underestimate just what those chances are. In political debates, for example, people may admit that there is some miniscule possibility that their position is ill-informed or empirically unsound, but they will almost never say that they are more likely to be wrong than to be right. Yet, when two populations hold diametrically opposed views, either one population is wrong or both are – all else being equal, the correct assessment in such scenarios is that no-one is likely to have it right.

When dealing with beliefs about probabilities, the complications get even trickier: Obviously many people believe some things are close to 100% likely to be true, when the real probability may be some-much if not much-much lower. But in addition to the extremes, people hold a whole range of poorly-calibrated probabilistic beliefs, like believing something is 60% likely when it is actually 50% or 70%. (Note: Some Philosophically trained readers may balk at this idea, suggesting that determinism entails everything having either a 0 or 100% probability of being true. While this argument may be sound in classroom discussions, it is highly unpragmatic: If I believe that I will win a coin flip 60% of the time, it may be theoretically true that the universe has already determined whether the coin will turn up heads or tails, but for all intents and purposes, I am only wrong by 10%).

But knowing that we are wrong so much of the time doesn’t tell us much by itself: it’s very hard to be right, and we do the best we can. We develop heuristics that tend towards the right answers, or — more importantly for my purposes — that allow the consequences of being wrong in both directions even out over time. You may reasonably believe that the probability of something is 30%, when, in reality, the probability is either 20% or 40%. If the two possibilities are equally likely, then your 30% belief may be functionally equivalent under many circumstances, but they are not the same, as I will demonstrate in Section 2 (note to the philosophers: you may have noticed that this is a bit like the Gettier examples: you might be “right,” but for the wrong reasons).

There is a science to being wrong, and it doesn’t mean you have to mope in your study, or act in bad faith when you’re out of it. “Applied Epistemology” (at least as this armchair philosopher defines it) is the study of the processes that lead to knowledge and beliefs, and of the practical implications of their limitations.

Part 2: NFL Playoff Prediction Models

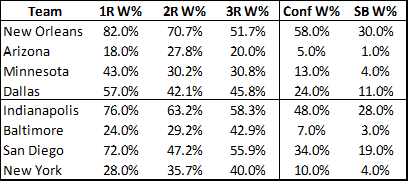
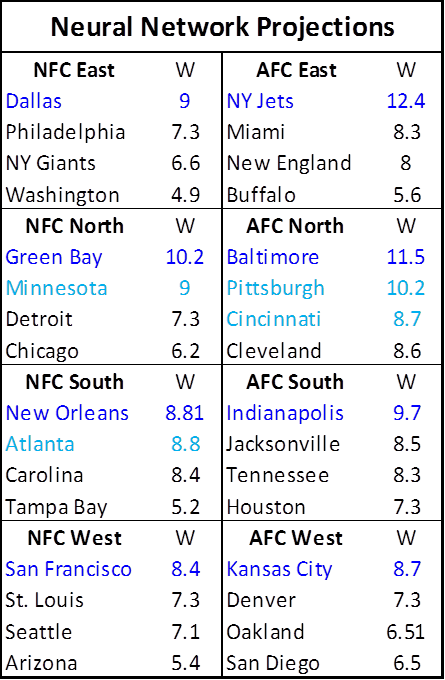
Now, let’s finally return to the Advanced NFL Stats playoff prediction model. Burke’s methodology is simple: using a logistic regression based on various statistical indicators, the model estimates a probability for each team to win their first round matchup. It then repeats the process for all possible second round matchups, weighting each by its likelihood of occurring (as determined by the first round projections) and so on through the championship. With those results in hand, a team’s chances of winning the tournament is simply the product of their chances of winning in each round. With 8 teams remaining in the divisional stage, the model’s predictions looked like this:

Burke states that the individual game prediction model has a “history of accuracy” and is well “calibrated,” meaning that, historically, of the teams it has predicted to win 30% of the time, close to 30% of them have won, and so on. For a number of reasons, I remain somewhat skeptical of this claim, especially when it comes to “extreme value” games where the model predicts very heavy favorites or underdogs. (E.g’s: What validation safeguards do they deploy to avoid over-fitting? How did they account for the thinness of data available for extreme values in their calibration method?) But for now, let’s assume this claim is correct, and that the model is calibrated perfectly: The fact that teams predicted to win 30% of the time actually won 30% of the time does NOT mean that each team actually had a 30% chance of winning.

That 30% number is just an average. If you believe that the model perfectly nails the actual expectation for every team, you are crazy. Since there is a large and reasonably measurable amount of variance in the very small sample of underlying statistics that the predictive model relies on, it necessarily follows that many teams will have significantly under or over-performed statistically relative to their true strength, which will be reflected in the model’s predictions. The “perfect calibration” of the model only means that the error is well-hidden.

This doesn’t mean that it’s a bad model: like any heuristic, the model may be completely adequate for its intended context. For example, if you’re going to bet on an individual game, barring any other information, the average of a team’s potential chances should be functionally equivalent to their actual chances. But if you’re planning to bet on the end-result of a series of games — such as in the divisional round of the NFL playoffs — failing to understand the distribution of error could be very costly.

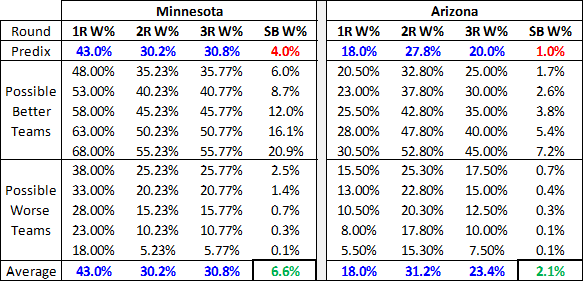
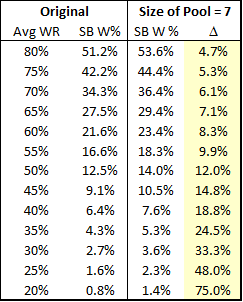
For example, let’s look at what happens to Minnesota and Arizona’s Super Bowl chances if we assume that the error in their winrates is uniformly distributed in the neighborhood of their predicted winrate:

For Minnesota, I created a pool of 11 possible expectations that includes the actual prediction plus teams that were 5% to 25% better or worse. I did the same for Arizona, but with half the deviation. The average win prediction for each game remains constant, but the overall chances of winning the Super Bowl change dramatically. To some of you, the difference between 2% and 1% may not seem like much, but if you could find a casino that would regularly offer you 100-1 on something that is actually a 50-1 shot, you could become very rich very quickly. Of course, this uniform distribution is a crude one of many conceivable ways that the “hidden error” could be distributed, and I have no particular reason to think it is more accurate than any other. But one thing should be abundantly clear: the winrate model on which this whole system rests tells us nothing about this distribution either.

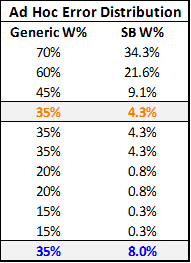
The exact structure of this particular error distribution is mostly an empirical matter that can and should invite further study. But for the purposes of this essay, speculation may suffice. For example, here is an ad hoc distribution that I thought seemed a little more plausible than a uniform distribution:

This table shows the chances of winning the Super Bowl for a generic divisional round playoff team with an average predicted winrate of 35% for each game. In this scenario, there is a 30% chance (3/10) that the prediction gets it right on the money, a 40% chance that the team is around half as good as predicted (the bottom 4 values), a 10% chance that the team is slightly better, a 10% chance that it is significantly better, and a 10% chance that the model’s prediction is completely off its rocker. These possibilities still produce a 35% average winrate, yet, as above, the overall chances of winning the Super Bowl increase significantly (this time by almost double). Of course, 2 random hypothetical distributions don’t yet indicate a trend, so let’s look at a family of distributions to see if we can find any patterns:

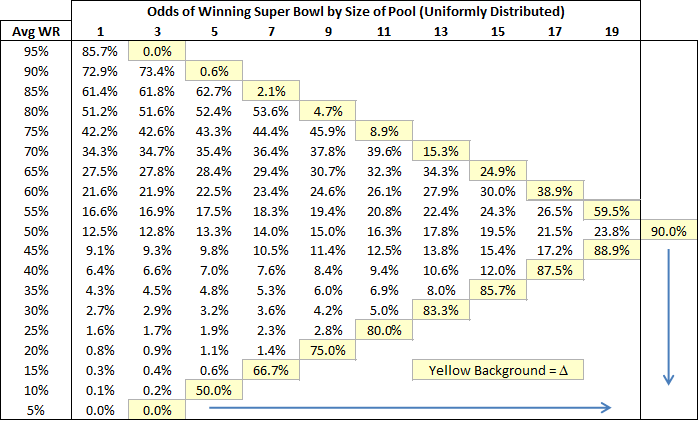
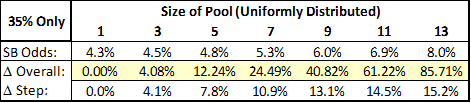
This chart compares the chances of a team with a given predicted winrate to win the Super Bowl based on uniform error distributions of various sizes. So the percentages in column 1 are the odds of the team winning the Super Bowl if the predicted winrate is exactly equal to their actual winrate. Then each subsequent column is the chances of them winning the Superbowl if you increase the “pool” of potential actual winrates by one on each side. Thus, the second number after 35% is the odds of winning the Super Bowl if the team is equally likely to be have a 30%, 35%, or 40% chance in reality, etc. The maximum possible change in Super Bowl winning chances for each starting prediction is contained in the light yellow box at the end of each row. I should note that I chose this family of distributions for its ease of cross-comparison, not its precision. I also experimented with many other models that produced a variety of interesting results, yet in every even remotely plausible one of them, two trends – both highly germane to my initial criticism of Burke’s model – endured:
1. Lower predicted game odds lead to greater disparity between predicted and actual chances.
To further illustrate this, here’s a vertical slice of the data, containing the net change for each possible prediction, given a discreet uniform error distribution of size 7:

2. Greater error ranges in the underlying distribution lead to greater disparity between predicted and actual chances.

To further illustrate this, here’s a horizontal slice of the data, containing the net change for each possible error range, given an initial winrate prediction of 35%:

Of course these underlying error distributions can and should be examined further, but even at this early stage of inquiry, we “know” enough (at least with a high degree of probability) to begin drawing conclusions. I.e., We know there is considerable variance in the statistics that Burke’s model relies on, which strongly suggests that there is a considerable amount of “hidden error” in its predictions. We know greater “hidden error” leads to greater disparity in predicted Super Bowl winning chances, and that this disparity is greatest for underdogs. Therefore, it is highly likely that this model significantly under-represents the chances of underdog teams at the divisional stage of the playoffs going on to win the Superbowl. Q.E.D.

This doesn’t mean that these problems aren’t fixable: the nature of the error distribution of the individual game-predicting model could be investigated and modeled itself, and the results could be used to adjust Burke’s playoff predictions accordingly. Alternatively, if you want to avoid the sticky business of characterizing all that hidden error, a Super-Bowl prediction model could be built that deals with that problem heuristically: say, by running a logistical regression that uses the available data to predict each team’s chances of winning the Super Bowl directly.

Finally, I believe this evidence both directly and indirectly supports my intuition that the large disparity between Burke’s predictions and the corresponding contract prices was more likely to be the result of model error than market error. The direct support should be obvious, but the indirect support is also interesting: Though markets can get it wrong just as much or more than any other process, I think that people who “put their money where their mouth is” (especially those with the most influence on the markets) tend to be more reliably skeptical and less dogmatic about making their investments than bloggers, analysts or even academics are about publishing their opinions. Moreover, by its nature, the market takes a much more pluralistic approach to addressing controversies than do most individuals. While this may leave it susceptible to being marginally outperformed (on balance) by more directly focused individual models or persons, I think it will also be more likely to avoid pitfalls like the one above.

Conclusions, and My Broader Agenda

The general purpose of post is to demonstrate both the importance and difficulty of understanding and characterizing the ways in which our beliefs – and the processes we use to form them — can get it wrong. This is, at its heart, a delicate but extremely pragmatic endeavor. It involves being appropriately skeptical of various conclusions — even when they seem right to you – and recognizing the implications of the multitude of ways that such error can manifest.

I have a whole slew of ideas about how to apply these principles when evaluating the various pronouncements made by the political commentariat, but the blogosphere already has a Nate Silver (and Mr. Silver is smarter than me anyway), so I’ll leave that for you to consider as you see fit.

Calculator: NFL/NCAA QB Ratings

Recently, I have been working very hard on some exciting behind-the-scenes upgrades for the blog. For example, I’ve been designing a number of web-mining processes to beef up my football and basketball databases, which should lead to more robust content in the future. I’ve also been working on an a much easier way to make interactive posts (without having to hard-code them or use plug-ins). My thinking is, if I lower the difficulty of creating interactive calculators and graph generators enough, then a collection of fun/interesting/useful resources should practically build itself.

To that end, I believe I have found the right tools to make moderately complex interactive charts and data out of spreadsheets, and I have been getting better and better at the process. As a test-run, however, let’s start with something simpler: A calculator for the much-maligned and nigh-impenetrable QB Ratings systems of the NFL and NCAA:

If all is working properly, the rating should re-calculate automatically whenever you change the data (i.e., no need to push a button), provided you have valid numbers in all 5 boxes. Please let me know if you have any difficulty viewing or using it.

From an analytical standpoint, there’s obviously not much to see here — though for certain values I am mildly surprised by the extreme disparity between the NFL and NCAA flavors.

Easy NFL Predictions, the SkyNet Way

In this post I briefly discussed regression to the mean in the NFL, as well as the difficulty one can face trying to beat a simple prediction model based on even a single highly probative variable. Indeed, for all the extensive research and cutting-edge analysis they conduct at Football Outsiders, they are seemingly unable to beat “Koko,” which is just about the simplest regression model known to primates.

Of course, since there’s no way I could out-analyze F.O. myself — especially if I wanted to get any predictions out before tonight’s NFL opener – I decided to let my computer do the work for me: this is what neural networks are all about. In case you’re not familiar, a neural network is a learning algorithm that can be used as a tool to process large quantities of data with many different variables — even if you don’t know which variables are the most important, or how they interact with each other.

The graphic to the right is the end result of several whole minutes of diligent configuration (after a lot of tedious data collection, of course). It uses 60 variables (which are listed under the fold below), though I should note that I didn’t choose them because of their incredible probative value – many are extremely collinear, if not pointless — I mostly just took what was available on the team and league summary pages on Pro Football Reference, and then calculated a few (non-advanced) rate stats and such in Excel.

Now, I don’t want to get too technical, but there are a few things about my methodology that I need to explain. First, predictive models of all types have two main areas of concern: under-fitting and over fitting. Football Outsiders, for example, creates models that “under fit” their predictions. That is to say, however interesting the individual components may be, they’re not very good at predicting what they’re supposed to. Honestly, I’m not sure if F.O. even checks their models against the data, but this is a common problem in sports analytics: the analyst gets so caught up designing their model a priori that they forget to check whether it actually fits the empirical data. On the other hand, to the diligent empirically-driven model-maker, overfitting — which is what happens when your model tries too hard to explain the data — can be just as pernicious. When you complicate your equations or add more and more variables, it gives your model more opportunity to find an “answer” that fits even relatively large data-sets, but which may not be nearly as accurate when applied elsewhere.

For example, to create my model, I used data from the introduction of the Salary Cap in 1994 on. When excluding seasons where a team had no previous or next season to compare to, this left me with a sample of 464 seasons. Even with a sample this large, if you include enough variables you should get good-looking results: a linear regression will appear to make “predictions” that would make any gambler salivate, and a Neural Network will make “predictions” that would make Nostradamus salivate. But when you take those models and try to apply them to new situations, the gambler and Nostradamus may be in for a big disappointment. This is because there’s a good chance your model is “overfit”, meaning it is tailored specifically to explain your dataset rather than to identifying the outside factors that the data-set reveals. Obviously it can be problematic if we simply use the present data to explain the present data. “Model validation” is a process (woefully ignored in typical sports analysis), by which you make sure that your model is capable of predicting data as well as explaining it. One of the simplest such methods is called “split validation.” This involves randomly splitting your sample in half, creating a “practice set” and a “test set,” and then deriving your model from the practice set while applying it to the test set. If “deriving” a model is confusing to you, think of it like this: you are using half of your data to find an explanation for what’s going on and then checking the other half to see if that explanation seems to work. The upside to this is that if your method of model-creating can pass this test reliably, your models should be just as accurate on new data as they are on the data you already have. The downside is that you have to cut your sample size in half, which leads to bigger swings in your results, meaning you have to repeat the process multiple times to be sure that your methodology didn’t just get lucky on one round.

For this model, the main method I am going to use to evaluate predictions is a simple correlation between predicted outcomes and actual outcomes. The dependent variable (or variable I am trying to predict), is the next season’s wins. As a baseline, I created a linear correlation against SRS, or “Simple Rating System,” which is PFR’s term for margin of victory adjusted for strength of schedule. This is the single most probative common statistic when it comes to predicting the next season’s wins, and as I’ve said repeatedly, beating a regression of one highly probative variable can be a lot of work for not much gain. To earn any bragging rights as a model-maker, I think you should be able to beat the linear SRS predictions by at least 5%, since that’s approximately the edge you would need to win money gambling against it in a casino. For further comparison, I also created a “Massive Linear” model, which uses the majority of the variables that go into the neural network (excluding collinear variables and variables that have almost no predictive value). For the ultimate test, I’ve created one model that is a linear regression using only the most probative variables, AND I allowed it to use the whole sample space (that is, I allowed it to cheat and use the same data that it is predicting to build its predictions). For my “simple” neural network, of course, I didn’t do any variable-weighting or analysis myself, and it required very little configuration: I used a very slow ‘learning rate’ (.025 if that means anything to you) with a very high number of learning cycles (5000), with decay on. For the validated models, I repeated this process about 20 times and averaged the outcomes. I have also included the results from running the data through the “Koko” model, and added results from the last 2 years of Football Outsiders predictions. As you will see, the neural network was able to beat the other models fairly handily:

^{Football Outsider numbers are obviously not since 1994. Note that Koko actually performs on par with F.O. overall, though both are pretty weak compared to the SRS regression or the cheat regression. “Koko” performed very well last season, posting a .560 correlation, though apparently last season was highly “predictable,” as all of the models based on previous patterns performed extremely well. Note also that the Massive Linear model performs poorly: this is as a result of overfitting, as explained above.}

Now here is where it gets interesting. When I first envisioned this post, I was planning to title it “Why I Don’t Make Predictions; And: Predictions!” — on the theory that, given the extreme variance in the sport, any highly-accurate model would probably produce incredibly boring results. That is, most teams would end up relatively close to the mean, and the “better” teams would normally just be the better teams from the year before. But when applied the neural network to the data for this season, I was extremely surprised by its apparent boldness:

^{I should note that the numbers will not add up perfectly as far as divisions and conferences go. In fact, I slightly adjusted them proportionally to make them fit the correct number of games for the league as a whole (which should have little or positive effect on its predictive power). SkyNet does not know the rules of football or the structure of the league, and its main goal is to make the most accurate predictions on a team by team basis, and then destroy humanity.}

Wait, what? New Orleans struggling to make the playoffs? Oakland with a better record than San Diego? The Jets as the league’s best team? New England is out?!? These are not the predictions of a milquetoast forecaster, so I am pleased to see that my simple creation has gonads. Of course there is obviously a huge amount of variance in this process, and a .43 correlation still leaves a lot to chance. But just to be completely clear, this is exactly the same model that soundly beat Koko, Football Outsiders, and several reasonable linear regressions — some of which were allowed to cheat – over the past 15 years. In my limited experience, neural networks are often capable of beating conventional models even when they produce some bizarre outcomes: For example, one of my early NBA playoff wins-predicting neural networks was able to beat most linear regressions by a similar (though slightly smaller) margin, even though it predicted negative wins for several teams. Anyway, I look forward to seeing how the model does this season. Though, in my heart of hearts, if the Jets win the Super Bowl, I may fear for the future of mankind.

A list of all the input variables, after the jump:

Read the rest of this entry »

Quantum Randy Moss—An Introduction to Entanglement

[Update: This post from 2010 has been getting some renewed attention in response to Randy Moss’s mildly notorious statement in New Orleans. I’ve posted a follow-up with more recent data here: “Is Randy Moss the Greatest?” For discussion of the broader idea, however, you’re in the right place.]

As we all know, even the best-intentioned single-player statistical metrics will always be imperfect indicators of a player’s skill. They will always be impacted by external factors such as variance, strength of opponents, team dynamics, and coaching decisions. For example, a player’s shooting % in basketball is a function of many variables – such as where he takes his shots, when he takes his shots, how often he is double-teamed, whether the team has perimeter shooters or big space-occupying centers, how often his team plays Oklahoma, etc – only one of which is that player’s actual shooting ability. Some external factors will tend to even out in the long-run (like opponent strength in baseball). Others persist if left unaccounted for, but are relatively easy to model (such as the extra value of made 3 pointers, which has long been incorporated into “true shooting percentage”). Some can be extremely difficult to work with, but should at least be possible to model in theory (such as adjusting a running back’s yards per carry based on the run-blocking skill of their offensive line). But some factors can be impossible (or at least practically impossible) to isolate, thus creating systematic bias that cannot be accurately measured. One of these near-impossible external factors is what I call “entanglement,” a phenomenon that occurs when more than one player’s statistics determine and depend on each other. Thus, when it comes to evaluating one of the players involved, you run into an information black hole when it comes to the entangled statistic, because it can be literally impossible to determine which player was responsible for the relevant outcomes.

While this problem exists to varying degrees in all team sports, it is most pernicious in football. As a result, I am extremely skeptical of all statistical player evaluations for that sport, from the most basic to the most advanced. For a prime example, no matter how detailed or comprehensive your model is, you will not be able to detangle a quarterback’s statistics from those of his other offensive skill position players, particularly his wide receivers. You may be able to measure the degree of entanglement, for example by examining how much various statistics vary when players change teams. You may even be able to make reasonable inferences about how likely it is that one player or another should get more credit, for example by comparing the careers of Joe Montana with Kansas City and Jerry Rice with Steve Young (and later Oakland), and using that information to guess who was more responsible for their success together. But even the best statistics-based guess in that kind of scenario is ultimately only going to give you a probability (rather than an answer), and will be based on a miniscule sample.

Of course, though stats may never be the ultimate arbiter we might want them to be, they can still tell us a lot in particular situations. For example, if only one element (e.g., a new player) in a system changes, corresponding with a significant change in results, it may be highly likely that that player deserves the credit (note: this may be true whether or not it is reflected directly in his stats). The same may be true if a player changes teams or situations repeatedly with similar outcomes each time. With that in mind, let’s turn to one of the great entanglement case-studies in NFL history: Randy Moss.
I’ve often quipped to my friends or other sports enthusiasts that I can prove that Randy Moss is probably the best receiver of all time in 13 words or less. The proof goes like this:

Chad Pennington, Randall Cunningham, Jeff George, Daunte Culpepper, Tom Brady, and Matt Cassell.

The entanglement between QB and WR is so strong that I don’t think I am overstating the case at all by saying that, while a receiver needs a good quarterback to throw to him, ultimately his skill-level may have more impact on his quarterback’s statistics than on his own. This is especially true when coaches or defenses key on him, which may open up the field substantially despite having a negative impact on his stat-line. Conversely, a beneficial implication of such high entanglement is that a quarterback’s numbers may actually provide more insight into a wide receiver’s abilities than the receiver’s own – especially if you have had many quarterbacks throwing to the same receiver with comparable success, as Randy Moss has.

Before crunching the data, I would like to throw some bullet points out there:

There have been 6 quarterbacks who have started 9 or more games in a season with Randy Moss as one of their receivers (for obvious reasons, I have replaced Chad Pennington with Kerry Collins for this analysis).
Only two of them had starting jobs in the seasons immediately prior to those with Moss (Kerry Collins, Tom Brady).
Only one of them had a starting job in the season immediately following those with Moss (Matt Cassell).
Pro Bowl appearances of quarterbacks throwing to Moss: 6. Pro-Bowl appearances of quarterbacks after throwing to Moss: 0.
Daunte Culpepper made the Pro Bowl 3 times in his 5 seasons throwing to Moss. He has won a combined 5 games as a starting quarterback in 5 seasons since.

With the exception of Kerry Collins, all of the QB’s who have thrown to Moss have had “career” years with him (Collins improved, but not by as much at the others). To illustrate this point, I’ve compiled a number of popular statistics for each quarterback for their Moss years and their other years, in order to figure out the average affect Moss has had. To qualify as a “Moss year,” they had to have been his quarterback for at least 9 games. I have excluded all seasons where the quarterback was primarily a reserve, or was only the starting quarterback for a few games. The “other” seasons include all of that QB’s data in seasons without Moss on his team. This is not meant to bias the statistics, the reason I exclude partial seasons in one case and not the other is that I don’t believe occasional sub work or participation in a QB controversy accurately reflects the benefit of throwing to Moss, but those things reflect the cost of not having Moss just fine. In any case, to be as fair as possible, I’ve included the two Daunte Culpepper seasons where he was seemingly hampered by injury, and the Kerry Collins season where Oakland seemed to be in turmoil, all three of which could arguably not be very representative.

As you can see in the table below, the quarterbacks throwing to Moss posted significantly better numbers across the board:

_{[Edit to note: in this table’s sparklines and in the charts below, the 2nd and third positions are actually transposed from their chronological order. Jeff George was Moss’s 2nd quarterback and Culpepper was his 3rd, rather than vice versa. This happened because I initially sorted the seasons by year and team, forgetting that George and Culpepper both came to Minnesota at the same time.]}

^{Note: Adjusted Net Yards Per Attempt incorporates yardage lost due to sacks, plus gives bonuses for TD’s and penalties for interceptions. Approximate Value is an advanced stat from Pro Football Reference that attempts to summarize all seasons for comparison across positions. Details here.}

Out of 60 metrics, only 3 times did one of these quarterbacks fail to post better numbers throwing to Moss than in the rest of his career: Kerry Collins had a slightly lower completion percentage and slightly higher sack percentage, and Jeff George had a slightly higher interception percentage for his 10-game campaign in 1999 (though this was still his highest-rated season of his career). For many of these stats, the difference is practically mind-boggling: QB Rating may be an imperfect statistic overall, but it is a fairly accurate composite of the passing statistics that the broader football audience cares the most about, and 19.8 points is about the difference in career rating between Peyton Manning and J.P. Losman.

Though obviously Randy Moss is a great player, I still maintain that we can never truly measure exactly how much of this success was a direct result of Moss’s contribution and how much was a result of other factors. But I think it is very important to remember that, as far as highly entangled statistics like this go, independent variables are rare, and this is just about the most robust data you’ll ever get. Thus, while I can’t say for certain that Randy Moss is the greatest receiver in NFL History, I think it is unquestionably true that there is more statistical evidence of Randy Moss’s greatness than there is for any other receiver.

Full graphs for all 10 stats after the jump:

Read the rest of this entry »

Graph of the Day 2: NFL Regression—Descent Into Chaos

I guess it’s funky graph day here at SSA:
This one corresponds to the bubble-graphs in this post about regression to the mean before and after the introduction of the salary cap. Each colored ball represents one of the 32 teams, with wins in year n on the x axis and wins in year n+1 on the y axis. In case you don’t find the visual interesting enough in its own right, you’re supposed to notice that it gets crazier right around 1993.

Graph of the Day: Rodman, Visualized—An Outlier in Motion

(Just press play.)

The Case for Dennis Rodman, Part 1/4 (c)—Rodman v. Ancient History

One of the great false myths in basketball lore is that Wilt Chamberlain and Bill Russell were Rebounding Gods who will never be equaled, and that dominant rebounders like Dennis Rodman should count their blessings that they got to play in a era without those two deities on the court. This myth is so pervasive that it is almost universally referenced as a devastating caveat whenever sports commentators and columnists discuss Rodman’s rebounding prowess. In this section, I will attempt to put that caveat to death forever.

The less informed version of the “Chamberlain/Russell Caveat” (CRC for short) typically goes something like this: “Rodman led the league in rebounding 7 times, making him the greatest re bounder of his era, even though his numbers come nowhere near those of Chamberlain and Russell.” It is true that, barring some dramatic change in the way the game is played, Chamberlain’s record of 27.2 rebounds per game, set in the 1960-61 season, will stand forever. This is because, due to the fast pace and terrible shooting, the typical game in 1960-61 featured an average of 147 rebounding opportunities. During Rodman’s 7-year reign as NBA rebounding champion (from 1991-92 through 1997-98), the typical game featured just 84 rebounding opportunities. Without further inquiry, this difference alone means that Chamberlain’s record 27.2 rpg would roughly translate to 15.4 in Rodman’s era – over a full rebound less than Rodman’s ~16.7 rpg average over that span.

The slightly more informed (though equally wrong) version of the CRC is a plea of ignorance, like so: “Rodman has the top 7 rebounding percentages since the NBA started to keep the necessary statistics in 1970. Unfortunately, there is no game-by-game or individual opponent data prior to this, so it is impossible to tell whether Rodman was as good as Russell or Chamberlain” (this point also comes in many degrees of snarky, like, “I’ll bet Bill and Wilt would have something to say about that!!!”). We may not have the necessary data to calculate Russell and Chamberlain’s rebounding rates, either directly or indirectly. But, as I will demonstrate, there are quite simple and extremely accurate ways to estimate these figures within very tight ranges (which happen to come nowhere close to Dennis Rodman).

Before getting into rebounding percentages, however, let’s start with another way of comparing overall rebounding performance: Team Rebound Shares. Simply put, this metric is the percentage of team rebounds that were gotten by the player in question. This can be done for whole seasons, or it can be approximated over smaller periods, such as per-game or per-minute, even if you don’t have game-by-game data. For example, to roughly calculate the stat on a per-game basis, you can simply take a player’s total share of rebounds (their total rebounds/team’s total rebounds), and divide by the percentage of games they played (player gms/team gms). I’ve done this for all of Rodman, Russell and Chamberlain’s seasons, and organized the results as follows:

As we can see, Rodman does reasonably well in this metric, still holding the top 4 seasons and having a better average through 7. This itself is impressive, considering Rodman averaged about 35 minutes per game and Wilt frequently averaged close to 48.

I should note, in Chamberlain’s favor, that one of the problems I have with PER and its relatives is that they don’t give enough credit for being able to contribute extra minutes, as Wilt obviously could. However, since here I’m interested more in each player’s rebounding ability than in their overall value, I will use the same equation as above (plus dividing by 5, corresponding to the maximum minutes for each player) to break the team rebounding shares down by minute:

This is obviously where Rodman separates himself from the field, even pulling in >50% of his team’s rebounds in 3 different seasons. Of course, this only tells us what it tells us, and we’re looking for something else: Total Rebounding percentage. Thus, the question naturally arises: how predictive of TRB% are “minute-based team rebound shares”?

In order to answer this question, I created a slightly larger data-set, by compiling relevant full-season statistics from the careers of Dennis Rodman, Dwight Howard, Tim Duncan, David Robinson, and Hakeem Olajuwon (60 seasons overall). I picked these names to represent top-level rebounders in a variety of different situations (and though these are somewhat arbitrary, this analysis doesn’t require a large sample). I then calculated TRS by minute for each season and divided by 2 — roughly corresponding to the player’s share against 10 players instead of 5. Thus, all combined, my predictive variable is determined as follows:

$PV=\frac{Player Rebounds/Team Rebounds}{Player Minutes/Team Minutes}/10$

Note that this formula may have flaws as an independent metric, but if it’s predictive enough of the metric we really care about — Total Rebound % — those no longer matter. To that end, I ran a linear regression in Excel comparing this new variable to the actual values for TRB%, with the following output:

If you don’t know how to read this, don’t sweat it. The “R Square” of .98 pretty much means that our variable is almost perfectly predictive of TRB%. The two numbers under “Coefficients” tell us the formula we should use to make predictions based on our variable:

$Predicted TRB\% = 1.08983*PV - .01154$

Putting the two equations together, we have a model that predicts a player’s rebound percentage based on 4 inputs:

$TRB\% = 1.08983 * \frac{Player Rebounds/Team Rebounds}{Player Minutes/Team Minutes} /10 - .0115$

Now again, if you’re familiar with regression output, you can probably already see that this model is extremely accurate. But to demonstrate that fact, I’ve created two graphs that compare the predicted values with actual values, first for Dennis Rodman alone:

And then for the full sample:

So, the model seems solid. The next step is obviously to calculate the predicted total rebound percentages for each of Wilt Chamberlain and Bill Russell’s seasons. After this, I selected the top 7 seasons for each of the three players and put them on one graph (Chamberlain and Russell’s estimates vs. Rodman’s actuals):

It’s not even close. It’s so not close, in fact, that our model could be way off and it still wouldn’t be close. For the next two graphs, I’ve added error bars to the estimation lines that are equal to the single worst prediction from our entire sample (which was a 1.21% error, or 6.4% of the underlying number): [I should add a technical note, that the actual expected error should be slightly higher when applied to “outside” situations, since the coefficients for this model were “extracted” from the same data that I tested the model on. Fortunately, that degree of precision is not necessary for our purposes here.] First Rodman vs. Chamberlain:

Then Rodman vs. Russell:

In other words, if the model were as inaccurate in Russell and Chamberlain’s favor as it was for the worst data point in our data set, they would still be crushed. In fact, over these top 7 seasons, Rodman beats R&C by an average of 7.2%, so if the model understated their actual TRB% every season by 5 times as much as the largest single-season understatement in our sample, Rodman would still be ahead [edit: I’ve just noticed that Pro Basketball Reference has a TRB% listed for each of Chamberlain’s last 3 seasons. FWIW, this model under-predicts one by about 1%, over-predicts one by about 1%, and gets the third almost on the money (off by .1%)].

To stick one last dagger in CRC’s heart, I should note that this model predicts that Chamberlain’s best TRB% season would have been around 20.16%, which would rank 67th on the all-time list. Russell’s best of 20.08 would rank 72nd. Arbitrarily giving them 2% for the benefit of the doubt, their best seasons would still rank 22nd and 24th respectively.

This Week in Skeptical Sports Analysis

I’ve just returned from a weekend wedding getaway in NoCal, and I’m excited to get back to work on the blog. In this weekly feature (which will normally be posted on Sundays), I will post blog-related news, review some of the site activity from the previous week, give quick previews of what’s to come in the following week and what’s in the works, plus respond to any questions or requests.

Blog news:

There is now a sweet iPhone/mobile version of the blog, thanks to the WPTouch plug-in. To see it, just open the blog in any iPhone, Android, Blackberry or Palm Pre device.
I’ve added my Twitter feed to the right sidebar, using the Twitter Goodies plug-in. It works nicely, although it currently won’t display my re-tweets. If you happen to know how to fix this, please email me.
I added a “praise for Skeptical Sports” section to the “about this blog” page. By default, I assume that public statements of praise (e.g., from Twitter, in the comments, or on a public forum) are OK to duplicate there, but if for whatever reason you don’t want your statement to appear anymore, just let me know and I’ll remove it.
There’s a thread on 2+2 (a poker/gambling forum with an excellent sports section) about this blog that contains a decent amount of discussion about some of the topics I’ve posted on, especially Dennis Rodman and Carmello Anthony. It also includes some silly speculation about what my “secret identity” on 2+2 might be, but the sports analysis is interesting. Also, if any of those guys are reading, feel free to post in the comments here as well (and I don’t mind cross-posting).

Last week on the blog:

On Sunday, I posted an analysis of Tiger Woods’ horrible performance this year, focusing on whether it is consistent with a natural decline, and questioning what the consequences would be if the change is permanent.
On Monday I posted this criticism of Nate Silver criticizing an ESPN study about baseball umpiring.
On Tuesday and Friday I posted parts 1(a) and 1(b) of my Dennis Rodman series, both addressing the issue of just how good a rebounder he was.
On Wednesday I posted an article ostensibly about the 1-15 St. Louis Rams, which was really an attempt to quantify the effects of the salary cap on regression to the mean in the NFL.
On Thursday I conducted some “research” into the origins of the Brett Favre/Hamlet analogy, with entertaining results.

This week on the blog:

I will be posting parts 1(c) and 2 of my Rodman series. The first will examine whether Wilt Chamberlain and Bill Russell were the Gods of Rebounding that Bill Simmons and others always claim they were, and the second will try to pin down exactly how valuable Rodman’s rebounding was to the teams he played for (criticizing PER’s in the process).
I will be posting my Tennis Service Aggression Calculator, which will use a tiny bit of calculus to model whether a player should be more aggressive in their service game.
I will post something on the NFL, either a model for evaluating pre-season predictions that I’ve been working on, or my long-promised “Show Me a Quarterback that Doesn’t Throw Interceptions and I’ll Show You a Sucky Quarterback” analysis.

In the works:

Death, Taxes, and Randy Moss: a discussion of statistical entanglement in the NFL, and the implications for player analysis.
A comprehensive criticism of Hollinger statistics: This will probably be my next big series after the one on Rodman. I hate to do basketball back-to-back, but this research is practically done and dying to be published.
Is Usain Bolt a natural 400 runner?: An examination of the 10m splits for Bolt’s record-setting runs, and what they say about his top speed advantage and his endurance.

By request:

In the comments for Rodman 1(b), Jake asked what the “Ambicourtedness” graph would look like if Rodman were taken out of the sample. This was not difficult, particularly since it looks virtually the same. Here it is:

A friend privately asked me what other NBA stars’ Offensive v. Defensive rebound % graphs looked like, suggesting that, while there may be a tradeoff overall, that doesn’t necessarily mean that the particular lack of tradeoff that Rodman shows is rare. This is a very good question, so I looked at similar graphs for virtually every player who had 5 or more seasons in the “Ambicourtedness Top 1000.” There are other players who have positively sloping trend-lines, though none that come close to Rodman’s. I put together a quick graph to compare Rodman to a number of other big name players who were either great rebounders (e.g., Moses Malone), perceived-great rebounders (e.g., Karl Malone, Dwight Howard), or Charles Barkley:

If you have requests or questions that you would like me to answer on the blog, let me know. And it doesn’t have to be a follow-up to a post I’ve already made: If you have some completely different topic that you would like to see analyzed, or some article that you would like to see reviewed, let me know and I will try to get to it. I can promise that if I get any topic requests that meet the minimal interestingness threshold (that is, I think “hmm, interesting”), I will address at least one of them every week or so.

The Case for Dennis Rodman, Part 1/4 (b)—Defying the Laws of Nature

In this post I will be continuing my analysis of just how dominant Dennis Rodman’s rebounding was. Subsequently, section (c) will cover my analysis of Wilt Chamberlain and Bill Russell, and Part 2 of the series will begin the process of evaluating Rodman’s worth overall.

For today’s analysis, I will be examining a particularly remarkable aspect of Rodman’s rebounding: his ability to dominate the boards on both ends of the court. I believe this at least partially gets at a common anti-Rodman argument: that his rebounding statistics should be discounted because he concentrated on rebounding to the exclusion of all else. This position was publicly articulated by Charles Barkley back when they were both still playing, with Charles claiming that he could also get 18+ rebounds every night if he wanted to. Now that may be true, and it’s possible that Rodman would have been an even better player if he had been more well-rounded, but one thing I am fairly certain of is that Barkley could not have gotten as many rebounds as Rodman the same way that Rodman did.

The key point here is that, normally, you can be a great offensive rebounder, or you can be a great defensive rebounder, but it’s very hard to be both. Unless you’re Dennis Rodman:

To prepare the data for this graph, I took the top 1000 rebounding seasons by total rebounding percentage (the gold-standard of rebounding statistics, as discussed in section (a)), and ranked them 1-1000 for both offensive (ORB%) and defensive (DRB%) rates. I then scored each season by the higher (larger number) ranking of the two. E.g., if a particular season scored a 25, that would mean that it ranks in the top 25 all-time for offensive rebounding percentage and in the top 25 all-time for defensive rebounding percentage (I should note that many players who didn’t make the top 1000 seasons overall would still make the top 1000 for one of the two components, so to be specific, these are the top 1000 ORB% and DRB% seasons of the top 1000 TRB% seasons).

This score doesn’t necessarily tell us who the best rebounder was, or even who was the most balanced, but it should tell us who was the strongest in the weakest half of their game (just as you might rank the off-hand of boxers or arm wrestlers). Fortunately, however, Rodman doesn’t leave much room for doubt: his 1994-1995 season is #1 all-time on both sides. He has 5 seasons that are dual top-15, while no other NBA player has even a single season that ranks dual top-30. The graph thus shows how far down you have to go to find any player with n number of seasons at or below that ranking: Rodman has 6 seasons register on the (jokingly titled) “Ambicourtedness” scale before any other player has 1, and 8 seasons before any player has 2 (for the record, Charles Barkley’s best rating is 215).

This outcome is fairly impressive alone, and it tells us that Rodman was amazingly good at both ORB and DRB – and that this is rare — but it doesn’t tell us anything about the relationship between the two. For example, if Rodman just got twice as many rebounds as any normal player, we would expect him to lead lists like this regardless of how he did it. Thus, if you believe the hypothesis that Rodman could have dramatically increased his rebounding performance just by focusing intently on rebounds, this result might not be unexpected to you.

The problem, though, is that there are both competitive and physical limitations to how much someone can really excel at both simultaneously. Not the least of which is that offensive and defensive rebounds literally take place on opposite sides of the floor, and not everyone gets up and set for every possession. Thus, if someone wanted to cheat toward getting more rebounds on the offensive end, it would likely come, at least in some small part, at the expense of rebounds on the defensive end. Similarly, if someone’s playing style favors one, it probably (at least slightly), disfavors the other. Whether or not that particular factor is in play, at the very least you should expect a fairly strong regression to the mean: thus, if a player is excellent at one or the other, you should expect them to be not as good at the other, just as a result of the two not being perfectly correlated. To examine this empirically, I’ve put all 1000 top TRB% seasons on a scatterplot comparing offensive and defensive rebound rates:

Clearly there is a small negative correlation, as evidenced by the negative coefficient in the regression line. Note that technically, this shouldn’t be a linear relationship overall – if we graphed every pair in history from 0,0 to D,R, my graph’s trendline would be parallel to the tangent of that curve as it approaches Dennis Rodman. But what’s even more stunning is the following:

Rodman is in fact not only an outlier, he is such a ridiculously absurd alien-invader outlier that when you take him out of the equation, the equation changes drastically: The negative slope of the regression line nearly doubles in Rodman’s absence. In case you’ve forgotten, let me remind you that Rodman only accounts for 12 data points in this 1000 point sample: If that doesn’t make your jaw drop, I don’t know what will! For whatever reason, Rodman seems to be supernaturally impervious to the trade-off between offensive and defensive rebounding. Indeed, if we look at the same graph with only Rodman’s data points, we see that, for him, there is actually an extremely steep, upward sloping relationship between the two variables:

In layman’s terms, what this means is that Rodman comes in varieties of Good, Better, and Best — which is how we would expect this type of chart to look if there were no trade-off at all. Yet clearly the chart above proves that such a tradeoff exists! Dennis Rodman almost literally defies the laws of nature (or at least the laws of probability).

The ultimate point contra Barkley, et al, is that if Rodman “cheated” toward getting more rebounds all the time, we might expect that his chart would be higher than everyone else’s, but we wouldn’t have any particular reason to expect it to slope in the opposite direction. Now, this is slightly more plausible if he was “cheating” on the offensive side on the floor while maintaining a more balanced game on the defensive side, and there are any number of other logical speculations to be made about how he did it. But to some extent this transcends the normal “shift in degree” v. “shift in kind” paradigm: what we have here is a major shift in degree of a shift in kind, and we don’t have to understand it perfectly to know that it is otherworldly. At the very least, I feel confident in saying that if Charles Barkley or anyone else really believes they could replicate Rodman’s results simply by changing their playing styles, they are extremely naive.

Addendum (4/20/11):

Commenter AudacityOfHoops asks:

I don’t know if this is covered in later post (working my way through the series – excellent so far), or whether you’ll even find the comment since it’s 8 months late, but … did you create that same last chart, but for other players? Intuitively, it seems like individual players could each come in Good/Better/Best models, with positive slopes, but that when combined together the whole data set could have a negative slope.

I actually addressed this in an update post (not in the Rodman series) a while back:

A friend privately asked me what other NBA stars’ Offensive v. Defensive rebound % graphs looked like, suggesting that, while there may be a tradeoff overall, that doesn’t necessarily mean that the particular lack of tradeoff that Rodman shows is rare. This is a very good question, so I looked at similar graphs for virtually every player who had 5 or more seasons in the “Ambicourtedness Top 1000.” There are other players who have positively sloping trend-lines, though none that come close to Rodman’s. I put together a quick graph to compare Rodman to a number of other big name players who were either great rebounders (e.g., Moses Malone), perceived-great rebounders (e.g., Karl Malone, Dwight Howard), or Charles Barkley:

By my accounting, Moses Malone is almost certainly the 2nd-best rebounder of all time, and he does show a healthy dose of “ambicourtedness.” Yet note that the slope of his trendline is .717, meaning the difference between him and Rodman’s 2.346 is almost exactly twice the difference between him and the -.102 league average (1.629 v .819).

Hey, Do You Think Brett Favre is Maybe Like Hamlet?

On a lighter note: Earlier I was thinking about how tired I am of hearing various ESPN commentators complain about Brett Favre’s “Hamlet impression” – though I was just using the term “Hamlet impression” for the rant in my head, no one was actually saying it (at least this time). I quickly realized how completely unoriginal my internal dialogue was being, and after scolding myself for a few moments, I resolved to find the identity of the first person to ever make the Favre/Hamlet comparison.

Lo and behold, the earliest such reference in the history of the internet – that is, according to Google – was none other than Gregg Easterbrook, in this TMQ column from August 27th, 2003:

TMQ loves Brett Favre. This guy could wake up from a knee operation and fire a touchdown pass before yanking out the IV line. It’s going to be a sad day when he cuts the tape off his ankles for the final time. And it’s wonderful that Favre has played his entire (meaningful) career in the same place, honoring sports lore and appeasing the football gods, never demanding a trade to a more glamorous media market.

But even as someone who loves Favre, TMQ thinks his Hamlet act on retirement has worn thin. Favre keeps planting, and then denying, rumors that he is about to hang it up. He calls sportswriters saying he might quit, causing them to write stories about how everyone wants him to stay; then he calls more sportswriters denying that he will quit, causing them to write stories repeating how everyone wants him to stay. Maybe Favre needs to join a publicity-addiction recovery group. The retire/unretire stuff got pretty old with Frank Sinatra and Michael Jordan; it’s getting old with Favre.

Ha!