In this post I briefly discussed regression to the mean in the NFL, as well as the difficulty one can face trying to beat a simple prediction model based on even a single highly probative variable. Indeed, for all the extensive research and cutting-edge analysis they conduct at Football Outsiders, they are seemingly unable to beat “Koko,” which is just about the simplest regression model known to primates. 
Of course, since there’s no way I could out-analyze F.O. myself — especially if I wanted to get any predictions out before tonight’s NFL opener – I decided to let my computer do the work for me: this is what neural networks are all about. In case you’re not familiar, a neural network is a learning algorithm that can be used as a tool to process large quantities of data with many different variables — even if you don’t know which variables are the most important, or how they interact with each other.
The graphic to the right is the end result of several whole minutes of diligent configuration (after a lot of tedious data collection, of course). It uses 60 variables (which are listed under the fold below), though I should note that I didn’t choose them because of their incredible probative value – many are extremely collinear, if not pointless — I mostly just took what was available on the team and league summary pages on Pro Football Reference, and then calculated a few (non-advanced) rate stats and such in Excel.
Now, I don’t want to get too technical, but there are a few things about my methodology that I need to explain. First, predictive models of all types have two main areas of concern: under-fitting and over fitting. Football Outsiders, for example, creates models that “under fit” their predictions. That is to say, however interesting the individual components may be, they’re not very good at predicting what they’re supposed to. Honestly, I’m not sure if F.O. even checks their models against the data, but this is a common problem in sports analytics: the analyst gets so caught up designing their model a priori that they forget to check whether it actually fits the empirical data. On the other hand, to the diligent empirically-driven model-maker, overfitting — which is what happens when your model tries too hard to explain the data — can be just as pernicious. When you complicate your equations or add more and more variables, it gives your model more opportunity to find an “answer” that fits even relatively large data-sets, but which may not be nearly as accurate when applied elsewhere.
For example, to create my model, I used data from the introduction of the Salary Cap in 1994 on. When excluding seasons where a team had no previous or next season to compare to, this left me with a sample of 464 seasons. Even with a sample this large, if you include enough variables you should get good-looking results: a linear regression will appear to make “predictions” that would make any gambler salivate, and a Neural Network will make “predictions” that would make Nostradamus salivate. But when you take those models and try to apply them to new situations, the gambler and Nostradamus may be in for a big disappointment. This is because there’s a good chance your model is “overfit”, meaning it is tailored specifically to explain your dataset rather than to identifying the outside factors that the data-set reveals. Obviously it can be problematic if we simply use the present data to explain the present data. “Model validation” is a process (woefully ignored in typical sports analysis), by which you make sure that your model is capable of predicting data as well as explaining it. One of the simplest such methods is called “split validation.” This involves randomly splitting your sample in half, creating a “practice set” and a “test set,” and then deriving your model from the practice set while applying it to the test set. If “deriving” a model is confusing to you, think of it like this: you are using half of your data to find an explanation for what’s going on and then checking the other half to see if that explanation seems to work. The upside to this is that if your method of model-creating can pass this test reliably, your models should be just as accurate on new data as they are on the data you already have. The downside is that you have to cut your sample size in half, which leads to bigger swings in your results, meaning you have to repeat the process multiple times to be sure that your methodology didn’t just get lucky on one round.
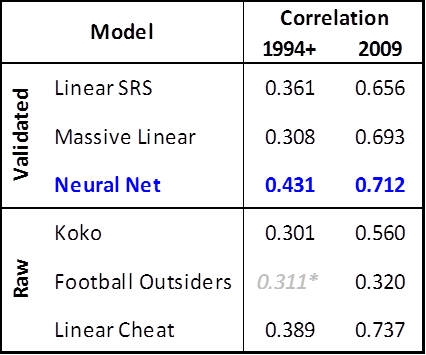
For this model, the main method I am going to use to evaluate predictions is a simple correlation between predicted outcomes and actual outcomes. The dependent variable (or variable I am trying to predict), is the next season’s wins. As a baseline, I created a linear correlation against SRS, or “Simple Rating System,” which is PFR’s term for margin of victory adjusted for strength of schedule. This is the single most probative common statistic when it comes to predicting the next season’s wins, and as I’ve said repeatedly, beating a regression of one highly probative variable can be a lot of work for not much gain. To earn any bragging rights as a model-maker, I think you should be able to beat the linear SRS predictions by at least 5%, since that’s approximately the edge you would need to win money gambling against it in a casino. For further comparison, I also created a “Massive Linear” model, which uses the majority of the variables that go into the neural network (excluding collinear variables and variables that have almost no predictive value). For the ultimate test, I’ve created one model that is a linear regression using only the most probative variables, AND I allowed it to use the whole sample space (that is, I allowed it to cheat and use the same data that it is predicting to build its predictions). For my “simple” neural network, of course, I didn’t do any variable-weighting or analysis myself, and it required very little configuration: I used a very slow ‘learning rate’ (.025 if that means anything to you) with a very high number of learning cycles (5000), with decay on. For the validated models, I repeated this process about 20 times and averaged the outcomes. I have also included the results from running the data through the “Koko” model, and added results from the last 2 years of Football Outsiders predictions. As you will see, the neural network was able to beat the other models fairly handily:
Football Outsider numbers are obviously not since 1994. Note that Koko actually performs on par with F.O. overall, though both are pretty weak compared to the SRS regression or the cheat regression. “Koko” performed very well last season, posting a .560 correlation, though apparently last season was highly “predictable,” as all of the models based on previous patterns performed extremely well. Note also that the Massive Linear model performs poorly: this is as a result of overfitting, as explained above.
Now here is where it gets interesting. When I first envisioned this post, I was planning to title it “Why I Don’t Make Predictions; And: Predictions!” — on the theory that, given the extreme variance in the sport, any highly-accurate model would probably produce incredibly boring results. That is, most teams would end up relatively close to the mean, and the “better” teams would normally just be the better teams from the year before. But when applied the neural network to the data for this season, I was extremely surprised by its apparent boldness:
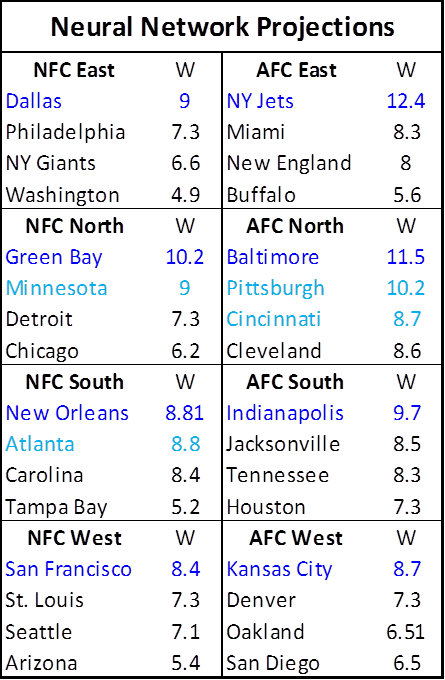
I should note that the numbers will not add up perfectly as far as divisions and conferences go. In fact, I slightly adjusted them proportionally to make them fit the correct number of games for the league as a whole (which should have little or positive effect on its predictive power). SkyNet does not know the rules of football or the structure of the league, and its main goal is to make the most accurate predictions on a team by team basis, and then destroy humanity.
Wait, what? New Orleans struggling to make the playoffs? Oakland with a better record than San Diego? The Jets as the league’s best team? New England is out?!? These are not the predictions of a milquetoast forecaster, so I am pleased to see that my simple creation has gonads. Of course there is obviously a huge amount of variance in this process, and a .43 correlation still leaves a lot to chance. But just to be completely clear, this is exactly the same model that soundly beat Koko, Football Outsiders, and several reasonable linear regressions — some of which were allowed to cheat – over the past 15 years. In my limited experience, neural networks are often capable of beating conventional models even when they produce some bizarre outcomes: For example, one of my early NBA playoff wins-predicting neural networks was able to beat most linear regressions by a similar (though slightly smaller) margin, even though it predicted negative wins for several teams. Anyway, I look forward to seeing how the model does this season. Though, in my heart of hearts, if the Jets win the Super Bowl, I may fear for the future of mankind.
A list of all the input variables, after the jump:
Variables from the previous season (in no particular order):
- Wins
- Losses
- Ties
- Win-Loss Percentage
- Points Allowed
- Point Differential
- Points Fielded
- Made Playoffs
- Strength of Schedule
- Simple Rating System
- Average Margin of Victory
- Offensive Simple Rating System
- Defensive Simple Rating System
- Pass Attempts
- Pass Completions
- Completion percentage
- Passing Yard Differential
- Passing Yards/li>
- Passing Touchdowns
- Passing Touchdown Percentage
- Touchdown to Interception Ratio
- Yards Per Pass Attempt
- Yards Per Completion
- Interceptions
- Interception Percentage
- Percent Passing Plays
- Percent Running Plays
- Rushing Attempts
- Rushing Touchdowns
- Rushing Yardage Differential
- Rushing Yards Per Attempt
- Rushing Yards
- Sacks
- Sack Percentage
- Sack Yards
- Overall Yardage Differential
- Turnover Differential
- Offensive Touchdowns
- Interception Return Touchdowns
- Fumble Recovery Touchdowns
- Defensive Touchdowns
- Kickoff Return Touchdowns
- Punt Return Touchdowns
- Return Touchdowns
- Non-Offensive Touchdowns
- Points Not from Touchdowns.
- Total Touchdowns
- Percentage of Points Coming from Touchdowns
- Coach Stability (number of years coach has been with team prior to the predictor season)
- Quarterback Stability
- Running Back Stability
- Wide Receiver Stability
- New Quarterback?
- 2nd Year Coach?
- 2nd Year Quarterback?
Variables from the offseason (in no particular order):
- New Coach for Predicted Year
- New Quarterback for Predicted Year
- 2nd Year Coach for Predicted Year
- 2nd Year Quarterback for Predicted Year
Out of interest, what did you build your neural network using?
RapidMiner 5