Background: In January, long before I started blogging in earnest, I made several comments on this Advanced NFL Stats post that were critical of Brian Burke’s playoff prediction model, particularly that, with 8 teams left, it predicted that the Dallas Cowboys had about the same chance of winning the Super Bowl as the Jets, Ravens, Vikings, and Cardinals combined. This seemed both implausible on its face and extremely contrary to contract prices, so I was skeptical. In that thread, Burke claimed that his model was “almost perfectly calibrated. Teams given a 0.60 probability to win do win 60% of the time, teams given a 0.70 probability win 70%, etc.” I expressed interest in seeing his calibration data, ”especially for games with considerable favorites, where I think your model overstates the chances of the better team,” but did not get a response.
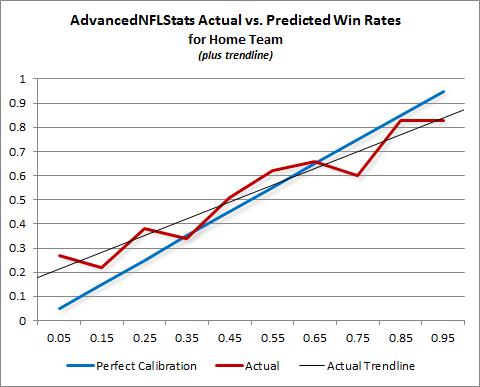
I brought this dispute up in my monstrously-long passion-post, “Applied Epistemology in Politics and the Playoffs,” where I explained how, even if his model was perfectly calibrated, it would still almost certainly be underestimating the chances of the underdogs. But now I see that Burke has finally posted the calibration data (compiled by a reader from 2007 on). It’s a very simple graph, which I’ve recreated here, with a trend-line for his actual data:
Now I know this is only 3+ years of data, but I think I can spot a trend: for games with considerable favorites, his model seems to overstate the chances of the better team. Naturally, Burke immediately acknowledges this error:
On the other hand, there appears to be some trends. the home team is over-favored in mismatches where it is the stronger team and is under-favored in mismatches where it is the weaker team. It’s possible that home field advantage may be even stronger in mismatches than the model estimates.
Wait, what? If the error were strictly based on stronger-than-expected home-field advantage, the red line should be above the blue line, as the home team should win more often than the model projects whether it is a favorite or not – in other words, the actual trend-line would be parallel to the “perfect” line but with a higher intercept. Rather, what we see is a trend-line with what appears to be a slightly higher intercept but a somewhat smaller slope, creating an “X” shape, consistent with the model being least accurate for extreme values. In fact, if you shifted the blue line slightly upward to “shock” for Burke’s hypothesized home-field bias, the “X” shape would be even more perfect: the actual and predicted lines would cross even closer to .50, while diverging symmetrically toward the extremes.
Considering that this error compounds exponentially in a series of playoff games, this data (combined with the still-applicable issue I discussed previously), strongly vindicates my intuition that the market is more trustworthy than Burke’s playoff prediction model, at least when applied to big favorites and big dogs.
You’ve got it backwards. Burke is saying the opposite about home field advantage. You might want to read it again. Burke’s model beats Vegas every year he’s published it. Even 3 years of games divided up in 10 bins would result in the sample errors seen.
No, I didn’t misread him, I quoted him directly: “[T]he home team is over-favored in mismatches where it is the stronger team and is under-favored in mismatches where it is the weaker team” seems correct to me — of course, that is perfectly in line with what I was saying all along. It’s the next sentence: “It’s possible that home field advantage may be even stronger in mismatches than the model estimates” that doesn’t follow from the data (or, strictly speaking, from the sentence before it).
As to whether the game prediction model can beat Vegas overall, I have no strong opinion as I haven’t seen the comparison methodology. I suspect it can beat Vegas slightly, but doubt whether it is by enough to beat the rake. But when its results are wildly divergent from market-based sports predictions — as they are in his playoff model (which I have expressed skepticism towards) — that should give you pause. And, in fact, in my “pause,” I have identified two problems: one is clear-cut and strictly mathematical (see my Epistemology post), and the other was a hypothesis that the model was inaccurate for extreme values. I haven’t yet published an analysis of the model’s methodology, but this data still backs up the hypothesis. Obviously any data with a relatively small sample like this is going to have sample error, so perhaps it is just a coincidence (I would need to see all the data points to do a confidence test), but that doesn’t change the fact that it makes my hypothesis more likely to be true.