The Case for Dennis Rodman, Part 3/4(d)—Endgame: Statistical Significance

The many histograms in sections (a)-(c) of Part 3 reflect fantastic p-values (probability that the outcome occurred by chance) for Dennis Rodman’s win percentage differentials relative to other players, but, technically, this doesn’t say anything about the p-values of each metric in itself. What this means is, while we have confidently established that Rodman’s didn’t just get lucky in putting up better numbers than his peers, we haven’t yet established the extent to which his being one of the best players by this measure actually proves his value. This is probably a minor distinction to all but my most nitpicky readers, but it is exactly one of those nagging “little insignificant details” that ends up being a key to the entire mystery.

The Technical Part (Feel Free to Skip)

The challenge here is this: My preferred method for rating the usefulness and reliability of various statistics is to see how accurate they are at predicting win differentials. But, now, the statistic I would like to test actually is win differential. The problem, of course, is that a player’s win differential is always going to be exactly identical to his win differential. If you’re familiar with the halting problem or Gödel’s incompleteness theorem, you probably know that this probably isn’t directly solvable: that is, I probably can’t design a metric for evaluating metrics that is capable of evaluating itself.

To work around this, our first step must be to independently assess the reliability of win predictions that are based on our inputs. As in sections (b) and (c), we should be able to do this on a team-by-team basis and adapt the results for player-by-player use. Specifically, what we need to know is the error distribution for the outcome-predicting equation—but this raises its own problems.

Normally, to get an error distribution of a predictive model, you just run the model a bunch of times and then measure the predicted results versus the actual results (calculating your average error, standard deviation, correlation, whatever). But, because my regression was to individual games, the error distribution gets “black-boxed” into the single-game win probability.

[A brief tangent: “Black box” is a term I use to refer to situations where the variance of your input elements gets sucked into the win percentage of a single outcome. E.g., in the NFL, when a coach must decide whether to punt or go for it on 4th down late in a game, his decision one way or the other may be described as “cautious” or “risky” or “gambling” or “conservative.” But these descriptions are utterly vapid: with respect to winning, there is no such thing as a play that is more or less “risky” than any other—there are only plays that improve your chances of winning and plays that hurt them. One play may seem like a bigger “gamble,” because there is a larger immediate disparity between its possible outcomes, but a 60% chance of winning is a 60% chance of winning. Whether your chances comes from superficially “risky” plays or superficially “cautious” ones, outside the “black box” of the game, they are equally volatile.]

For our purposes, what this means is that we need to choose something else to predict: specifically, something that will have an accurate and measurable error distribution. Thus, instead of using data from 81 games to predict the probability of winning one game, I decided to use data from 41 season-games to predict a team’s winning percentage in its other 41 games.

To do this, I split every team season since 1986 in half randomly, 10 times each, leading to a dataset of 6000ish randomly-generated half-season pairs. I then ran a logistic regression from each half to the other, using team winning percentage and team margin of victory as the input variables and games won as the output variable. I then measured the distribution of those outcomes, which gives us a baseline standard deviation for our predicted wins metric for a 41 game sample.

Next, as I discussed briefly in section (b), we can adapt the distribution to other sample sizes, so long as everything is distributed normally (which, at every point in the way so far, it has been). This is a feature of the normal distribution: it is easy to predict the error distribution of larger and smaller datasets—your standard deviation will be directly proportional to the square-root of the ratio of the new sample size to the original sample size.

Since I measured the original standard deviations in games, I converted each player’s “Qualifying Minutes” into “Qualifying Games” by dividing by 36. So the sample-size-adjusted standard deviation is calculated like this:

=[41GmStDev]*SQRT([PlQualGames]/41)

Since the metrics we’re testing are all in percentages, we then divide the new standard deviation by the size of the sample, like so:

=([41GmStDev]*SQRT([PlQualGames]/41))/[PlQualGames]

This gives us a standard deviation for actual vs. predicted winning percentages for any sample size. Whew!

The Good, Better, and Best Part

The good news is: now that we can generate standard deviations for each player’s win differentials, this allows us to calculate p-values for each metric, which allows us to finally address the big questions head on: How likely is it that this player’s performance was due to chance? Or, put another way: How much evidence is there that this player had a significant impact on winning?

The better news is: since our standard deviations are adjusted for sample size, we can greatly increase the size of the comparison pool, because players with smaller samples are “punished” accordingly. Thus, I dropped the 3-season requirement and the total minutes requirement entirely. The only remaining filters are that the player missed at least 15 games for each season in which a differential is computed, and that the player averaged at least 15 minutes per game played in those seasons. The new dataset now includes 1539 players.

Normally I don’t weight individual qualifying seasons when computing career differentials for qualifying players, because the weights are an evidentiary matter rather than an impact matter: when it comes to estimating a player’s impact, conceptually I think a player’s effect on team performance should be averaged across circumstances equally. But this comparison isn’t about whose stats indicate the most skill, but whose stats make for the best evidence of positive contribution. Thus, I’ve weighted each season (by the smaller of games missed or played) before making the relevant calculations.

So without further ado, here are Dennis Rodman’s statistical significance scores for the 4 versions of Win % differential, as well as where he ranks against the other players in our comparison pool:

Note: I’ve posted a complete table of z scores and p values for all 1539 players on the site. Note also that due to the weighting, some of the individual differential stats will be slightly different from their previous values.

You should be careful to understand the difference between this table of p-values and ranks vs. similar ones from earlier sections. In those tables, the p-value was determined by Rodman’s relative position in the pool, so the p-value and rank basically represented the same thing. In this case, the p-value is based on the expected error in the results. Specifically, they are the answer to the question “If Dennis Rodman actually had zero impact, how likely would it be for him to have posted these differentials over a sample of this size?” The “rank” is then where his answer ranks among the answers to the same question for the other 1538 players. Depending on your favorite flavor of win differential, Rodman ranks anywhere from 1st to 8th. His average rank among those is 3.5, which is 2nd only to Shaquille O’Neal (whose differentials are smaller but whose sample is much larger).

Of course, my preference is for the combined/adjusted stat. So here is my final histogram:

^{Note: N=1539.}

Now, to be completely clear, as I addressed in Part 3(a) and 2(b), so that I don’t get flamed (or stabbed, poisoned, shot, beaten, shot again, mutilated, drowned, and burned—metaphorically): Yes, actually I AM saying that, when it comes to empirical evidence based on win differentials, Rodman IS superior to Michael Jordan. This doesn’t mean he was the better player: for that, we can speculate, watch the tape, or analyze other sources of statistical evidence all day long. But for this source of information, in the final reckoning, win differentials provide more evidence of Dennis Rodman’s value than they do of Michael Jordan’s.

The best news is: That’s it. This is game, set, and match. If the 5 championships, the ridiculous rebounding stats, the deconstructed margin of victory, etc., aren’t enough to convince you, this should be: Looking at Win% and MOV differentials over the past 25 years, when we examine which players have the strongest, most reliable evidence that they were substantial contributors to their teams’ ability to win more basketball games, Dennis Rodman is among the tiny handful of players at the very very top.

The Case for Dennis Rodman, Part 3/4(c)—Beyond Margin of Victory

In the conventional wisdom, winning is probably overrated. The problem ultimately boils down to information quality: You only get one win or loss per game, so in the short-run, great teams, mediocre team, or teams that just get lucky can all achieve the same results. Margin of victory, on the other hand, has a whole range of possible outcomes that, while imperfectly descriptive of the bottom line, correlate strongly with team strength. You can think about it like sample size: a team’s margin of victory over a handful of games gives you a lot more data to work with than their won-loss record. Thus, particularly when the number of games you draw your data from is small, MOV tends to be more probative.

Long ago, the analytic community recognized this fact, and has moved en masse to MOV (and its ilk) as the main element in their predictive statistics. John Hollinger, for example, uses margin exclusively in his team power ratings—completely ignoring winning percentage—and these ratings are subsequently used for his playoff prediction odds, etc. Note, Hollinger’s model has a lot of baffling components, like heavily weighting a team’s performance in their last 10 games (or later in their last 25% of games), when there is no statistical evidence that L10 is any more predictive than first 10 (or any other 10). But this particular choice is of particular interest, especially as it is indicative of an almost uniform tendency among analysts to substitute MOV-style stats for winning percentage entirely.

This is both logically and empirically a mistake. As your sample size grows, winning percentage becomes more and more valuable. The reason for this is simple: Winning percentage is perfectly accurate—that is, it perfectly reflects what it is that we want to know—but has extremely high variance, while MOV is an imperfect proxy, whose usefulness stems primarily from its much lower variance. As sample sizes increase, the variance for MOV decreases towards 0 (which happens relatively quickly), but the gap between what it measures and what we want to know will persist in perpetuity. Thus, after a certain point, the “error” in MOV remains effectively constant, while the “error” in winning percentage continuously decreases. To get a simple intuitive sense of this, imagine the extremes: after 5 games, clearly you will have more faith in a team that has won 2 but has a MOV of +10 over a team that has won 3 but has a MOV of +1. But now imagine 1000 games with the same MOV’s and winning percentages: one team has won 400 and the other has won 600. If you had to place money on one of the two teams to win their next game, you would be a fool to favor the first. But beyond the intuitive point, this is essentially an empirical matter: with sufficient data, we should be able to establish the relative importance of each for any given sample-size.

So for this post, I’ve employed the same method that I used in section (b) to create our MOV-> Win% formula (logistic regression for all 55,000+ team games since 1986), except this time I included both Win % and MOV (over the team’s other 81 games) as the predictive variables. Here, first, are the coefficients and corresponding p-values (probability that the variable is not significant):

It is thus empirically incontrovertible that, even with an 81-game predictive sample, both MOV and Win% are statistically significant predictive factors. Also, for those who don’t eat logistic regression outputs for breakfast, I should be perfectly clear what this means: It doesn’t just mean that both W% and MOV are good at predicting W%—this is trivially true—it means that, even when you have one, using the other as well will make your predictions substantially better. To be specific, here is the formula that you would use to predict a team’s winning percentage based on these two variables:

$\large{PredictedWin\% = \dfrac{1}{1+e^{-(1.43wp+.081mv-.721)}}}$

Note: Again, e is euler’s number, or ~2.72. wp is the variable for winning % over the other 81 games, and mv is the variable for Margin of Victory over the other 81 games.

And again, for your home-viewing enjoyment, here is the corresponding Excel formula:

=1/(1+EXP(-(1.43*[W%]+.081[MOV]-.721)))

Finally, in order to visualize the relative importance of each variable, we can look at their standardized coefficients (shown here with 95% confidence bars):

^{Note: Standardized coefficients, again, are basically a unit of measurement for comparing the importance of things that come in different shapes and sizes.}

For an 81-game sample (which is about as large of a consistent sample as you can get in the NBA), Win% is about 60% as important as MOV when it comes to predicting outcomes. At the risk of sounding redundant, I need to make this extremely clear again: this does NOT mean that Win% is 60% as good at predicting outcomes as margin of victory (actually, it’s more like 98% as good at that)—it means that, when making your ideal prediction, which incorporates both variables, Win % gets 60% as much weight as MOV (as an aside, I should also note that the importance of MOV drops virtually to zero when it comes to predicting playoff outcomes, largely—though not entirely—because of home court advantage).

This may not sound like much, but I think it’s a pretty significant result: At the end of the day, this proves that there IS a skill to winning games independent of the rates at which you score and allow points. This is a non-obvious outcome that is almost entirely dismissed by the analytical community. If NBA games were a random walk based on possession-to-possession reciprocal advantages, this would not be the case at all.

Now, note that this is formally the same as the scenario discussed in section (b): We want to predict winning percentages, but using MOV alone leaves a certain amount of error. What this regression proves is that this error can be reduced by incorporating win percentage into our predictions as well. So consider this proof-positive that X-factors are predictively valuable. Since the predictive power of Win% and MOV should be equivalent no matter their source, we can now use this regression to make more accurate predictions about each player’s true impact.

Adapting this equation for individual player use is simple enough, though slightly different from before: Before entering the player’s Win% differential, we have to convert it into a raw win percentage, by adding .5. So, for example, if a player’s W% differential were 21.6%, we would enter 71.6%. Then, when a number comes out the other side, we can convert it back into a predicted differential by subtracting .5, etc.

Using this method, Rodman’s predicted win differential comes out to 14.8%. Here is the new histogram:

^{Note: N is still 470.}

This histogram is also weighted by the sample size for each player (meaning that a player with 100 games worth of qualifying minutes counts as 100 identical examples in a much larger dataset, etc.). I did this to get the most accurate distribution numbers to compute P values (which, in this case, work much like a percentile) for individual players. Here is a summary of the major factors for Dennis Rodman:

For comparison, I’ve also listed the percentage of eligible players that match the qualifying thresholds of my dataset (minus the games missed) who are in the Hall of Fame. Specifically, that is, those players who retired in 2004 or earlier and who have at least 3 seasons since 1986 with at least 15 games played in which they averaged at least 15 minutes per game. This gives us a list of 462 players, of which 23 are presently IN the Hall. The difference in average skill between that set of players and the differential set is minimal, and the reddish box on the histogram above surrounds the top 5% of predicted Win% differentials in our main data.

While we’re at it, let’s check in on the list of “select” players we first saw in section (a) and how they rank in this metric, as well as in some of the others I’ve discussed:

For fun, I’ve put average rank and rank of ranks (for raw W% diff, adjusted W% diff, MOV-based regression, raw W%/MOV-based regression, raw X-Factor, adjusted X-Factor, and adjusted W%/MOV-based regression) on the far right. I’ve also uploaded the complete win differential table for all 470 players to the site, including all of the actual values for these metrics and more. No matter which flavor of metric you prefer (and I believe the highlighted one to be the best), Rodman is solidly in Hall of Fame territory.

Finally, I’m not saying that the Hall of Fame does or must pick players based on their ability to contribute to their team’s winning percentages. But if they did, and if these numbers were accurate, Rodman would deserve a position with room to spare. Thus, naturally, one burning question remains: how much can we trust these numbers (and Dennis Rodman’s in particular)? This is what I will address in section (d) tomorrow.

The Case for Dennis Rodman, Part 3/4(b)—Rodman’s X-Factor

The sports analytical community has long used Margin of Victory or similar metrics as their core component for predicting future outcomes. In situations with relatively small samples, it generally slightly outperforms win percentages, even when predicting win percentages.

There are several different methods for converting MOV into expected win-rates. For this series, I took the 55,000+ regular-season team games played since 1986 and compared their outcomes to the team’s Margin of Victory over the other 81 games of the season. I then ran this data through a logistic regression (a method for predicting things that come in percentages) with MOV as the predictor variable. Here is the resulting formula:

$\large{PredictedWin\% = \dfrac{1}{1+e^{-(.127mv-.004}}}$

^{Note: e is euler’s number, or ~2.72. mv is the variable for margin of victory.}

This will return the probability between 0 and 1, corresponding to the odds of winning the predicted game. If you want to try it out for yourself, the excel formula is:

1 / (1 + EXP(-(-0.0039+0.1272*[MOV])))

So, for example, if a team’s point differential (MOV) over 81 games is 3.78 points per game, their odds of winning their 82nd game would be 61.7%.

Of course, we can use this same formula to predict a player’s win% differential based on his MOV differential. If, based on his MOV contribution alone, a player’s team would be expected to win 61.7% of the time, then his predicted win% differential is what his contribution would be above average, in this case 11.7% (this is one reason why, for comparison purposes, I prefer to use adjusted win differentials, as discussed in Part 3(a)).

As discussed in the part 2(b) of this series (“With or Without Worm”), Dennis Rodman’s MOV differential was 3.78 points, which was tops among players with at least a season’s worth of qualifying data, corresponding to the aforementioned win differential of 11.7%. Yet this under-predicts his actual win percentage differential by 9.9%. This could be the result of a miscalibrated prediction formula, but as you can see in the following histogram, the mean for win differential minus predicted win differential for our 470 qualifying player dataset is actually slightly below zero at –0.7%:

Rodman has the 2nd highest overall, which is even more crazy considering that he had one of the highest MOV’s (and the highest of anyone with anywhere close to his sample size) to begin with. Note how much of an outlier he is in this scatterplot (red dot is Rodman):

I call this difference the “X-Factor.” For my purposes, “X” stands for “unknown”: That is, it is the amount of a player’s win differential that isn’t explained by the most common method for predicting win percentages. For any particular player, it may represent an actual skill for winning above and beyond a player’s ability to contribute to his team’s margin of victory (in section (c), I will go about proving that such a skill exists), or it may simply be a result of normal variance. But considering that Rodman’s sample size is significantly larger than the average in our dataset, the chances of it being “error” should be much smaller. Consider the following:

Again, Rodman is a significant outlier: no one with more than 2500 qualifying minutes breaks 7.5%. Rodman’s combination of large sample with large Margin of Victory differential with large X-Factor is remarkable. To visualize this, I’ve put together a 3-D scatter plot of all 3 variables:

It can be hard to see where a point stands in space in a 2-D image, but I’ve added a surface grid to try to help guide you: the red point on top of the red mountain is Dennis Rodman.

To get a useful measure of how extreme this is, we can approximate a sample-size adjustment by comparing the number of qualifying minutes for each player to the average for the dataset, and then adjusting the standard deviation for that player accordingly (proportional to the square root of the ratio, a method which I’ll discuss in more detail in section (d)). After doing this, I can re-make the same histogram as above with the sample-adjusted numbers:

No man is an island. Except, apparently, for Dennis Rodman. Note that he is about 4 standard deviations above the mean (and observe how the normal distribution line has actually blended with the axis below his data point).

Naturally, of course, this raises the question:

Where does Rodman’s X-Factor come from?

Strictly speaking, what I’m calling “X-Factor” is just the prediction error of this model with respect to players. Some of that error is random and some of it is systematic. In section (c), I will prove that it’s not entirely random, though where it comes from for any individual player, I can only speculate.

Margin of Victory treats all contributions to a game’s point spread equally, whether they came at the tail end of a blowout, or in the final seconds of squeaker. One thing that could contribute to a high X-factor is “clutch”ness. A “clutch” shooter (like a Robert Horry), for example, might be an average or even slightly below-average player for most of the time he is on the floor, but an extremely valuable one near the end of games that could go either way. The net effect from the non-close games would be small for both metrics, but the effect of winning close games would be much higher on Win% than MOV. Of course, “clutch”ness doesn’t have to be limited to shooters: e.g., if one of a particular player’s skill advantages over the competition is that he makes better tactical decisions near the end of close games (like knowing when to intentionally foul, etc.), that would reflect much more strongly in his W% than in his MOV.

Also, a player who contributes significantly whenever they are on the floor but is frequently taken out of non-close games as a precaution again fatigue or injury may have a Win % that accurately reflects his impact, but a significantly understated MOV. E.g., in the Boston Celtics “Big 3” championship season, Kevin Garnett was rested constantly—a fact that probably killed his chances of being that season’s MVP—yet the Celtics won by far the most games in the league. In this case, the player is “clutch” just by virtue of being on the floor more in clutch spots.

The converse possibility also exists: A player could be “reverse clutch,” meaning that he plays worse when the game is NOT on the line. This would ultimately have the same statistical effect as if he played better in crunch time. And indeed, based on completely non-rigorous and anecdotal speculation, I think this is a possible factor in Rodman’s case. During his time in Chicago, I definitely recall him doing a number of silly things in the 4th quarter of blowout games (like launching up ridiculous 3-pointers) when it didn’t matter—and in a game of small margins, these things add up.

Finally, though it cuts a small amount against the absurdity of Rodman’s rebounding statistics, I would be derelict as an analyst not to mention the possibility that Rodman may have played sub-optimally in non-close games in order to pad his rebounding numbers. The net effect, of course, would be that his rebounding statistics could be slightly overstated, while his value (which is already quite prodigious) could be substantially understated. To be completely honest, with his rebounding percentages and his X-Factor both being such extreme outliers, I have to think that at least some relationship existing between the two is likely.

If you’re emotionally attached to the freak-alien-rebounder hypothesis, this might seem to be a bad result for you. But if you’re interested in Rodman’s true value to the teams he played for, you should understand that, if this theory is accurate, it could put Rodman’s true impact on winning into the stratosphere. That is, this possibility gives no fuel to Rodman’s potential critics: the worst cases on either side of the spectrum are that Rodman was the sickest rebounder with a great impact on his teams, or that he was a great rebounder with the sickest impact.

In the next section, I will be examining the relative reliability and importance of Margin of Victory vs. Win % generally, across the entire league. In my “endgame” analysis, this is the balance of factors that I will use. But the league patterns do not necessarily apply in all situations: In some cases, a player’s X-factor may be all luck, in some cases it may be all skill, and in most it is probably a mixture of both. So, for example, if my speculation about Rodman’s X-Factor were true, my final analysis of Rodman’s value could be greatly understated.

The Case for Dennis Rodman, Part 3/4(a)—Just Win, Baby (in Histograms)

First off, congratulations to Dennis for making the Hall of Fame finalist list for 2011. The circumstances seem favorable to his making it, and if I had to guess I’d say he probably will. While his under-appreciated status has been a useful vehicle for my analytical agenda, I certainly hope he will be voted in—though I might prefer it be with a copy of my series in the voters’ hands.

Second, I apologize for the delay in getting this section out. I’m reminded of the words of the always brilliant Detective Columbo:

I worry. I mean, little things bother me. I’m a worrier. I mean, little insignificant details – I lose my appetite. I can’t eat. My wife, she says to me, “You know, you can really be a pain.”

Of course, as Columbo understood, the “insignificant” details that nag at you are usually anything but. Since Part 3 of this series should be the last to include heavily-quantitative analysis—and because it is so important to understanding Rodman’s true value—I really tried to tie up all the loose ends (even those that might at first seem to be redundant or obvious).

As a result, what began as a simple observation grew into something painfully detailed and extremely long (even by my standards)—but well worth it. So, once again, I’ve decided to break it down into 4 sections—however, each of these will be relatively short, and I’ll be posting them back-to-back each morning from now through Saturday. Here is the Cliff’s Notes version:

Rodman had an observably great impact on his teams’ winning percentages.
This impact was much greater than his already great impact on Margin of Victory would have predicted.
Contrary to certain wisdom in the analytical community, Margin of Victory and Win% are both valuable indicators predictively, and combining Rodman’s differentials in both put him deep in Hall of Fame territory.
Rodman’s differentials are statistically significant at one of the highest levels in NBA history.

Now, on with the show:

Introduction

One of the most common doubts I hear about Dennis Rodman’s value stems from the belief that his personal successes—5 NBA championships, freakish rebounding statistics, etc.—were probably largely a result of his having played for superior teams. For example, his prodigious rebounding may have been something he was “allowed” to do because he played for good offensive teams and (as the argument goes) had few other offensive responsibilities.

In it’s weaker form, I think this argument is plausible but irrelevant: Perhaps Rodman would not have been able to put up the numbers that he did if he were “required” to do more on offense. But the implication that this diminishes his value is absurd—it would be like saying that Cy Young wasn’t a particularly valuable baseball player because he couldn’t have put up such a great ERA if he were “required” to hit every night.

The stronger form, however, suggests that Rodman’s anomalous rebounding statistics probably weren’t due to any particularly anomalous talent or contribution, but were merely (or at least mostly) a byproduct of his fortunate circumstances.

If this were true, however, one of the following things would necessarily have to follow:

His rebounding must not have contributed much value to his teams, or
The situations he played in must have been uniquely favorable to leveraging value from a designated rebounder, or
The choice to use a designated rebounder on an offensively strong team must have been an extremely successful exploitative strategy.

The third, I technically cannot disprove: It is theoretically possible that Rodman’s refusal to take a lot of shots on offense unintentionally caused his teams to stumble upon an amazing exploitative strategy that no one had discovered before and that no-one has duplicated since (though, if that were the case, he still might deserve some credit for forcing their hands).

But 1 and 2 simply aren’t supported by the data: As I will show, Rodman had wildly positive impacts on 4 different teams that had little in common, except of course for being solid winners with Rodman in the lineup.

Rodman’s Win % Differential

As I’ve discussed previously, a player’s differential statistics are simply the difference in their team’s performance in the games they played versus the games they missed. One very important differential stat we might be interested in is winning percentage.
To look at Rodman’s numbers in this area, I used exactly the same process that I described in Part 2(b) to look at his other differentials. However, for comparison purposes, I’ve greatly expanded the pool of players by dropping the qualifying minutes requirement from 3000 to 1000. This grows the pool from 164 players to 470.

Why expand? Honestly, because Rodman’s extreme win % differential allows it. I think the more stringent filters produce a list that is more reliable from top to bottom—but in this case, I am mostly interested in (literally) the top. There are some players on the list with barely 1/3 of a season’s worth of qualifying playing time to back up their numbers—which should produce extreme volatility—yet still no one is able to overtake Rodman.

Here is Rodman’s raw win differential, along with those of a number of select players (including a few whose styles are often compared to Rodman’s, some Hall of Famers, some future first-ballot Hall of Fame selections, and Rodman’s 2011 Hall of Fame co-finalists Chris Mullin and Maurice Cheeks):

I will put up a table of the entire list of 470 players—including win differentials and a number of other metrics that I will discuss throughout the rest of Part 3—along with section (c) on Friday.
Amazingly, this number may not even reflect Rodman’s true impact, because he generally played for extremely good teams, where it is not only harder to contribute, but where a given impact will have less of an effect on win percentage (for example, if your team normally wins 90% of its games, it is clearly impossible to have a win% differential above 10%). To account for this, I’ve also created “adjusted” win% differentials, which attempt to normalize a player’s percentage increase/decrease to what it would be on a .500 team.

This adjustment is done somewhat crudely, by measuring how far the player gets you toward 100% (for positive impacts) or toward 0% (for negative). E.g., if someone plays for a team that normally wins 70%, and they win 85% with him in the lineup, that is 50% of the way to 100%. Thus, as 50% of the way from 50% to 100% is 75%, that player’s adjusted differential is 25% (as opposed to their raw value of 15%).
A few notes about this method: While I prefer the adjusted numbers for this situation, they have their drawbacks. They are most accurate when dealing with consistently good or bad teams, over multiple seasons, and with bigger sample sizes. They are less accurate with smaller sample sizes, in individual seasons, and with uncertain team quality. This is because regression to the mean can become an interfering factor. When looking at individual seasons in a void, it is relatively easy to account for both effects, which I do for my league-wide win differential analysis. But when aggregating independent seasons that have a common related element—such as the same team or player—you basically have to pick your poison (of course, there may be some way to deal with this issue that I just don’t know or haven’t thought of yet). I will tend to use the adjusted numbers for this analysis, but though they are slightly more favorable to Rodman, either metric leads to the same bottom line. In any case, the tables I will be posting include both metrics (as well as other options).

Dennis Rodman’s adjusted numbers boost his win differential to 21.6%, widening the margin between him and 2nd place. I know I will be flamed if I don’t add that (just as I noted in part 2(b)) I am not claiming that Rodman was actually the best player in the last 25 years. This is a volatile statistic, and Rodman merely happening to have the best win differential among the group of 470 qualifying players does not mean he was actually the best player overall, or even that he was the best player in the group. That said, we should not dismiss the extremeness of the result either:

I will be using a number of (eerily similar) histograms through the rest of Part 3 as well. If you’re not familiar, histograms are one of the simplest and most useful graphical representations of single-variable data (yet, inexplicably, they aren’t built into Excel): each bar represents the number of data points of the designated value. If the variable is continuous (as it is in this case), each bar is basically a “container” that tells you how many data points fit in between the left and right values of the bar (technically it tells you the “density” of points near the center of the container, but those are effectively the same in most circumstances). Their main purpose is to eyeball how the variable is distributed—in this case, as you can see it is distributed normally.

The red line is an overlay of the normal distribution of the sample, which has a mean of –0.5% and standard deviation of 6.3%. This puts Rodman just over 3.5 standard deviations above the mean, a value that should occur about once in every 4000 instances—and he does this based on a standard deviation that is derived from a pool that includes the statistics of many players that have as little as 1/4th as much relevant data as he has.

Moreover, as I will discuss in section (b) tomorrow, his win % differential is not only extreme relative to the rest of the NBA, it is even extreme relative to himself—and this has important implications in its own right.

UPDATE: 2010 NFL Season Neural Network Projections—In Review

Before the start of the 2010 NFL season, I used a very simple neural network to create this set of last-second projections:

Clearly, some of the predictions worked out better than others. E.g., Kansas City did manage to win their division (which I never would have guessed), but Dallas and San Francisco continued to make mockeries of their past selves. We did come dangerously close to a Jets/Packers Super Bowl, but in the end, SkyNet turned out to be more John Edwards than Nostradamus.

From a prediction-tracking standpoint, the real story of this season was the stunning about-face performance of Football Outsiders, who dominated the regular season basically from start to finish:

^{Note: Average and Median Errors reflect the difference between projected and actual wins. Correlations are between projected and actual win percentages.}

Not only did they almost completely flip the results from 2009, but their stellar 2010 results (combined with the below-average outing of my model) actually pushed their last 3 seasons slightly ahead of the neural network overall. This improvement also puts Koko (.25 * previous season’s wins + 6) far in FO’s rearview, providing further evidence that Koko’s 2009 success was a blip.

If we use each method’s win projections to project the post-season as well, however, things turn out a bit differently. Football Outsiders starts out in a strong position, having correctly picked 4 of 8 division champions and 9 of 12 playoff teams overall (against 2 and 8 for the NN respectively), but their performance worsens as the playoffs unfold:

The neural network correctly placed Green Bay in the Super Bowl and the Jets into the AFC championship game, while FO’s final 4 were Atlanta over Green Bay and Baltimore over Indianapolis.

Moreover, if we use these preseason projections to pick the overall results of the playoffs as they were actually set, the neural network outperforms its rivals by a wide margin:

^{Note: The error measured in this table is between predicted finish and actual finish. The Super Bowl winner finishes in 1st place, the loser in 2nd place, conference championship losers each tie for 3.5th place (average of 3rd and 4th), divisional losers tie for 6.5th (average of 5th, 6th, 7th, and 8th), and wild card round losers tie for 10.5th (average of 9th, 10th, 11th, and 12th).}

This minor victory will give me some satisfaction when I retool the model for next season—after all, this model is still essentially based on a small fraction of the variables used by its competitor, and neural networks generally get better and better with more data. On balance, though, the season clearly goes to Football Outsiders. So credit where it’s due, and congratulations to humankind for putting the computers in their place, at least for one more year.

The Case for Dennis Rodman, Part 2/4 (b)—With or Without Worm

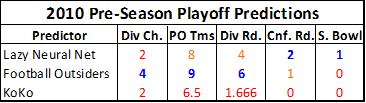
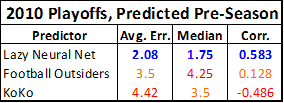
I recently realized that if I don’t speed up my posting of this series, Rodman might actually be in the Hall of Fame before I’m done. Therefore, I’m going to post this section now, and Part 3 (which will probably only be one post) in the next few days.

This blog is called “Skeptical” Sports Analysis for a reason: I’m generally wary of our ability to understand anything definitively, and I believe that most people who confidently claim to know a lot of things other than facts—whether in sports, academics, or life—are either lying, exaggerating, or wrong. I don’t accept this as an a priori philosophical tenet (in college I was actually very resistant to the skeptics), but as an empirical conclusion based on many years of engaging and analyzing various people’s claims of knowledge. As any of you who happen to know me will attest, if I have any talent on this earth, it is finding fault with such claims (even when they are my own).

Keeping that in mind—and keeping in mind that, unlike most sports commentators, I don’t offer broadly conclusive superlatives very often—I offer this broadly conclusive superlative: Dennis Rodman was the greatest rebounder of all time. If there has been any loose end in the arguments I’ve made already, it is this: based on the evidence I’ve presented so far, Rodman’s otherworldly rebounding statistics could, theoretically, be a result of shenanigans. That is, he could simply have been playing at the role of rebounder on his teams, ignoring all else and unnaturally inflating his rebounding stats, while only marginally (or even negatively) contributing to his team’s performance. Thus, the final piece of this puzzle is showing that his rebounding actually helped his teams. If that could be demonstrated, then even my perversely skeptical mind would be satisfied on the point—else there be no hope for knowledge.

This is where “The Case for Dennis Rodman Was a Great Rebounder” and “The Case for Dennis Rodman” join paths: Showing that Rodman got a lot of rebounds without also showing that this significantly improved his teams proves neither that he was a great player nor that he was a great rebounder. Unfortunately, as I discussed in the last two sections, player value can be hard to measure, and the most common conventional and unconventional valuation methods are deeply flawed (not to mention unkind toward Rodman). Thus, in this post and the next, I will take a different approach.

Differential (Indirect) Statistics

For this analysis, I will not be looking at Dennis Rodman’s (or any other player’s) statistics directly at all. Instead, I will be looking at his team’s statistics, comparing the games in which he played to the games that he missed. I used a similar (though simpler) method in my mildly popular Quantum Randy Moss post last fall, which Brian Burke dubbed WOWRM, or “With or Without Randy Moss.” So, now I present that post’s homophonic cousin: WOWWorm, or “With or Without Worm.”

The main advantages to indirect statistics are that they are all-inclusive (everything good or bad that a player does is accounted for, whether it is reflected in the box score or not), empirical (what we do or don’t know about the importance of various factors doesn’t matter), and they can get you about as close as possible in this business to isolating actual cause and effect. These features make the approach especially trenchant for general hypothesis-testing and broader studies of predictivity that include league-wide data.

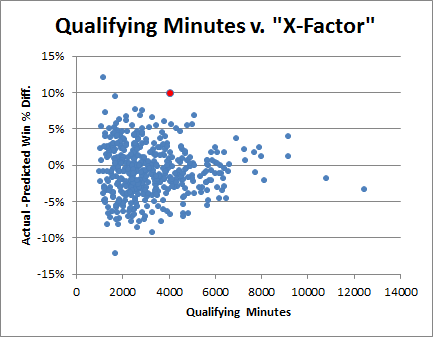
The main disadvantage for individual player analysis, however, is that the samples are almost always too small to be conclusive (in my dream universe, every player would be forced to sit out half of their team’s regular-season games at random). They are also subject to bias based on quality of the player’s team (it is harder to have a big impact on a good team), or based on the quality of their backup—though I think the latter effect is much smaller in the basketball than in football or baseball. In the NBA, teams rotate in many different players and normally have a lot of different looks, so when a starter goes out, they’re rarely just replaced by one person—the whole roster (even the whole gameplan) may shift around to exploit the remaining talent. This is one reason you almost never hear of an NBA bench player finally “getting his shot” because the player in front of them was injured—if someone has exploitable skills, they are probably going to get playing time regardless. Fortunately, Dennis Rodman missed his fair share of games—aided by his proclivity for suspensions—and the five seasons in which he missed at least 15 games came on four different teams.

Note, for the past few years, more complete data has allowed people to look at minute-by-minute or play-by-play +/- in basketball (as has been done for some time in hockey). This basically eliminates the sample size problem, though it introduces a number of potential rotational, strategic and role-based biases. Nevertheless, it definitely makes for a myriad of exciting analytical possibilities.

Margin of Victory

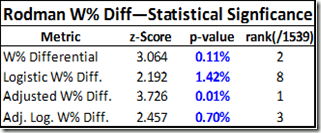
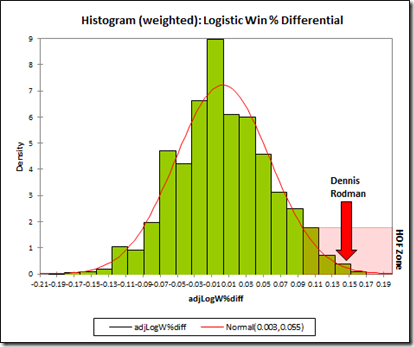
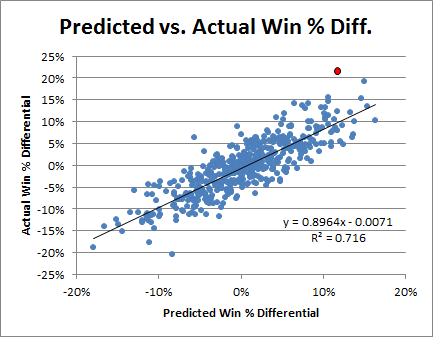
For structural reasons, I’m going to hold off on Rodman’s Win % differentials until my next post in this series. In this post, however, I will look at everything else, starting with team point differential differential—a.k.a. “Margin of Victory”:

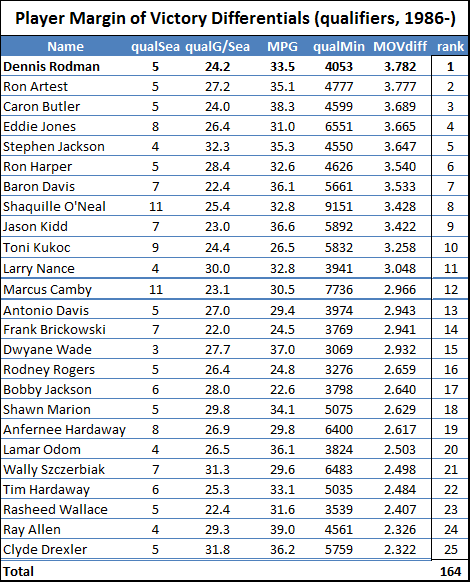
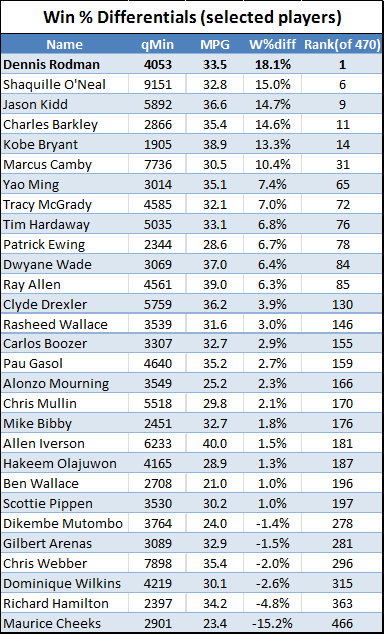
^{Note: Table is only the top 25 players in the dataset.}

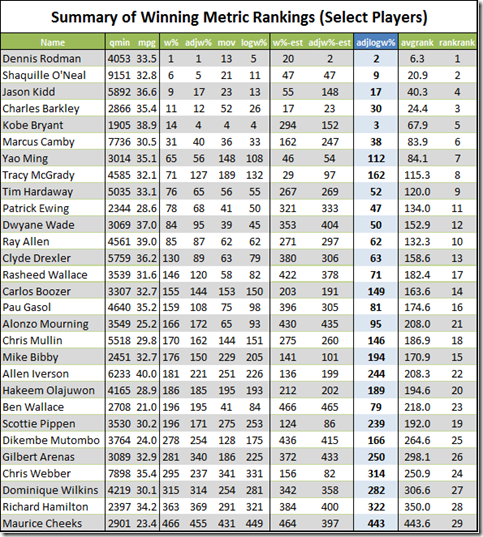
First, the nitty-gritty: This data goes back to 1986, starting with all players who missed and played at least 15 games in a single season while averaging at least 20 minutes per game played. The “qualifying games” in a season is the smaller of games played or games missed. E.g., if someone played 62 games and missed 20, that counts as 20 qualifying games, the same as if someone played 20 games and missed 62. Their “qualifying minutes” are then their average of minutes per game played multiplied by their total number of qualifying games. For the sample, I set the bar at 3000 qualifying minutes, or roughly the equivalent of a full season for a typical starter (82 games * 36 minutes/game is 2952 minutes), which leaves 164 qualifying players. I then calculated differentials for each team-season: I.e., per-game averages were calculated separately for the set of games played and the set of games missed by each player from within a particular season, and each season’s “differentials” were created for each stat simply by subtracting the second from the first. Finally, I averaged the per-season differentials for each qualifying season for each player. This is necessarily different from how multiple-season per-game stats are usually calculated (which is just to sum up the stats from the various seasons and divide by total games). As qualifying games may come from different teams and different circumstances, to isolate a player’s impact it is crucially important that (as much as possible) their presence or absence is the only variable that changes, which is not even remotely possible across multiple seasons. In case anyone is interested, here is the complete table with all differential stats for all 164 qualified players.

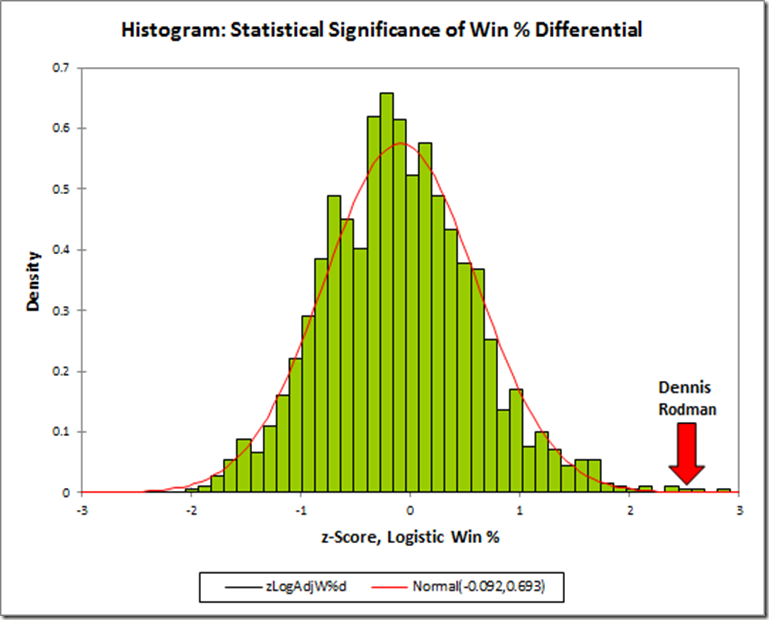
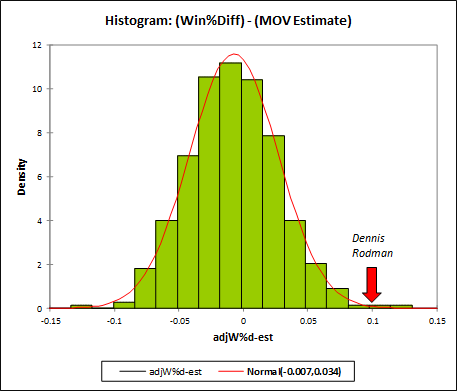
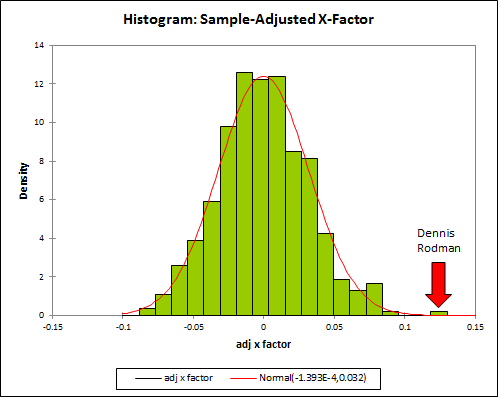
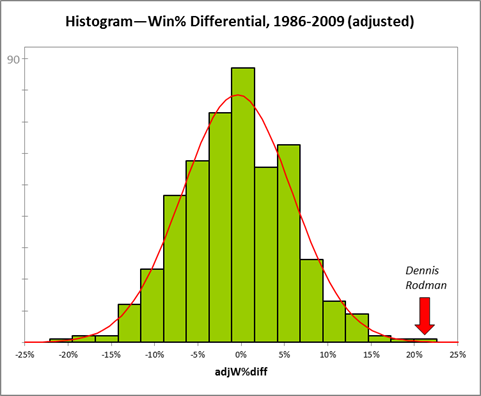
I first ran the differentials for Dennis Rodman quite some time ago, so I knew his numbers were very good. But when I set out to do the same thing for the entire league, I had no idea that Rodman would end up literally on top. Here is a histogram of the MOV-differential distribution for all qualified players (rounded to the nearest .5):

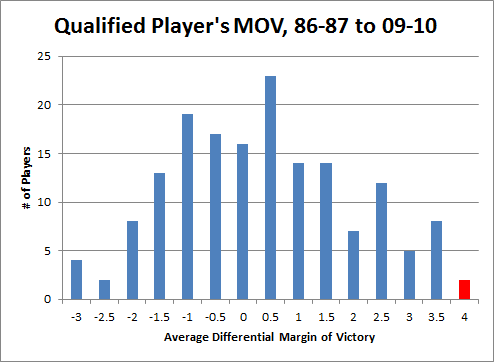
^{Note: Red is Dennis Rodman (and Ron Artest).}

3.8 points per game may not sound like much compared to league-leading scorers who score 30+, but that’s both the beauty of this method and the curse of conventional statistics: When a player’s true impact is actually only a few points difference per night (max), you know that the vast majority of the “production” reflected in their score line doesn’t actually contribute to their team’s margin.

This deserves a little teasing out, as the implications can be non-obvious: If a player who scores 30 points per game is only actually contributing 1 or 2 points to his team’s average margin, that essentially means that at least 28 of those points are either 1) redundant or 2) offset by other deficiencies. With such a low signal-to-noise ratio, you should be able to see how how it is that pervasive metrics like PER can be so unreliable: If a player only scores 10 points a night, but 4 of them are points his team couldn’t have scored otherwise, he could be contributing as much as Shaquille O’Neal. Conversely, someone on the league leaderboard who scores 25 points per game could be gaining his team 2 or 3 points a night with his shooting, but then be giving it all back if he’s also good for a couple of unnecessary turnovers.

Professional basketball is a relatively low-variance sport, but winners are still determined by very small margins. Last year’s championship Lakers team had an average margin of victory of just 4.7 points. For the past 5 years, roughly three quarters of teams have had lower MOV’s than Dennis Rodman’s differential in his 5 qualifying seasons:

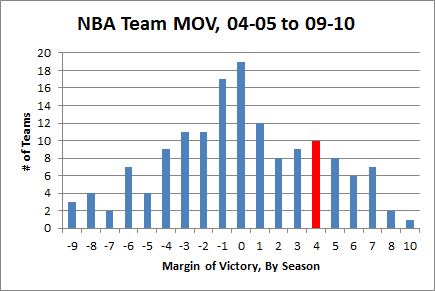
Now, I don’t want to suggest too much with this, but I would be derelict if I didn’t mention the many Hall of Fame-caliber players who qualified for this list below Rodman (my apologies if I missed anyone):

In HoF already:

Hakeem Olajuwon
Scottie Pippen<
Clyde Drexler
Dominique Wilkins

HoF locks:

Shaquille O’Nea
Dwyane Wade
Jason Kidd
Allen Iverson
Ray Allen

HoF possible:

Yao Ming
Pau Gasol
Marcus Camby
Carlos Boozer
Alonzo Mourning

Not in HoF but probably should be:

Toni Kukoc
Chris Mullin
Tim Hardaway
Dikembe Mutumbo

The master list also likely includes many players that are NOT stars but who quietly contributed a lot more to their teams than people realize. Add the fact that Rodman managed to post these differentials while playing mostly for extremely good, contending, teams (where it is harder to have a measurable impact), and was never ostensibly the lynchpin of his team’s strategy—as many players on this list certainly were—and it is really quite an amazing outcome.

Now, I do not mean to suggest that Rodman is actually the most valuable player to lace up sneakers in the past 25 years, or even that he was the most valuable player on this list: 1) It doesn’t prove that, and 2) I don’t think that. Other more direct analysis that I’ve done typically places him “only” in the top 5% or so of starting players. There is a lot of variance in differential statistics, and there are a lot of different stories and circumstances involved for each player. But, at the very least, this should be a wake-up call for those who ignore Rodman for his lack of scoring, and for those who dismiss him as “merely” a role-player.

Where Does His Margin Come From?

As I have discussed previously, one of the main defenses of conventional statistics—particularly vis a vis their failures w/r/t Dennis Rodman—is that they don’t account for defense or “intangibles.” As stated in the Wikipedia entry for PER:

Neither PER nor per-game statistics take into account such intangible elements as competitive drive, leadership, durability, conditioning, hustle, or WIM (wanting it more), largely because there is no real way to quantitatively measure these things.

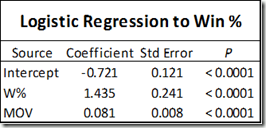
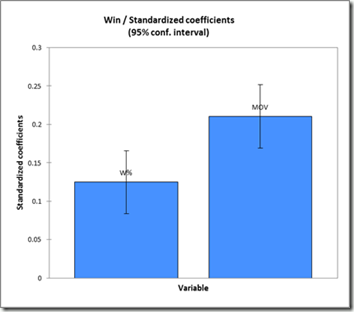
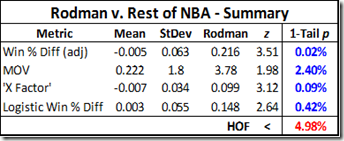
This is true, for the most part—but not so much for Rodman. He does very well with indirect statistics, which actually DO account for all of these things as part of the gestalt that goes into MOV or Win% differentials. But these stats also give us a very detailed picture of where those differences likely come from. Here is a table summarizing a number of Rodman’s differential statistics, both for his teams and their opponents. The “reciprocal advantage” is the difference between his team’s differential and their opponent’s differential for the same statistic:

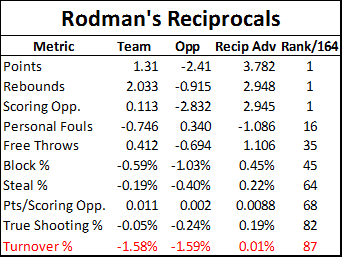
^{Note: Some of the reciprocals were calculated in this table, and others are taken from the dataset (like margin of victory). In the latter case, they may not necessarily match up perfectly, but this is for a number of technical and mathematical reasons that have no significant bearing on the final outcomes.}

Rodman’s Margin of Victory differential comes in part from his teams scoring more points on offense and in part from their allowing fewer points on defense. Superficially, this may look like the majority of Rodman’s impact is coming on the defensive side (-2.4 vs. + 1.3), but that’s deceptive. As you can find in the master table, Rodman also has a significant negative effect on “Pace”—or number of possessions per game—which basically applies equally to both teams. This is almost certainly due to his large number of possession-extending offensive rebounds, especially as he was known (and sometimes criticized) for “kicking it out” and resetting the offense rather than trying to shoot it himself or draw a foul. “Scoring opportunities” are total possessions plus offensive rebounds. As you might expect intuitively, his teams generally had about the same number of these with or without him, because the possessions weren’t actually lost, they were only restarted.

As we can see from the reciprocal table, Rodman had a slightly positive effect on his teams scoring efficiency (points per opportunity), but also had a small positive (though nearly negligible) effect on his opponents’. Thus, combining the effect his rebounding had on number of scoring opportunities with any other effects he had on each side’s scoring efficiency, we can get a fairly accurate anatomy of his overall margin. In case that confused you, here it is broken down step-by-step:

So, roughly speaking, his 3.7ish margin of victory breaks down to roughly 2.8 points from effect on offensive and defensive scoring opportunities and .9 points from the actual value of those opportunities—or, visually:

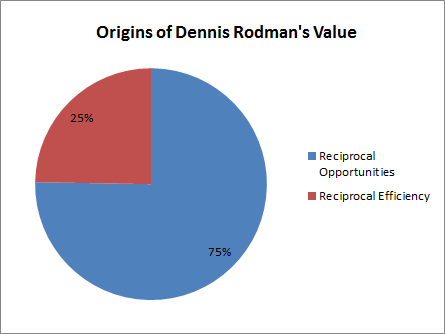
Furthermore, at least part of that extra offensive efficiency likely stems from the fact that a larger proportion of those scoring opportunities began as offensive rebounds, and post-offensive-rebound “possessions” are typically worth slightly more than normal (though this may actually be less true with Rodman due to the “kicking”). Otherwise, the exact source of the efficiency differences is much more uncertain, especially as the smaller margins in the other statistics are that much more unreliable because of the sample-size issues inherent in this method.

The next-strongest reciprocal effects on the list above appear to be personal fouls and their corresponding free throws: with him in the lineup, his teams had fewer fouls and more free throws, and his opponents the opposite. This is particularly peculiar because Rodman himself got a lot of fouls and was a terrible free throw shooter (note: this is yet another reason why including personal fouls in your player valuation method—yes, I’m looking at you, PER—is ridiculous).

Whether Rodman was a “role player” or not is irrelevant: whatever his role, he did it well enough to contribute more to his teams than the vast majority of NBA players (role players or not) contributed to theirs. For some reason, this simple concept seems to be better understood in other sports: No-one would say that Mariano Rivera hasn’t contributed much to the Yankees winning because he is “merely” a closer (though I do think he could contribute more if he pitched more innings), just as no-one would say that Darrelle Revis hasn’t contributed much to the Jets because he is “merely” a cornerback.

So does this mean I am conceding that Rodman was just a very good, but one-dimensional, player? Not that there would be anything wrong with that, but definitely not. That is how I would describe it if he had hurt his team in other areas, but then made up for it—and then some—through excellent rebounding. This is actually probably how most people would predict that Rodman’s differentials would break down (including, initially, myself), but they don’t. E.g., the fact that his presence on the court didn’t hurt his team’s offensive efficiency, despite hardly ever scoring himself, is solid evidence that he was actually an excellent offensive player. Even if you take the direct effects of his rebounds out of the equation entirely, he still seems to have made three different championship contenders—including one of the greatest teams of all time—better. While the majority of his value added—that which enabled him to significantly improve already great teams—came from his ability to grab rebounds that no one else would have gotten, the full realization of that value was made possible by his not hurting those teams significantly in any other way.

As it wasn’t mystical intangibles or conveniently immeasurable defensive ability that made Rodman so valuable, I think it is time we rescind the free pass given to the various player valuation metrics that have relied on that excuse for getting this one so wrong for so long. However, this does not prove that even a perfectly-designed metric would necessarily be able to identify this added value directly. Though I think valuation metrics can be greatly improved (and I’m trying to do so myself), I can’t say for certain that my methods or any others will definitely be able to identify which rebounds actually helped a team get more rebounds and which points actually helped a team score more points. Indeed, a bench player who scores 8 points per game could be incredibly valuable if they were the right 8 points, even if there were no other direct indications (incidentally, this possibility has been supported by separate research I’ve been doing on play-by-play statistics from the last few seasons, in which I’ve found that a number of bench players have contributed much more to their teams than most people would have guessed possible). But rather than throwing our hands in the air and defending inadequate pre-existing approaches, we should be trying to figure out how and whether these sorts of problems can be addressed.

Defensive Stalwart or Offensive Juggernaut?

As an amusing but relevant aside, you may have already noticed that the data—at least superficially—doesn’t even seem to support the conventional wisdom that, aside from his rebounding, Rodman was primarily a defensive player. Most obviously, his own team’s points per scoring opportunity improved, but his opponents’ improved slightly as well. If his impact were primarily felt on the defensive side, we would probably expect the opposite. Breaking down the main components above into their offensive and defensive parts, our value-source pie-chart would look like this.

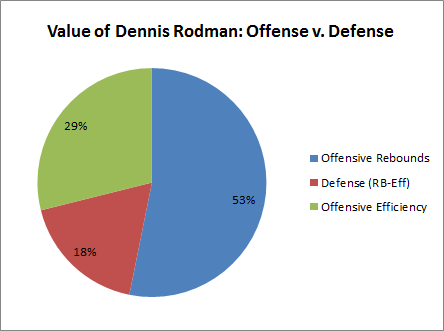
The red is actually slightly smaller than his contribution from defensive rebounds alone, as technically defensive efficiency was slightly lower with Rodman in the games. For fun, I’ve broken this down a bit further into an Offense vs. Defense “Tale of the Tape,” including a few more statistics not seen above:

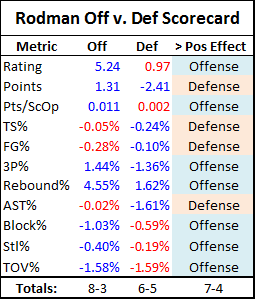
^{Note: Differentials that help their respective side are highlighted in blue, and those that hurt their respective side are highlighted in Red. The values for steals and blocks are each transposed from their team and opponent versions above, as these are defensive statistics to begin with.}

Based on this completely ridiculous and ad-hoc analysis, it would seem that Rodman was more of an offensive player than a defensive one.

Including rebounding, I suspect it is true that Rodman’s overall contribution was greater on offense than defense. However, I wouldn’t read too much into the breakdowns for each side. Rodman’s opponents scoring slightly more per opportunity with him in the game does NOT prove that he was a below-average defender. Basketball is an extremely dynamic game, and the effects of success in one area may easily be realized in others. For example, a strong defensive presence may free up other players to focus on their team’s offense, in which case the statistical consequences could be seen on the opposite side of the floor from where the benefit actually originated.

There are potential hints of this kind of possibility in this data, such as: Why on earth would Rodman’s teams shoot better from behind the arc, considering that he was only a .231 career 3-point shooter himself? This could obviously just be noise, but it’s also possible that some underlying story exists in which more quality long-range shots opened up as a result of Rodman’s successes in other assignments. Ultimately, I don’t think we can draw any conclusions on the issue, but the fact that this is even a debatable question has interesting implications, both for Dennis Rodman and for basketball analytics broadly.

Conclusions

While I am the first to admit that the dataset this analysis is based on might not be sufficiently robust to settle the entire “Case” on its own, I still believe these results are powerful evidence of the truth of my previous inferences—and for very specific reasons:

Assessing the probability of propositions that have a pre-conceived likelihood of being true in light of new evidence can be tricky business. In this case, the story goes like this: I developed a number of highly plausible conclusions about Rodman’s value based on a number of reasonable observations and empirical inquiries, such as: 1) the fact that his rebounding prowess was not just great, but truly extreme, 2) the fact that his teams always seemed to do extremely well on both ends of the floor, and 3) my analysis (conducted for reasons greater than just this series) suggesting that A) scoring is broadly overrated, B) rebounding is broadly underrated, and C) that rebounding has increasing marginal returns (or is exponentially predictive). Then, to further examine these propositions, I employed a completely independent method—having virtually no overlap with the various factors involved in those previous determinations—and it not only appears to confirm my prior beliefs, but does so even more than I imagined it would.

Now, technically, it is possible that Rodman just got extremely lucky in the differential data—in fact, for this sample size, getting that lucky isn’t even a particularly unlikely event, and many of his oddball compatriots near the top of the master list probably did just that. But this situation lends itself perfectly to Bayes’ Theorem-style analysis. That is, which is the better, more likely explanation for this convergence of results: 1) that my carefully reasoned analysis has been completely off-base, AND that Rodman got extremely lucky in this completely independent metric, or 2) that Dennis Rodman actually was an extremely valuable player?