Seriously, I am dying to post about something non-NBA related, and I should have my Open-era tennis ELO ratings by surface out in the next day or so. But last night I finally got around to checking the betting markets to see how the NBA Finals—and thus my chances of winning the Smackdown—were shaping up, and I was shocked by what I found. Anyway, I tossed a few numbers around, and thought you all might find them interesting. Plus, there’s a nice little object-lesson about the usefulness of small sample size information for making Bayesian inferences. This is actually one area where I think the normal stat geek vs. public dichotomy gets turned on its head: Most statistically-oriented people reflexively dismiss any empirical evidence without a giant data-set. But in certain cases—particularly those with a wide range of coherent possibilities—I think the general public may even be a little too conservative about the implications of seemingly minor statistical anomalies.
Freaky Finals Odds:
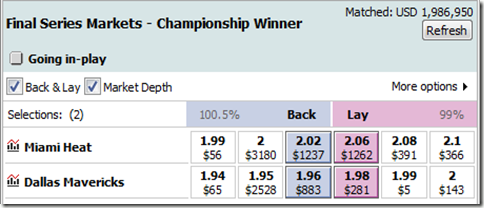
First, I found that most books seem to see the series as a tossup at this point. Here’s an example from a European sports-betting market:
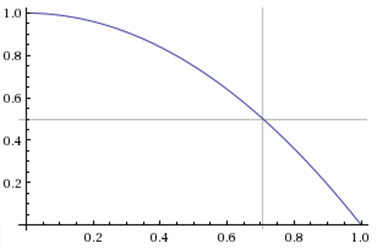
Intuitively, this seemed off to me. Dallas needs to win 1 out of the 2 remaining games in Miami. Assuming the odds for both games are identical (admittedly, this could be a dubious assumption), here’s a plot of Dallas’s chances of winning the series relative to Miami’s expected winrate per home game:
So for the series to be a tossup, Miami needs to be about a 71% favorite per game. Even at home in the playoffs, this is extremely high. Depending on what dataset you use, the home team wins around 60-65% of the time in the NBA regular season and about 65%-70% of the time in the postseason. But that latter number is a bit deceptive, since the playoffs are structured so that more games are played in the homes of the better teams: aside from the 2-3-2 Finals, any series that ends in an odd number of games gives the higher-seeded team (who is often much better) an extra game at home. In fact, while I haven’t looked into the issue, that extra 5% could theoretically be less than the typical skill-disparity between home and away teams in the playoffs, which would actually make home court less advantageous than in the regular season.
Now, Miami has won only 73% of their home games this season, and it was against below-average competition (overall, they had one of the weakest schedules in the league). Counting the playoffs, at this point Dallas actually has a better record than Miami (by one game), and they played an above-average schedule. More importantly, the Mavs won 68% of their games on the road (compare to the league average of 35-40%). Not to mention, Dallas is 5-2 against the Heat overall, and 2-1 against them at home (more on that later).
So how does the market tilt so heavily to this side? Honestly, I have no idea. Many people are much more willing to dismiss seemingly incongruent market outcomes than I am. While I obviously think the market can be beaten, when my analytical results diverge wildly from what the money says, my first inclination is to wonder what I’m doing wrong, as the odds of a massive market failure are probably lower than the odds that I made a mistake. But, in this case, with comparatively few variables, I don’t really get it.
It is a well-known phenomenon in sports-betting that huge games often have the juiciest (i.e., least efficient) lines. This is because the smart money that normally keeps the market somewhat efficient can literally start to run out. But why on earth would there be a massive, irrational rush to bet on the Heat? I thought everyone hated them!
Fun With Meta-Analysis:
So, for amusement’s sake, let’s imagine a few different lines of reasoning (I’ll call them “scenarios”) that might lead us to a range of different conclusions about the present state of the series:
- Miami won at Home ~73% of the time while Dallas won on the road (a fairly stunning) 68% of the time. If these values are taken at face value, a generic Miami Home team would be roughly 5% better than a generic Dallas road team, making Miami a 52.5% favorite in each game.
- The average home team in the NBA wins about 63% of the time. Miami and Dallas seem pretty evenly matched, so Miami should win each game ~63% of the time as well.
- Let’s go with the very generous end of broader statistical models (discounting early-season performance, giving Miami credit for championship experience, best player, and other factors), and assume that Miami is about 5-10% better than Dallas on a neutral site. The exact math on this is complicated (since winning is a logistic function), but, ballpark, this would translate into about a 65.5% chance at home.
- Markets rule! Approximate Market Price for a Miami series win is ~50%, translating into the 71% chance mentioned above above.
Here’s a scatter-plot of the chances of Dallas winning the series based on those per-game estimates:
Ignore the red dots for now—we’ll get back to those. The blue dots are the probability of Dallas winning at least one of the next two games (using the same binomial formula as the function above). Now, hypothetically, let’s assume you thought each of these analyses were equally plausible, your overall probability for Dallas winning the title would simply be the average of the four scenario’s results, or right around 60%. Note: I am NOT endorsing any of these lines of reasoning or any actual conclusions about this series here—it’s just a thought experiment.
A Little Bayesian Inference:
As I mentioned above, the Mavericks are 5-2 against the Heat this season, including 2-1 against them in Miami. Let’s focus on the second stat: Sticking with the assumption that you found each of these 4 lines of reasoning equally plausible prior to knowing Dallas’s record in Miami, how should your newly-acquired knowledge that they were 2-1 affect your assessment?
Well, wow! 3 games is such a miniscule sample, it can’t possibly be relevant, right? I think most people—stat geek and layperson alike—would find this statistical event pretty unremarkable. In the abstract, they’re right: certainly you wouldn’t let such a thing invalidate a method or process built on an entire season’s worth of data. Yet, sometimes these little details can be more important than they seem. Which brings us to perhaps the most ubiquitously useful tool discovered by man since the wheel: Bayes’ Theorem.
Bayes’ Theorem, at it’s heart, is a fairly simple conceptual tool that allows you to do probability backwards: Garden-variety probability involves taking a number of probabilistic variables and using them to calculate the likelihood of a particular result. But sometimes you have the result, and would like to know how it affects the probabilities of your conditions: Bayesian analysis makes this possible.
So, in this case, instead of looking at the games or series directly, we’re going to look at the odds of Dallas pulling off their 2-1 record in Miami under each of our scenarios above, and then use that information to adjust the probabilities of each. I’ll go into the detail in a moment, but the relevant Bayesian concept is that, given a result, the new probability of each precondition will be adjusted proportionally to its prior probability of producing that result. Looking at the red dots above (which are technically the cumulative binomial probability of Miami winning 0 or 1 out of 3 games), you should see that Dallas is far more likely to go 2-1 or better on Miami’s turf if they are an even match than if Miami is a huge favorite—over twice as likely, in fact. Thus, we should expect that scenarios suggesting the former will become much more likely, and scenarios suggesting the latter will become much less so.
In its simplest form, Bayes’ Theorem states that the probability of A given B is equal to the probability of B given A times the prior probability of A (probability before our new information), divided by the prior probability of B:
Though our case looks a little different from this, it is actually a very simple example. First, I’ll treat the belief that the four analyses are equally likely to be correct as a “discrete uniform distribution” of a single variable. That sounds complicated, but it simply means that there are 4 separate options, one of which is actually correct, and each of which is equally likely. Thus, the odds of any given scenario are expressed exactly as above (B is the 2-1 outcome):
The prior probability for Sx is .25. The prior probability of our result (the denominator) is simply the sum of the probabilities of each scenario producing that result, weighted by each scenario’s original probability. But since these are our only options and they are all equal, that element will factor out, as follows:
Since P(Sx) appears in both the numerator and the denominator, it cancels out, leaving our probability for each scenario as follows:
The calculations of P(B|Sx) are the binomial probability of Dallas winning exactly 2 out of 3 games in each case (note this is slightly different from above, so that Dallas is sufficiently punished for not winning all 3), and Excel’s binom.dist() function makes this easy. Plugging those calculations in with everything else, we get the following adjusted probabilities for each scenario:
Note that the most dramatic changes are in our most extreme scenarios, which should make sense both mathematically and intuitively: going 2-1 is much more meaningful if you’re a big dog.
Our new weighted average is about 62%, meaning the 2-1 record improves our estimate of Dallas’s chances by 2%, making the gap between the two 4%: 62-38 (24% difference) instead of 60-40. That may not sound like much, but a few percentage points of edge aren’t that easy to come by. For example, to a gambler, that 4% could be pretty huge: you normally need a 5% edge to beat the house (i.e., you have to win 52.5% of the time), so imagine you were the only person in the world who knew of Dallas’s miniature triumph—in this case, that info alone could get you 80% of the way to profit-land.
Making Use:
I should note that, yes, this analysis makes some massively oversimplifying assumption—in reality, there can be gradients of truths between the various scenarios, with a variety of interactions and hidden variables, etc.—but you’d probably be surprised by how similar the results are whether you do it the more complicated way or not. One of the things that makes Bayesian inference so powerful is that it often reveals trends and effects that are relatively insulated from incidental design decisions. I.e., the results of extremely simplified models are fairly good approximations of those produced by arbitrarily more robust calculations. Consequently, once you get used to it, you will find that you can make quick, accurate, and incredibly useful inferences and estimates in a broad range of practical contexts. The only downside is that, once you get started on this path, it’s a bit like getting Tetrisized: you start seeing Bayesian implications everywhere you look, and you can’t turn it off.
Of course, you also have to be careful: despite the flexibility Bayesian analysis provides, using it in abstract situations—like a meta-analysis of nebulous hypotheses based on very little new information—is very tricky business, requiring good logical instincts, a fair capacity for introspection, and much practice. And I can’t stress enough that this is a very different beast from the typical talking head that uses small samples to invalidate massive amounts of data in support of some bold, eye-catching and usually preposterous pronouncement.
Finally, while I’m not explicitly endorsing any of the actual results of the hypo I presented above, I definitely think there are real-life equivalents where even stronger conclusions can be drawn from similarly thin data. E.g., one situation that I’ve tested both analytically and empirically is when one team pulls off a freakishly unlikely upset in the playoffs: it can significantly improve the chances that they are better than even our most accurate models (all of which have significant error margins) would indicate.