First of all, congrats to Dennis for his well-deserved selection as a 2011 Hall of Fame inductee—of course, I take full credit.  But seriously, when the finalists were announced, I immediately suspected that he would make the cut, mostly for two reasons:

1. Making the finalists this year after failing to make the semi-finalists last year made it more likely that last year’s snub really was more about eligibility concerns than general antipathy or lack of respect toward him as a player.
2. The list of co-finalists was very favorable.  First, Reggie Miller not making the list was a boon, as he could have taken the “best player” spot, and Rodman would have lacked the goodwill to make it as one of the “overdue”—without Reggie, Rodman was clearly the most accomplished name in the field.  Second, Chris Mullen being available to take the “overdue” spot was the proverbial “spoonful of sugar” that allowed the bad medicine of Rodman’s selection go down.

Congrats also to Artis Gilmore and Arvydas Sabonis.  In my historical research, Gilmore’s name has repeatedly popped up as an excellent player, both by conventional measures (11-time All-Star, 1xABA Champion, 1xABA MVP, led league in FG% 7 times), and advanced statistical ones (NBA career leader in True Shooting %, ABA career leader in Win Shares and Win Shares/48, and a great all-around rebounder).  It was actually only a few months ago that I first discovered—to my shock—that he was NOT in the Hall [Note to self: cancel plans for “The Case for Artis Gilmore”].  Sabonis was an excellent international player with a 20+ year career that included leading the U.S.S.R. to an Olympic gold medal and winning 8 European POY awards.  I remember following him closely when he finally came to the NBA, and during his too-brief stint, he was one of the great per-minute contributors in the league (though obviously I’m not a fan of the stat, his PER over his first 5 season—which were from age 31-35—was 21.7, which would place him around 30th in NBA history).  Though his sample size was too small to qualify for my study, his adjusted win percentage differential over his NBA career was a very respectable 9.95%, despite only averaging 24 minutes per game.

I was hesitant to publish Part 4 of this series before knowing whether Rodman made the Hall or not, as obviously the results shape the appropriate scope for my final arguments. So by necessity, this section has changed dramatically from what I initially intended.  But I am glad I waited, as this gives me the opportunity to push the envelope of the analysis a little bit:  Rather than simply wrapping up the argument for Rodman’s Hall-of-Fame candidacy, I’m going to consider some more ambitious ideas.  Specifically, I will articulate two plausible arguments that Rodman may have been even more valuable than my analysis so far has suggested.  The first of these is below, and the second—which is the most ambitious, and possibly the most shocking—will be published Monday morning in the final post of this series.

Introduction

I am aware that I’ve picked up a few readers since joining “the world’s finest quantitative analysts of basketball” in ESPN’s TrueHoop Stat Geek Smackdown.  If you’re new, the main things you need to know about this series are that it’s 1) extremely long (sprawling over 13 sections in 4 parts, plus a Graph of the Day), 2) ridiculously (almost comically) detailed, and 3) only partly about Dennis Rodman.  It’s also a convenient vehicle for me to present some of my original research and criticism about basketball analysis.

Obviously, the series includes a lot of superficially complicated statistics, though if you’re willing to plow through it all, I try to highlight the upshots as much as possible.  But there is a lot going on, so to help new and old readers alike, I have a newly-updated “Rodman Series Guide,” which includes a broken down list of articles, a sampling of some of the most important graphs and visuals, and as of now, a giant new table summarizing the entire series by post, including the main points on both sides of the analysis.  It’s too long to embed here, but it looks kind of like this:

As I’ve said repeatedly, this blog isn’t just called “Skeptical” Sports because the name was available: When it comes to sports analysis—from the mundane to the cutting edge—I’m a skeptic.  People make interesting observations, perform detailed research, and make largely compelling arguments—which is all valuable.  The problems begin when then they start believing too strongly in their results: they defend and “develop” their ideas and positions with an air of certainty far beyond what is objectively, empirically, or logically justified.

With that said, and being completely honest, I think The Case For Dennis Rodman is practically overkill.  As a skeptic, I try to keep my ideas in their proper context: There are plausible hypotheses, speculative ideas, interim explanations requiring additional investigation, claims supported by varying degrees of analytical research, propositions that have been confirmed by multiple independent approaches, and the things I believe so thoroughly that I’m willing to write 13-part series’ to prove them.  That Rodman was a great rebounder, that he was an extremely valuable player, even that he was easily Hall-of-Fame caliber—these propositions all fall into that latter category: they require a certain amount of thoughtful digging, but beyond that they practically prove themselves.

Yet, surely, there must be a whole realm of informed analysis to be done that is probative and compelling but which might fall short of the rigorous standards of “true knowledge.”  As a skeptic, there are very few things I would bet my life on, but as a gambler—even a skeptical one—there are a much greater number of things I would bet my money on.  So as my final act in this production, I’d like to present a couple of interesting arguments for Rodman’s greatness that are both a bit more extreme and a bit more speculative than those that have come before.  Fortunately, I don’t think it makes them any less important, or any less captivating:

Argument 1: Fun With Occam’s Razor

There are two things from my analysis that should be abundantly clear:  1) Dennis Rodman was an great rebounder, and 2) Dennis Rodman had a great impact on winning.  Not only do I feel I’ve proven both of these to be true beyond any doubt, I think I’ve proven them to be even more true than I could have possibly guessed.  Which is to say, Rodman’s rebounding ability and his impact on winning both turned out to be significantly greater than I imagined at the outset.

Yet, however incredible those outcomes may have been, they are far from the most shocking.  Rather, there are two specific discoveries that blew my mind.  They are both important causal elements in my final analysis, but neither has any readily-apparent explanation behind them:

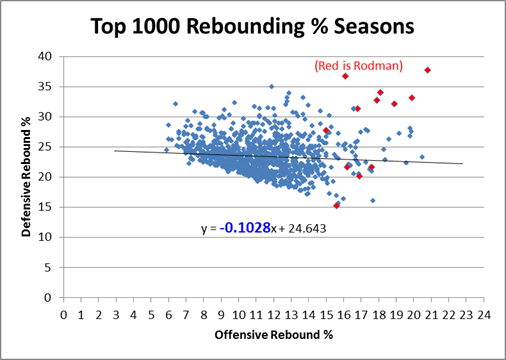
1). The nature-defying lack of tradeoff between Rodman’s offensive and defensive rebounding, as exemplified in this graph from Part 1(b):

The initial post of course, has a more detailed explanation, including a recently-added comparison with some other great rebounders.

And:

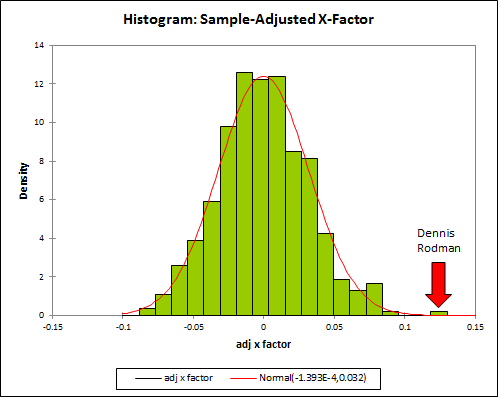
2). The fact that Rodman’s observed win percentage differential is so massively higher than what would be predicted by his already extremely high “Margin of Victory” differential.  After adjusting for sample-size, the extremeness of his “X-Factor” was demonstrated in this histogram from Part 3(b):

And this graph actually doesn’t even account for the fact that extremely high predicted differentials should be far more likely to over-predict rather than under-predict a player’s actual differential.  For those unfamiliar with “regression to the mean,” a quick illustration: Imagine 4 well-known sluggers who hit 25, 35, 45, and 55 homeruns in a particular season—who is most likely to have the largest increase in their HR total the following season?  If you said they guy who hit 55, you are probably one of Barry Bonds’ attorneys.

The Theory:

If you’ve ever watched House, you’re probably aware that a key tenet in diagnostics is: When you see two extremely rare and/or unlikely symptoms in the same patient, even if they seem completely unrelated, they are probably related.  Either one is somehow causing the other, or something else causes both, etc.  This is a medical application of Occam’s razor, which is frequently misstated as a rule that “the simplest explanation is normally the best one.”  There are many permutations of the razor, but here is an earlier and more accurate form:

pluralitas non est ponenda sine necessitate

or

plurality should not be posited without necessity

In practical terms, it means that we should favor the explanation with the fewest number of assumptions.  In the medical case, you can either make two assumptions: 1) that the patient has incredibly rare condition x, and 2) that he has incredibly rare condition y; or one: that there is some condition z that you haven’t thought of yet (incredibly rare or not), from which x and y both follow.

Rodman’s case is no different: We have two incredibly bizarre phenomenon that practically beg for a unifying explanation, or at least an explanation that would make them seem less bizarre.  In Part 3(b), I briefly speculated about such a theory: that Rodman may actually have been “Reverse Clutch”—which is to say, he may have played worse in situations where the game was not on the line.  Specifically, the theory goes, to pad his rebounding statistics, Rodman may have played sub-optimally in meaningless situations by going after extra rebounds.  If he picked his “selfish” spots judiciously—that is, when the outcome of the game really wouldn’t be affected—this would have little to no effect on his Win % differential: he should win the same amount as if he had played optimally throughout.  But, his team’s dominating wins would be slightly less dominant, and their bad losses would be slightly worse, which would have a negative effect on his MOV differential.

Occam’s razor itself can be seen as a special case in the broader realm of Bayesian inference.  But leaving the math and epistemology aside, the practical point is this: An explanation which itself seems like an incredible longshot, may indeed become likely, or even a virtual certainty, if it is the simplest way of explaining other phenomenon.

The Data:

Before getting into the ins and outs of whether this could be a plausible explanation (or at least explanatory factor) for our two freakish anomalies, we should check to see whether the theory is consistent with available data.

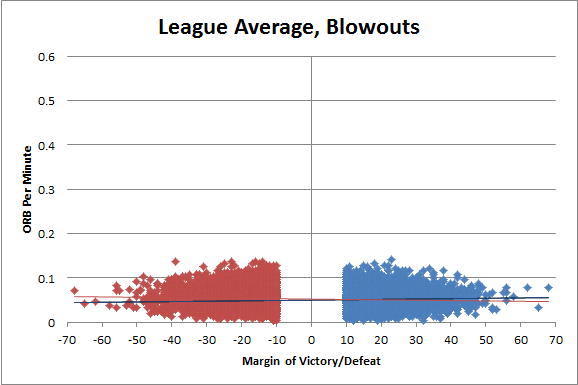
After thinking about how this hypothesis could be tested, I decided to look at the relationship between offensive rebounds per minute and Margin of Victory in “blowout” games (which I’ve arbitrarily set at 10+ points).  I chose offensive rebounds for a very specific reason: unlike defensive rebounds, they have virtually no correlation with winning.  While getting an offensive rebound is obviously better than not getting one, their strong correlation with missed shots cancels this out almost perfectly.  So let’s look at a simple scatter-plot for the entire league first.  Here are all team games since 1986:

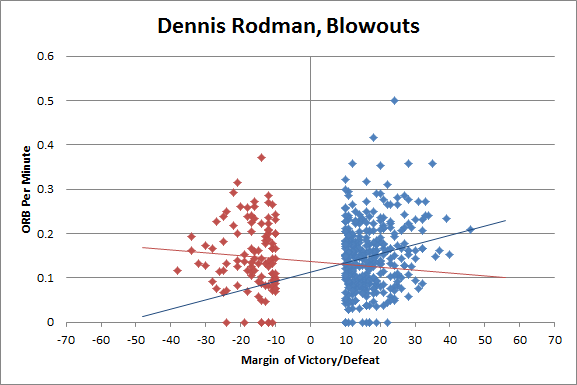
The red line is a trendline through just the blowout losses, and the blue is a trendline just through the blowout wins.  They are hard to make out because they are virtually flat: there does not seem to be a meaningful relationship between offensive rebounds per minute and total margin for either team in blowout situations.  Now let’s look at exactly the same graph, but just for Dennis Rodman:

We can clearly see upwardly sloping trendlines both in victory and defeat.  In other words, in blowout games, the bigger the blowout, the more offensive rebounds Rodman grabbed per minute, regardless of which side his team was on. [Perhaps the “X” is for “X-Factor”?]  This result is both consistent with and supportive of the theory: The wider the finishing margin, the more likely a game is to feature significant amounts of “junk” or “meaningless” time.  And the wider the finishing margin, the more rebounds Rodman grabbed.

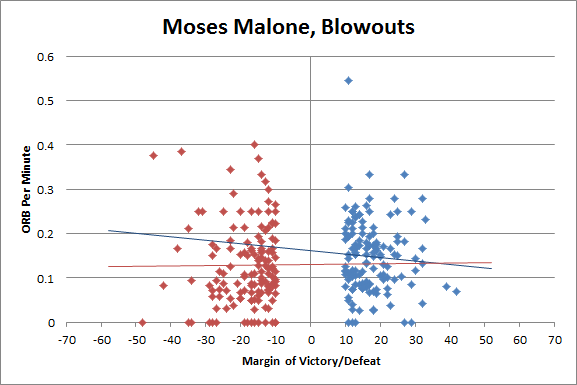
For comparison, let’s look at another great offensive rebounder and Hall of Famer, Moses Malone (from 1986 on):

Obviously, these trendlines aren’t increasing in either direction (in fact, they are both slightly decreasing).  They are both much flatter, and lack the prominent “X” shape that Rodman’s had: Moses Malone doesn’t appear to demonstrate any propensity to become more rebound-happy in “non-crunch” time.

While these sample-sizes are too small to prove anything on their own, if this proposed theory is one of the more plausible causes for our two provably extreme and independent effects, the data being consistent with and moderately supportive of the hypothesis could easily be enough to lend it considerable credence.

Analysis:

Trying to draw potential conclusions about causal factors based on indirect (Bayesian) analysis like this is always tricky.  First, you need to establish that your proposed theory, if true, really would be a plausible explanation (or significant contributing explanation) for your phenomena.  And second, it has to be the best explanation possible.  Meaning, your conclusion that z is the likely cause of x and y is entirely contingent on their not being a q that would be just as good of an explanation or better.  In the real world (outside the safety of contrived exam questions), this second condition is much harder to satisfy:  Even the most detailed studies, that include the most exhaustive considerations of conceivable factors, can be (and often are), scuttled by the tiniest failure of imagination.  So on that front, I don’t have much to say except that I’ve thought about potential causes of these anomalies for a while now and haven’t thought of anything better, yet.  [I won’t go into all of the details here, but since someone will probably bring it up if I don’t, I should note that I’ve looked into the theory that Rodman’s lack of tradeoff could be explained by his abnormally low usage rate (which I’ll discuss a bit more in section b).  Though this sounded promising on its face, the data didn’t back it up: the relationship between usage and rebounding tradeoff for both the league and Rodman himself is negligible.]  Of course, I would love to hear any other suggestions.

On the question of whether this explanation is plausible, I think so.  As I’ve said before, professional basketball is a game of very small margins: 3 points is the difference between a Ray Allen jumper dropping in or rolling out, yet 3 points per game is the difference between the 2011 Boston Celtics and the 2011 Houston Rockets, and 3 points of MOV differential is what separates Kobe Bryant from Delonte West.  I don’t think it would take that much intentional misconduct to shave several points off of a player’s MOV.  And if you so desired, playing in a lot of lopsided games—as Rodman did—would give you ample opportunity to do so without meaningful consequences in the W/L columns.

But could it help explain the trade-off anomaly? Though it relies on considerably more speculative reasoning, I find the theory highly plausible in this context as well:

First, I imagine that the tradeoff between offensive and defensive rebounding rates exists as the consequence of very basic strategic choices:  Imagine you’re a ball-boy and all you have to do is run out on the court and grab rebounds as efficiently as possible: you’d consistently run to the spot where you think the ball is most likely to go, wait there until the ball hit the rim, and then run wherever it actually goes.  But an actual player has many competing factors:  First, long before the shot is taken, he has to execute the offensive game-plan to maximize his team’s chances of scoring.  Then once the play is no longer in his control, he has to position himself to maximize all potential outcomes: cheating too much toward the basket might leave you out of position when the defense gets the ball and opening up a lane for a quick break, or prevent you from getting back into your half-court defensive position in time.  Similarly concerns exist on defense: being out of position could obviously open up a shot for your opponents, but could also hurt your team’s chances on the break, or leave you out of position for an effective transition after a made basket.

We don’t need to get into every gory detail of offensive and defensive strategy, but the main thing to notice is this: basketball is an extremely dynamic game, and the decisions you make have consequences all over the court.  And it’s not just rebound positioning, obviously, it’s everything: every movement you make in one direction or another affects where you can be two seconds later, which affects what kind of plans can be developed for 5 seconds later, and so on.  When you have a million little tradeoffs like this, the most efficient way to organize them is to group those that work together and complement each other, such as those that lean toward one side of the court or the other.

Of course, if you decided to eschew overall efficiency and go for every rebound regardless of the consequences, you would eliminate the constraining effect of, well, playing good basketball.

Indeed, this has always been the primary theoretical possibility for how Rodman managed to get so many rebounds on both ends of the floor and it’s by far the most common argument against his incredible rebounding stats: “Rodman didn’t care about anything else, all he did was go for rebounds.”   But that argument has a devastating response: Rodman’s freakish rebounding statistics couldn’t possibly be the product of bad play, because he played so damn good. As I put it in Part 2/4(b):

This is where “The Case for Dennis Rodman Was a Great Rebounder” and “The Case for Dennis Rodman” join paths: Showing that Rodman got a lot of rebounds without also showing that this significantly improved his teams proves neither that he was a great player nor that he was a great rebounder.

But there’s an opening here that I didn’t (openly) consider at the time: Perhaps Rodman did sub-optimally inflate his rebounding statistics—at least in non-critical situations—but played even more damn good than we imagined, and could thus actually get away with it.

Finally, I should be precise about what’s at stake here:  From his margin of victory differential alone, Rodman should rank right around the 98th percentile among full-time players.  Combining his MOV differential and his Win % differential (using the normal predictive method), moves him up to the mid-99th percentile.  And relying on his Win % differential alone would put him approximately in the top 99.98th.  Generally, about 5% of full-time players make the Hall of Fame, meaning this would put him in the 99th percentile of Hall of Famers:  In other words, he would deserve to be a shoo-in to make the Hall of Fame of the Hall of Fame. [If you’re interested in the statistical significance side, Rodman’s W% diff alone would put his p-value at <.0001, more than 3 times lower than Shaq’s.]

Indeed, if this theory—currently one of the only explanations for two independent virtually impossible statistical events, consistent with and supported by a cursory look at the data—is only partially true, and Rodman was at least partially a “selfish” player who cared more about padding his own rebounding stats than running up the score, not only would it imply that he was better than we thought, but that he should actually be All-Hall.

Monday: Was Dennis Rodman Better Than Michael Jordan?