I’ve been invited to participate in TrueHoop’s “Stat Geek Smackdown 2011” on ESPN.com. Unfortunately, I won’t actually get to smack any stat geeks, but I will get to pick NBA playoff series and compete with the likes of John Hollinger, David Berri, and Henry Abbot’s mom.
The rules are simple: each “expert” calls the winner of each series and the number of games (e.g., Spurs in 6)—5 points are awarded for each correct winner, with an additional 2 points for getting the length as well.
Most of the first round matchups have heavy favorites, so there isn’t too much disagreement on the panel about outcomes. But while researching my picks on Thursday night, I had some interesting findings that seemed a bit at odds with a lot of the others’ comments. So rather than going into the nitty-gritty of each series, I thought I’d summarize a few of these broader instances of divergence. Beware, a lot of this is preliminary stuff. I do think it is all on pretty solid footing, but there is much more to be done:
1. Form is overrated
At one point or another, nearly every expert quoted in this article cites a team’s recent good or bad performance as evidence that the team may be better or worse than their overall record would indicate. I’ve been interested in this question for a long time, and have looked at it from many different angles. Ultimately, I’ve concluded that there is no special correlation between late-season performance and playoff success. In fact, the opposite is far more likely.
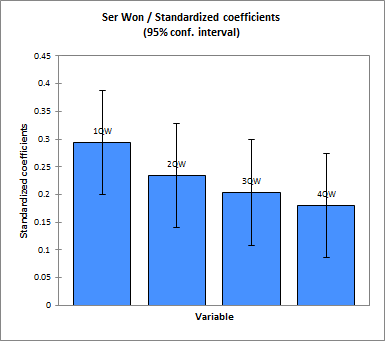
To examine this issue, I took the last 20 years of regular and post-season data, and broke the seasons down into 20 game quarters. I excluded the last 2 games of each season, which is mathematically more convenient and reduces a lot of tactical distortion (I also excluded games from the 1998-99 strike-shortened season). I then ran a number of regressions comparing regular and post-season performances of playoff teams. There are a lot of different ways to design this regression (should the regression be run on a game-by-game or series-by-series basis? etc.), but literally no permutation I could think of offered any significant support for the conventional approach of favoring recent results. For example, here are the results of a linear regression from wins by quarter-season to playoff series won (taller bars mean more predictive):
Aesthetically pleasing, no? As to why the later part of the season performs so poorly in these tests, it has been suggested that resting players and various other strategic incentives not to maximize winning may be the cause. That is almost certainly true to some extent, but I suspect it also has to do with the playoff structure itself: because of the drawn-out schedule, unvarying opponents, and high stakes, teams are better rested, better prepared, and more psychologically focused—not unlike they are at the beginning of each season.
2. Winning is underrated
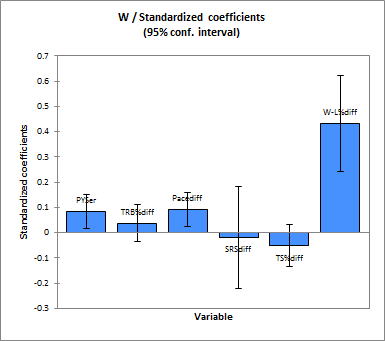
I’ve discussed this previously with respect to randomly-selected regular season games: Stat geeks pay too little attention to winning and focus too much on MOV, SRS, offensive/defensive efficiency, and other snazzy derivatives of the same basic quality. A better way to predict outcomes is to use a combination of winning and winning margins, with the latter being weighted slightly more heavily. Interestingly, however, the playoffs completely turn this situation on its head: The difference in regular-season winning percentage between two teams is much more predictive of individual playoff game outcomes than the difference between their margins of victory. This holds true for both home and away games (separately), as well as for series outcomes as a whole. For example, here is bar-graph comparing the predictive power of a number of “candidate” variables when combined in a logistic regression (taller bars are more predictive):
This comes from the same 20 year sample, with the regression to 1st round playoff series outcomes. I’ll talk about “PYS” and “pace” a little more below. The key variable here is “SRSdiff” (SRS, or Simple Rating System, is a popular variant on Margin of Victory that accounts for opponent strength). Note that it is close to zero.
So why the difference between the post-season and regular season? As I’ve said before, I think there’s a demonstrable and quantifiable skill to winning that is completely separate from scoring and allowing points. Intuitively, it makes sense to me that this skill would translate into the playoff environment just fine.
3. Playoff experience matters, at least on the road
Anecdotally, it always seemed to me that a lot of teams go deep in the playoffs one year, have mediocre regular seasons the next, only to go deep in the playoffs again anyway. To test this, I created a new variable I haphazardly named (PYS) or “Previous Year’s Series.” Basically, you get one point for each playoff series you appeared in, plus one for winning it all. So a team that misses the playoffs gets a 0, and the NBA champion gets a 5. I then calculated the difference between the two teams for each playoff series (the same as with each of the other variables), and tried including and testing it in several more regression models.
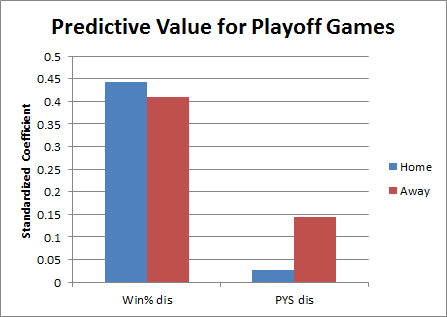
What I found is that “PYS” is a useful predictive stat (beyond the team’s winning percentage), but mostly only for away games: that is, teams who won more in the previous year’s playoffs tend to do better in playoff road games than their current season’s winning percentage (and other stats) would normally indicate. Here’s a side-by-side comparison (though note this comes from a regression that includes a few other variables as well):
4. Modeling 1st round series outcomes:
The beauty of analyzing first round series is that you can avoid the complications and pitfalls of calculating or simulating a bunch of results. In this case, I chose to do a logistic regression directly onto chances of winning the series. After much fiddling, I found that the most accurate and reliable model is relatively simple (which often turns out to be the case). It uses only 3 variables: W% disparity, PYS disparity, and pace disparity, with W% being by far the most important. For the serious math nerds out there, here is the Excel equation:
=1/(1+exp(-(-0.365+0.235*[pys]+13.235*[W-L%diff]+7.967E-02*[Pacediff])))
5. Pace is underrated
It continues to baffle me how so many sports statisticians go out of their way to purge “pace” from their models (e.g., Hollinger’s team efficiency stats are all “per 100 possessions”).
I’ve said this before and I’ll say it again: your chances of winning are necessarily a function of your reciprocal advantage per trade of possession AND the number of such trades you fit into each game. Indeed, pace turns out to be one of only two major variables that are still statistically significant to predicting both game and series outcomes even after accounting for win percentage.
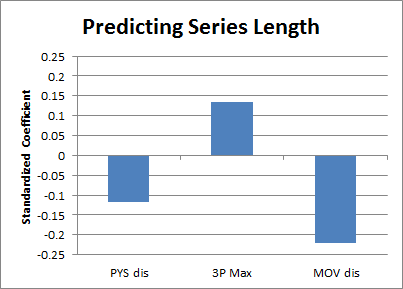
6. Series lengths favor Margin of Victory
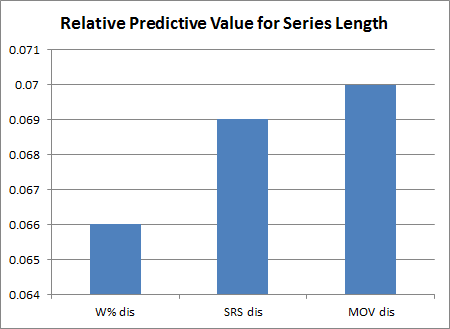
To me, this was probably the most interesting bit of info I’ve unearthed in any of my research in a long time. We should expect series lengths (e.g. 5 games, 6 games, etc.) to be mostly a function of the how big of a favorite the favorite is. All the research points to Win % as being the stronger predictive metric in the playoffs, but as it turns out, MOV is actually the best predictor of series length (the numbers for this chart came from 3 separate regressions that used each of these metrics independently):
Why this is, so far I can only speculate: MOV rewards dominance in victories, while Win% rewards ability to win by whatever means. So, in theory, it’s kind of surprisingly unsurprising that MOV would be better at predicting the likelihood of domination while W% would be better at predicting bottom-line results. But the crazy and fascinating part is that the independent skill of winning actually appears to transfer from individual games to complete series.
In any case, the best regression to series lengths that I could design used margin of victory disparity, PYS disparity, and one final element:
7. Lots of 3 point attempts = longer series
When either team shoots a lot of 3 pointers, the series takes longer on average, but ultimately with the teams winning at about the same rate. One of the benefits of doing regressions onto the entire series outcome instead of to individual game outcomes is that sometimes you can find these relationships that literally couldn’t exist if all the games were truly independent variables. The extra volatility of the 3-point shot ought to be black-boxed into their winning percentage (I discuss what I call “black-boxing” in a lengthy tangent here), but it’s not. The implications are ephemeral, but interesting: I think it might be indirect evidence that shooters really can run hot and cold for extended periods of time.
8. In a 7 game series, always pick 5 or 6 games:
From a purely statistical standpoint, 5 and 6 games are the only two reasonable choices: even for the closest and/or most lopsided matches, the range of expected outcomes is simply not large enough to justify predicting sweeps or game 7’s. The 72-win Bulls 1st round match had an expected series length of around 4.6, which is almost small enough to round down, but that’s as close as any series in 20 years has gotten. Of course, the strategy in the Stat Geek Smackdown might be a little different: being slightly contrarian can be the correct move for maximizing your chances of winning.
Update (5/1/11): An emailer correctly points out that, for Smackdown purposes (where you get no credit for being close), the mean series length isn’t what matters, but the mode. E.g., in the 72-win Bulls case, the expected series length could be 4.6 with 4 still being the most likely outcome.
It was sloppy of me to equate the result of the length-predicting model with the most likely outcome. But that is actually not the model I used to determine that 5 and 6 games are better picks than 4 and 7—it was strictly intended to identify the most influential variables. Rather, my research into most likely series lengths (which is still new and constantly changing) is based on a larger empirical investigation and some (comparatively) advanced simulations that attempt to correctly account for underlying error rates and for teams that are likely to be stronger on the road or in elimination games, etc. I may post some of these results when I’ve refined them a bit more, but I stand by my claims that 4 game picks are for suckers—even in the most lopsided series—and that the C.W. against picking home teams in 6 is misguided.
Just curious – did you test the predictive power of covariance terms in your regression? I would expect a whole lot of these variables to be strongly correlated.
Yes, it is a very important part of variable selection. The program I use for regressions includes covariance analysis in every output.
I think a lot of the focus on recent form this year is due to the crazy trade deadline player movement. The pre tradeline history for a number of playoff teams is somewhat irrelevant because they’re essentially putting out new teams.
Fascinating stuff. To what extent are these results sport specific, and to what extent do you think these claims can be extended to all sports (football, baseball, etc)?
[…] was, to some extent, inspired by the article by Benjamin Morris on his blog Skeptical Sports, where he suggests that to win playoff games in the […]
Great piece.
How is HCA not part of your series prediction model? How do we know the impact of win % isn’t in large part just reflecting home court advantage? (I realize you do find an independent effect in the individual game predictions since you did home and away separately.)
The impact of win% in the first-round series does reflect home court advantage in that model, by design. If there had been any series where the team with the worse record had HCA, I would have used a different model or modeled it separately.
“comparing the predictive power of a number of “candidate” variables when combined in a logistic regression”
I’m probably not understanding you right but just in case, when you include independent variables in the same regression model that tend to correlate with one another, it weakens the overall correlation of each variable with the dependent variable. In other words, using two more more independent variables which, as you said yourself, basically try to measure the same stuff, will screw it up for all of them.
I think a better approach (which you may actually be using if I’m not understanding you correctly) is to run separate regressions for each independent variable directly against the dependent variable and see how they stack up then.
Yes, I do run the regressions independently as well, but I’ll often run a version with all the candidate variables just for eyeballing the situation. If you have two versions of a similar variable and one comes out as *much* more important in the combined regression, that one will usually end up winning in the more accurate independent measurement also.
[…] momentum like that isn’t necessarily a harbinger of playoff doom (to the contrary, late-season form is often overrated by analysts when predicting which teams will rise or fall in the playoffs), but it is troubling […]
[…] Late season performance has almost no added correlation to playoff performance, and in fact, early season performance tends to be more influential on who wins any particular title. See the excellent work of the imitable Benjamin Morris for the backing on that. […]